_ROOT Version:Both 5 and 6
_Platform:Ubuntu 14-16-18
Compiler: Not Provided
Dear root experts,
I would like to make a polar graph which I don’t know if possible under root framework.
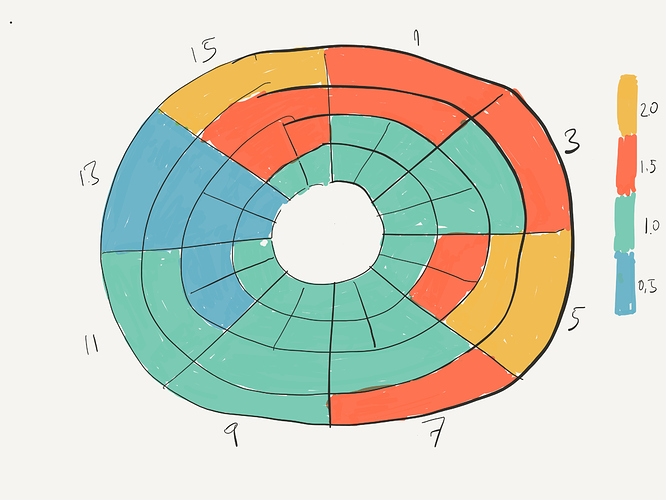
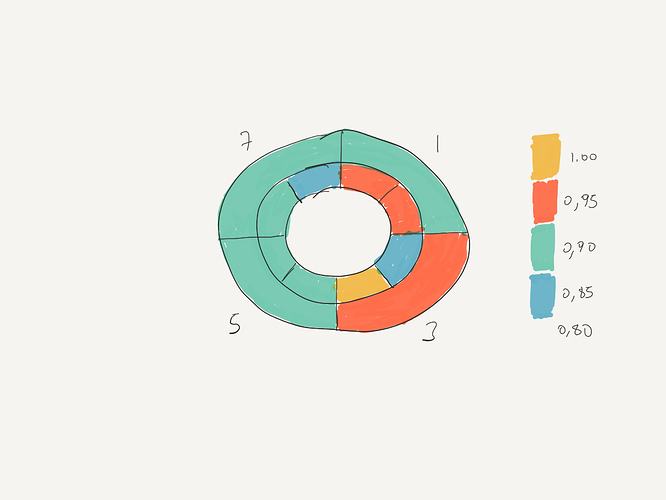
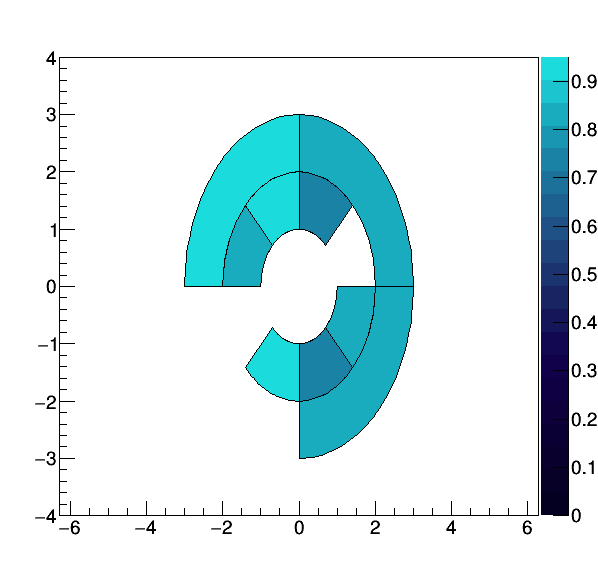
I just made a quick sketch of it and attached.
I will define histograms like
TGraphErrors* hist[4];
hist[i] = new TGraphErrors(16, x, y, ex, ey); for i=0,1
where double x[16]; and double y[16];
hist[j] = new TGraphErrors(8, x, y, ex, ey); for j=2,3
where double x[8]; and double y[8];
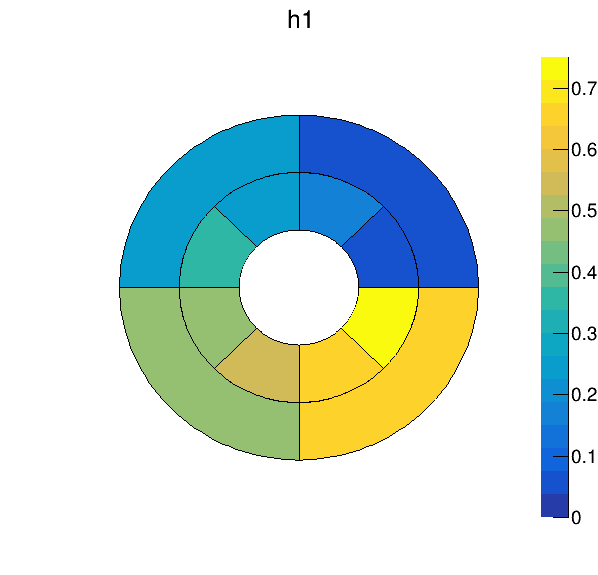
Polar graph will have 4 concentric circles and 16/8 division along the circle. Divisions will be labeled by numbers and not by angles.
I tried TGraphPolar instead of TGraphErrors, couldn’t do.
I tried TH2D and then fill x,y and then Draw->(“colzpol”) or Draw->(“pollego2z”)
I tried lots of other stuff too, all to no avail.
Is it possible to make a graph as shown in the sketch ? If possible, can you tell me how I can do it ? Just give me the recipe, I can do the rest.
Thanks