Hi,
I’m looking for the best suited plot type:
I have a simulation in which I rotate a device around 360° in 1° steps. At each step I measure a certain value (in my case efficiency). Now I’m thinking for the best plot how to depict that.
I’m thinking of a pie plot with 360° subdivisions but then I need a way to draw the parameter at each such a subdivision. Maybe color?
Is this doable with a pie chart?
Thank you!
TH1 can be plotted as pie charts. “option PIE”… but I am not sure that what you want.
The POL COL Option also for TH2 might be an other approach. It is difficult to tell what is the best.
In which kind of object are stored your data ?
Thank you!
At the moment I’m collecting data and it will just be an array of 360 elements.
The colz-option should be sufficient. Will try this out later!
I got my data now and was able to draw a pie chart. Is there a way to get rid of the labels? In my case I have 360 degrees and so 360 labels.
Got it:
pie->SetLabelFormat(“”);
I’ve some more questions:
At first I would like to draw a legend of the colors so one can get a feeling what the colors represent:
Hence, since I’ve rotated a device I would like to now where angle 0° is and where angle 360° is / respectively in my case -180° and 180° though both are the same 
But however I need to know where they are located. My code is:
Int_t angles[]={-180, -179, -178, .......... , 176, 177, 178, 179, 180};Double_t APD_first={ 5244, 5171, 5124, 5160, 5169, … 5123, 5210, 5126, 5234};
TPie *pie4 = new TPie(“APD1”, “APD1”, 361, APD_first);
pie4->SetRadius(.2);
// pie4->SetLabelsOffset(.01);
pie4->SetLabelFormat(“”);
pie4->Draw(“nol <”);
As you can see I’m using the number of degrees instead of the angles direct so I doubt it’s correct. Furthermore I don’t now how “nol <” is applied.
Thank you!
I changed the draw option to “nol” for the first one and “colz” for the second and got:
It seems that the angles are sorted mathematically positive -> angle 0° starts at y=0 at the right.
But the colors are a bit non-telling though both charts hold different values.
“nol” ? it is not a drawing option.
Aehm, ok. The line
" pie->Draw(“nol <”); "
on ROOT: TPie Class Reference looked like a drawing option.
Sorry but I do not see this line when I click on the URL you are referring to.
Oh I see you mean:
https://root.cern.ch/doc/master/classTPie.html#aa6236a893b18e2e1081392b3a5d99aa2
Yes that is to avoid the drawing of outlines when you draw a Pie chart
Sorry, there was something added to the URL by accident. It is:
https://root.cern.ch/doc/master/classTPie.html
Yes on this example the 4th pie chart has no outlines.
So what is your problem ?
Is there a small example you can provide to illustrate your question ?
At first thanks a lot for your support!
I’m looking for a better plot or draw option. The pie consists of 360 slices and each holds a certain value respectively represents a parameter. I would like to use “colz” or something similar to show how this parameter changes along the 360°.
At the moment the colors do not look like they are representing the values accordingly. It looks like they are only displaying a color gradient without any background information.
Here is the whole code:
#include “TGaxis.h”
#include “TCanvas.h”
#include <TGraphErrors.h>
#include <TStyle.h>
#include <TPie.h>
#include <TROOT.h>
#include <TFile.h>int anglescan()
{
TCanvas *c = new TCanvas(“c”,“canvas”,0,0,1200,700);
c->Divide(2,1);
TGraph2D *dt = new TGraph2D();
dt->SetTitle("APD ratio map; z / mm; x / mm; ");
TGraph2D *dz = new TGraph2D();
dz->SetTitle("APD ratio relative to mean; z / mm; x / mm; ");Int_t angles[]={-180, -179, -178, -177, -176, -175, -174, -173, -172, -171, -170, -169, -168, -167, -166, -165, -164, -163, -162, -161, -160, -159, -158, -157, -156, -155, -154, -153, -152, -151, -150, -149, -148, -147, -146, -145, -144, -143, -142, -141, -140, -139, -138, -137, -136, -135, -134, -133, -132, -131, -130, -129, -128, -127, -126, -125, -124, -123, -122, -121, -120, -119, -118, -117, -116, -115, -114, -113, -112, -111, -110, -109, -108, -107, -106, -105, -104, -103 -102, -101, -100, -99, -98, -97, -96, -95, -94, -93, -92, -91, -90, -89, -88, -87, -86, -85, -84, -83, -82, -81 -80, -79, -78, -77, -76, -75, -74, -73, -72, -71, -70, -69, -68, -67, -66, -65, -64, -63, -62, -61, -60, -59, -58, -57, -56, -55, -54, -53, -52, -51, -50, -49, -48, -47, -46, -45, -44, -43, -42, -41, -40, -39, -38, -37, -36, -35, -34, -33, -32, -31, -30, -29, -28, -27, -26, -25, -24, -23, -22, -21, -20, -19, -18, -17, -16, -15, -14, -13, -12, -11, -10 -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180};Double_t APD_first={ 5244, 5171, 5124, 5160, 5169, 5255, 5034, 5324, 5277, 5217, 5268, 5295, 5326, 5484, 5324, 5449, 5418, 5531, 5715, 5609, 5484, 5678, 5635, 5457, 5611, 5737, 5601, 5760, 5582, 5608, 5846, 5786, 5784, 5957, 5898, 5844, 5828, 5882, 5980, 6002, 6056, 5922, 5979, 6042, 5960, 5990, 6009, 5950, 6075, 5965, 5973, 5838, 5949, 5868, 5726, 5748, 5617, 5671, 5685, 5621, 5454, 5701, 5606, 5546, 5550, 5466, 5474, 5426, 5343, 5395, 5395, 5343, 5327, 5320, 5227, 5247, 5276, 5254, 5373, 5310, 5245, 5082, 4970, 5033, 4980, 5033, 5001, 4928, 5168, 4972, 5113, 5018, 5128, 5109, 5108, 5096, 5082, 5094, 5073, 5099, 4966, 4999, 4946, 5046, 5030, 4957, 4924, 4970, 4937, 4998, 4939, 4959, 4951, 4953, 4940, 5093, 4961, 4935, 4990, 4998, 4938, 4958, 4974, 4990, 5001, 5013, 5077, 4968, 4896, 4960, 5024, 4964, 4852, 5069, 4959, 5047, 4999, 4957, 5145, 5095, 5056, 5212, 5153, 5139, 5125, 4981, 5116, 4994, 4997, 5059, 5104, 5133, 4954, 5054, 5132, 5071, 5049, 5057, 5367, 5143, 5150, 5207, 5149, 5270, 5181, 5251 ,5160, 5180, 5231, 5277, 5227, 5259, 5275, 5127, 5200, 5206, 5252, 5250, 5211, 5343, 5330, 5438, 5402, 5389, 5426, 5534, 5431, 5592, 5650, 5630, 5680, 5669, 5664, 5696, 5643, 5862, 5674, 5923, 5721, 5804, 5890, 5925, 6021, 6075, 6075, 6058, 6128, 6723, 6244, 6099, 6202, 6086, 6240, 6245, 6122, 6257, 6102, 6068, 6176, 6311, 6311, 6154, 6331, 6212, 6238, 6231, 6237, 6181, 6187, 6176, 6167, 6119, 6319, 6321, 6298, 6318, 6380, 6306, 6330, 6413, 6330, 6435, 6377, 6419, 6503, 6561, 6426, 6376, 6311, 6461, 6440, 6466, 6393, 6435, 6503, 6403, 6390, 6361, 6444, 6319, 6278, 6235, 6313, 6238, 6282, 6344, 6255, 6311, 6208, 6236, 6194, 6284, 6287, 6362, 6281, 6332, 6237, 6345, 6203, 6422, 6409, 6365, 6383, 6439, 6440, 6383, 6298, 6374, 6450, 6356, 6450, 6343, 6326, 6357, 6427, 6470, 6366, 6296, 6160, 6408, 6227, 6173, 6156, 6261, 6043, 6282, 6209, 6136, 6147, 6106, 6113, 5998, 6006, 6002, 5894, 5877, 5847, 5825, 5784, 5825, 5840, 5819, 5826, 5806, 5837, 5715, 5749, 5765, 5553, 5598, 5614, 5519, 5547, 5658, 5635, 5577, 5454, 5410, 5524, 5432, 5388, 5342, 5390, 5563, 5281, 5240, 5283, 5257, 5158, 5097, 5220, 5148, 5192, 5133, 5203, 5176, 5238, 5123, 5210, 5126, 5234};
Double_t APD_second={ 4795, 4854, 4830, 4928, 4825, 4791, 4866, 4803, 4898, 4925, 4904, 4931, 5020, 5009, 5125, 5010, 5068, 5114, 5043, 5031, 5150, 5026, 5073, 5114, 5028, 5197, 5284, 5099, 5202, 5227, 5270, 5213, 5248, 5179, 5138, 5228, 5121, 5198, 5009, 5165, 5258, 5151, 5242, 5329, 5370, 5207, 5252, 5362, 5375, 5447, 5475, 5396, 5517, 5400, 5444, 5363, 5432, 5337, 5470, 5307, 5292, 5413, 5451, 5326, 5370, 5413, 5411, 5299, 5389, 5337, 5475, 5436, 5421, 5492, 5352, 5415, 5378, 5317, 5242, 5361, 5374, 5279, 5301, 5223, 5195, 5121, 5185, 5266, 5141, 5112, 5092, 5244, 5229, 5155, 5180, 5209, 5133, 5151, 5166, 5077, 5021, 4998, 5013, 5005, 4914, 5011, 4857, 4862, 4828, 4757, 4840, 4872, 4790, 4835, 4770, 4734, 4827, 4742, 4774, 4718, 4741, 4843, 4727, 4564, 4495, 4403, 4449, 4496, 4430, 4450, 4475, 4577, 4479, 4408, 4341, 4420, 4505, 4427, 4426, 4339, 4458, 4431, 4483, 4370, 4473, 4506, 4590, 4550, 4490, 4609, 4579, 4643, 4537, 4670, 4653, 4799, 4557, 4781, 4633, 4845, 4764, 4837, 4887, 4902, 4826, 5001, 4973, 5079, 4901, 4867, 4791, 4939, 4965, 4895, 4819, 4996, 4874, 4919, 4965, 4907, 5008, 5101, 5217, 5029, 5009, 5074, 5132, 5056, 5165, 5104, 5196, 5280, 5295, 5271, 5383, 5277, 5345, 5421, 5505, 5623, 5637, 5593, 5625, 5606, 5757, 5547, 5723, 5634, 5699, 5848, 5907, 5735, 5858, 5836, 5884, 5722, 5695, 5770, 5647, 5694, 5694, 5837, 5869, 5942, 5819, 5857, 5835, 5844, 5783, 5904, 5930, 6025, 5772, 6020, 6113, 6048, 6019, 6137, 6207, 6268, 6182, 6203, 6194, 6231, 6231, 6234, 6251, 6236, 6175, 6101, 6204, 6156, 6194, 6177, 6075, 6202, 6273, 6201, 6213, 6234, 6299, 6158, 6281, 6140, 6117, 6213, 6131, 6180, 6076, 6139, 6066, 6169, 6063, 6030, 6017, 6100, 6136, 6144, 6102, 6199, 6107, 6154, 6108, 6157, 6102, 6170, 6069, 6001, 6129, 6063, 6118, 6155, 6170, 6078, 6154, 6018, 6005, 5931, 5950, 5888, 5886, 5902, 5877, 5852, 5924, 5863, 5766, 5754, 5777, 5740, 5684, 5687, 5663, 5553, 5610, 5568, 5556, 5602, 5543, 5530, 5662, 5737, 5436, 5544, 5464, 5405,
5318, 5359, 5146, 5212, 5240, 5218, 5259, 5218, 5146, 5031, 5131, 5121, 5203, 5217, 5121, 5116, 4961, 4946, 5102, 5071, 5038, 4970, 4893, 4897, 4819, 4811, 4894, 4921, 4875, 4780, 4844, 4836, 4843, 4815, 4790};c->cd(1);
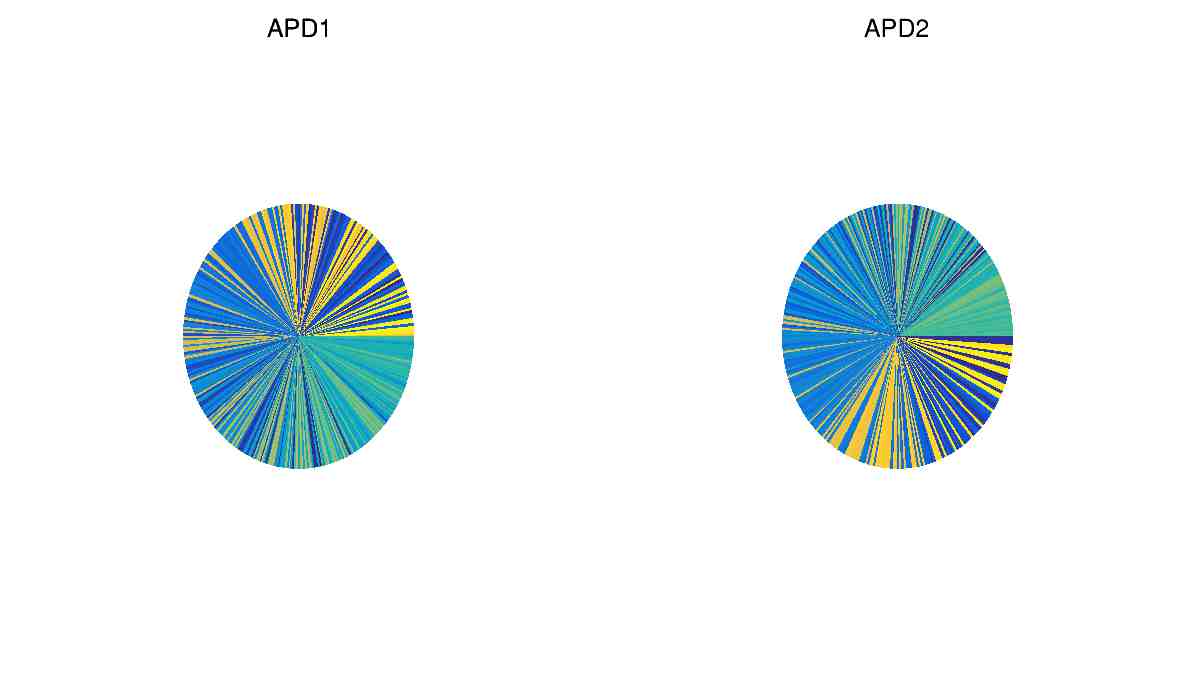
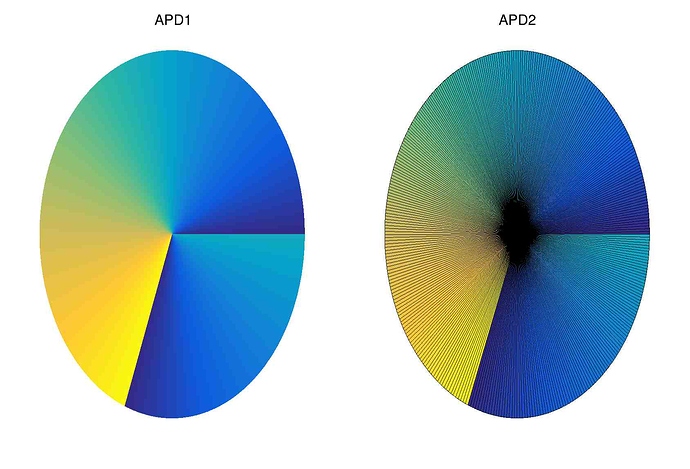
TPie *pie4 = new TPie(“APD1”, “APD1”, 361, APD_first);
pie4->SetRadius(.4);
// pie4->SetLabelsOffset(.01);
pie4->SetLabelFormat(“”);
pie4->Draw(“colz”);c->cd(2);
TPie *pie5 = new TPie(“APD2”, “APD2”, 361, APD_second);
pie5->SetRadius(.4);
// pie5->SetLabelsOffset(.01);
pie5->SetLabelFormat(“”);
pie5->Draw(“colz”);return 0;
}
Thanks for your example. I will try it and comme back to you.
You are using the option COLZ in when you draw your pie charts. But is option does not exist. The only available options are listed here:
https://root.cern.ch/doc/master/classTPie.html#aa6236a893b18e2e1081392b3a5d99aa2
That’s true - but I cannot display my needs with these options 
So I obviously need another type of plot. Which looks like a pie 
It is still not clear to me what “your needs” are . Can you point to some plot on the web looking like what you are looking for ?
That’s the thing, I’m looking for a convient plot to represent my results.
I’ll sketch what I did:
There is a fibre pointing towards a crystal and at the back of the crystal two APDs are attached. Everything is housed.
Now I rotated the fibre at its fixed location in 360 degrees and checked at each degree how much light is injected into each APD.
Hence, I want to sketch this. So I thought of displaying the rotation of the fibre as a pie chart and each of the 360 slices (which equal to the 360 degrees) represents the detected light of the APD at this degree.
Actually I’m thinking of using a 2D polar plot but transforming a xy plot into a proper “pie” plot seems to be too difficult for this task.
edit: Maybe it’s not that difficult as I can use the following:
x = r * cos * (Phi)
y = r * sin * (Phi)
r = 1
and z = APD_first[Phi] or APD_second[Phi]
Then I should be able to use a regular TH2F plot.
Will try this.
Yes may be a TH2 will be better. When you draw a pie chart the size of a slice is proportional to the value assigned to this slide (as a pie chart should be). I am not sure that’s what you want according to the description you are giving. At the end you may need to produce your own specific plot using low level basic primitives like TArc,
