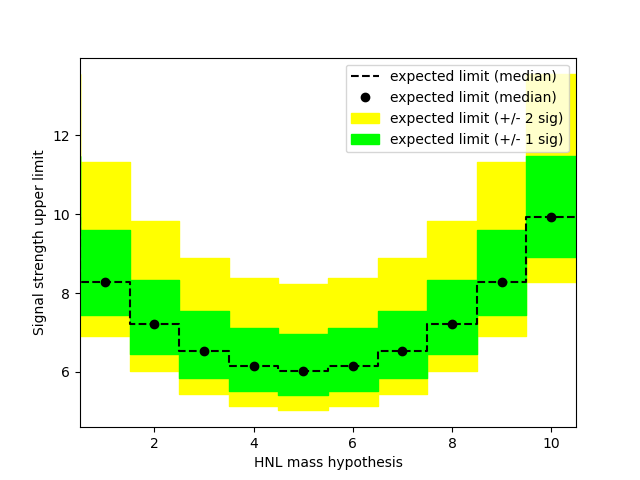
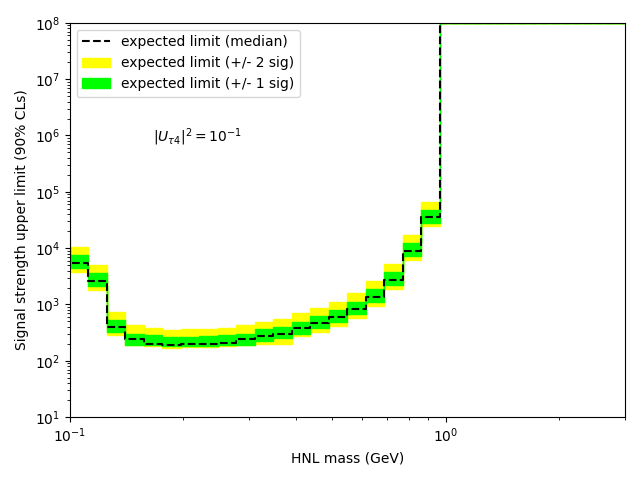
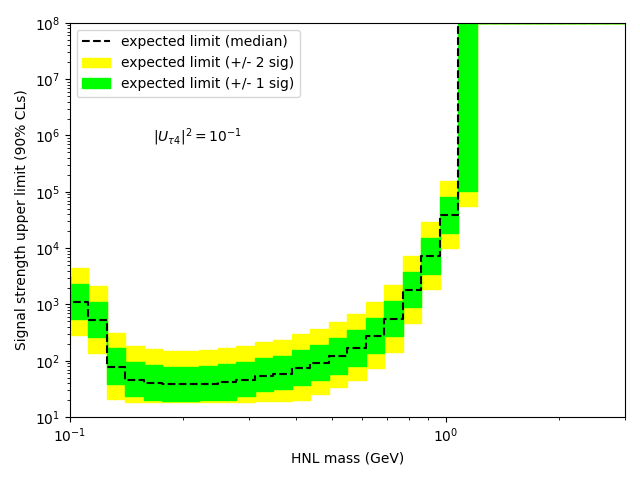
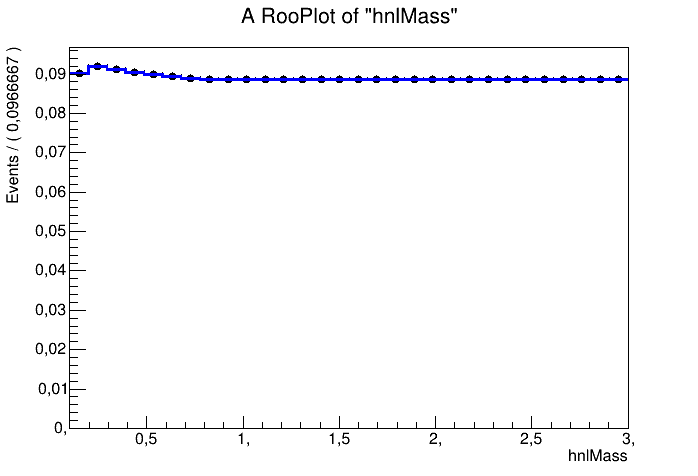
Hi, thanks for sharing the script!
I see that your dataset has the “hnlMass” as the observable. So when we talk about HNL mass here, we have to distinguish two different variables. On one side there is the observed mass, on the other side there is the HNL mass that you set in you model right. However, I don’t wee the HNL mass model parameter in your script.
I took a look at the lines 240 to 250 in your script, where the signal model is defined:
obs = ROOT.RooArgSet()
obs.add(hnlMass)
hist_temp = ROOT.TH1D("hist","hist",30,0.1,3.)
bins = np.linspace(0.1,3.,31)
array_binned, _ = np.histogram(data,bins,weights=data_weights)
hist = array2hist(array_binned,hist_temp)
dataHist = ROOT.RooDataHist("hist","hist",obs,hist)
sigPDF = ROOT.RooHistPdf("histpdf","histpdf",hnlMass,dataHist,0)
nsig = ROOT.RooRealVar("nsig", "nsig", 0, -10, len((data)))
sig_norm = ROOT.RooExtendPdf("sig_norm", "sig_norm", sigPDF, nsig)
Put in words, you are creating the template from the signal model from “data”, which is:
data = np.concatenate((signal,bg))
So one thing that’s probably wrong is that you consider the background in the signal template. The other problem is that you take the shape from the signal template from the data that you fit the template to. So something is fishy there: you double count your background and you fit the data to a template defined by the data.
From your original question…
My question is: how do I get the upper limit (and corresponding +/- 1 and 2 sigma bands) as a function of the HNL mass?
…I thought that what you had was a model parametrized in the HNL mass, so you can get an upper limit for each probed mass. But this would also mean that you need a separate signal template for each mass value, possibly interpolating between them. I don’t understand how you can’t have a parametrized signal model in your script.
So basically you are fixing the mass to the mass observed in the data, but I don’t think that this is what you ultimately want to do 
I hope this gives you some ideas on what you need to adjust in your fit!
Cheers,
Jonas
 . It differs from a standard “bump hunt” as a function of the invariant mass for instance, because here the signal parameter is different for each bin, while in a classic bump hunt you fix the signal mass (the parameter) and scan the invariant mass (the observable). Ok, so now, what should I change for this to make sense?
. It differs from a standard “bump hunt” as a function of the invariant mass for instance, because here the signal parameter is different for each bin, while in a classic bump hunt you fix the signal mass (the parameter) and scan the invariant mass (the observable). Ok, so now, what should I change for this to make sense?