Two scales defined by a function

Newbie
1

ROOT Version: 6.30/04
Platform: Windows10
Compiler: Precompiled, downloaded from official site

Hello everyone!

I’m trying to do draw a histogram with two axis. I have checked the twoscales example and the TGaxis reference page and I did a simple example.

From the TGaxis reference page:

It should be noted that func is not defined in the user’s coordinate space, but in the new TGaxis space. If x is the original axis, w the new axis, and w = f(x) (for example, f is a calibration function converting ADC channels x to energy w), then func must be supplied as f^{-1}(w).

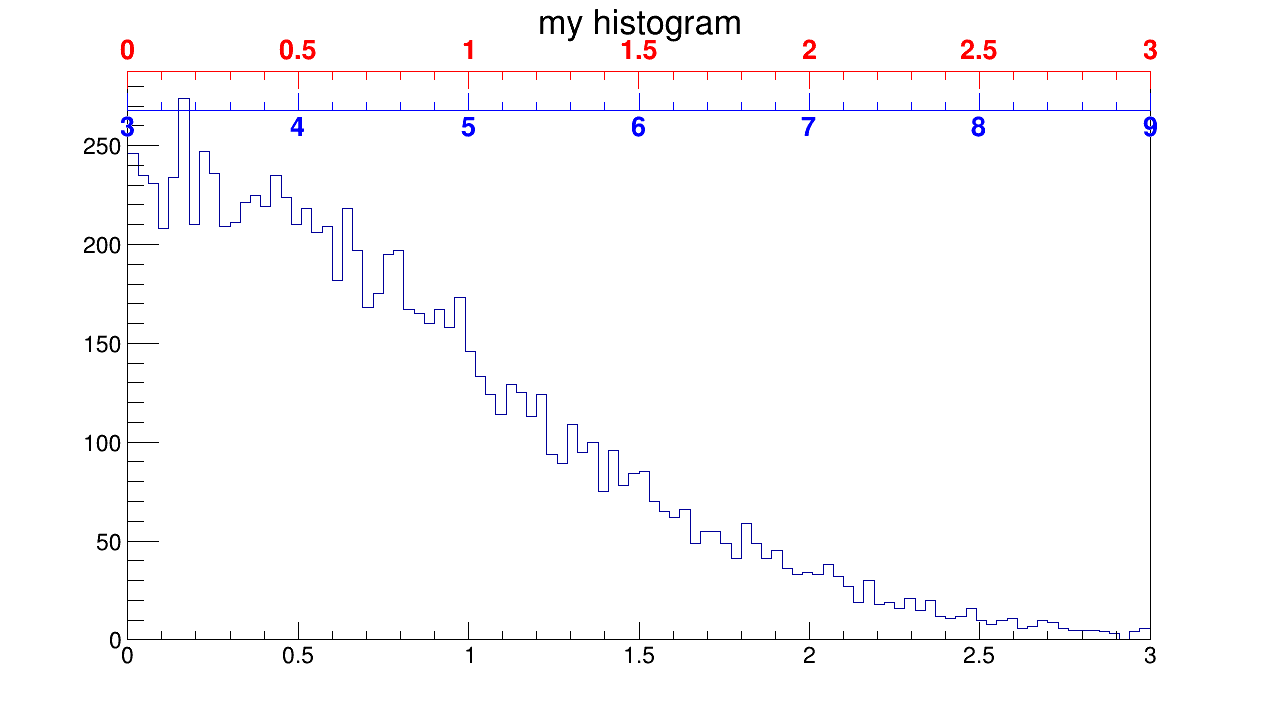
I want to do exactly this, draw my second axis on the top and do a linear scale, so it will be an energy calibrated axis and my original axis on the bottom will contain the ADC channel values.

For simplicity assume that my calibration looks like this: w = 2*x+3 (where x means channel, w means energy) so the func which must be supplied: func = f^{-1}(w)=(w-3)/2

My implementation in the code:

// Linear scaling function
    auto scalingFunction = new TF1("scalingFunction", "(x-[0])/[1]", 0, 3);
    scalingFunction->SetParameter(0, 3);
    scalingFunction->SetParameter(1, 2);

With this scaling on the [0,3] channel range I should get [2*0+3 = 3,2*3+3 = 9] on my red axis on top. However I simply get a [0,3] axis identical to the original (colored red).

I can still achieve my goal if I compute the limits of the desired axis using my scaling function (shown in blue offset from top) so I manually set wmin = 3, wmax = 9.

Did I misunderstand something about the creation of axis using a function? The quoted section about ADC channel to energy conversion suggests this linear function should be usable. I’ve tried to write my linear function directly (x-3)/2 as well, not with [0] & [1] parameters, but that didn’t help either.

I do not really now where is my problem but I noticed that it doesn’t matter which function do I use my limits will remain [0,3] and my tickmarks will scale (I’ve tried the provided examples which use -x, exp(x), log10(x)). But I believe this is not the expected behaviour based on this quote:

Instead of the wmin,wmax arguments of the normal definition, the name of a TF1 function can be specified. This function will be used to map the user coordinates to the axis values and ticks.

#include "TCanvas.h"
#include "TStyle.h"
#include "TH1.h"
#include "TF1.h"
#include "TGaxis.h"

void axisTest()
{
    TCanvas *c1 = new TCanvas("c1", "histo with different scales", 600, 400);

    // create/fill draw h1
    gStyle->SetOptStat(kFALSE);
    TH1F *h1 = new TH1F("h1", "my histogram", 100, 0, 3);
    h1->FillRandom("gaus", 1e4);
    h1->Draw();
    c1->Update();

    // Linear scaling function
    auto scalingFunction = new TF1("scalingFunction", "pol1", 0, 3);
    scalingFunction->SetParameter(0, 3);
    scalingFunction->SetParameter(1, 2);

    // draw an axis on the top
    TGaxis *axis = new TGaxis(gPad->GetUxmin(), gPad->GetUymax(),
                              gPad->GetUxmax(), gPad->GetUymax(), "scalingFunction", 510, "-L");

    // draw manual axis with manual limits with an offset then color it blue
    TGaxis *axis2 = new TGaxis(gPad->GetUxmin(), gPad->GetUymax()-20,
                               gPad->GetUxmax(), gPad->GetUymax()-20, 1, 4.12, 510, "+L");


    axis->SetLineColor(kRed);
    axis->SetLabelColor(kRed);

    axis2->SetLineColor(kBlue);
    axis2->SetLabelColor(kBlue);

    axis->Draw();
    axis2->Draw();
}

Thank you in advance!

twoAxis
twoAxis1278×711 7.23 KB

2

Dear @SRLeX ,

Thanks for reaching out to the forum! I am consulting with @couet to understand your situation better. We will reach back to you as soon as possible.

Cheers,
Vincenzo

3

Thank you in advance!

Minor correction to exactly reproduce my figure:
I forgot to update my example code in the original post (it uses wmin = 1, wmax = 4.12) and I cannot edit it now unfortunately. So as I said in the text I manually set wmin = 3, wmax = 9, that translates to code like this:

// draw manual axis with manual limits with an offset then color it blue
TGaxis *axis2 = new TGaxis(gPad->GetUxmin(), gPad->GetUymax()-20,
                               gPad->GetUxmax(), gPad->GetUymax()-20, 3, 9, 510, "+L");

I would also appreciate if you could mention to him my other topic TRatioPlot confidence bands - limiting, asymmetry, which I have not received a reply to for some time.

If you need further clarification about my problems, feel free to ask!

Cheers,
Lex

4

This functionality behaves like a log scale. When you draw an axis with a function, the tick marks are positioned according to this function but the labels remain what you gave. lie in log scale.

5

Thanks for your answer! If I understand you correctly this means that when I define my function e.g.

auto scalingFunction = new TF1("scalingFunction", "pol1", 0, 3);

my label limits will be [0,3] and in between the ticks will scale linearly. If I switch to log, exp, pol2 etc. limits stay, ticks scale according to these functions. I’ve tested this now and I think this functionality works fine.

I previously wrongly thought that If I supply my calibration parameters (a = 2, b = 3) as I presented in my original post then it should convert that [0,3] range to the [3,9] range and do a linear scale with the tickmarks, based on this section in the TGaxis reference page:

It should be noted that func is not defined in the user’s coordinate space, but in the new TGaxis space. If x is the original axis, w the new axis, and w = f(x) (for example, f is a calibration function converting ADC channels x to energy w), then func must be supplied as f^{-1}(w).

But now I realize this does not care about parametrization of the function, only the type of function. And naturally the inverse of a linear is linear regardless of the values of a and b where y = a*x+b (the 2 given limits uniquely define the function anyway). Please correct me if I’m wrong.

My followup question:
What if I have a quadratic (pol2) or higher order polynomial function?

If I use pol2, pol3, pol4 etc. functions I get the same tick scaling for all of them. If I give 2 calibrated limits and say I have pol2 that’s not enough to properly scale the ticks in between (2 points doesn’t even uniquely define a pol2 function) and as far as I know the scaling does not care about my parameter inputs.

Thank you in advance!

6

I made this example:

{
   auto c1 = new TCanvas("c1","Examples of Gaxis",10,10,700,500);

   TF1 *f0 = new TF1("f0","sqrt(x)",2,9.5);
   TGaxis *A0 = new TGaxis(0.1, 0.1, 0.9, 0.1, "f0", 1010, "");
   A0->SetTitle("f0 = sqrt(x)");
   A0->Draw();

   TF1 *f1 = new TF1("f1","x",-9,9);
   TGaxis *A1 = new TGaxis(0.1, 0.2, 0.9, 0.2, "f1", 1010, "");
   A1->SetTitle("f1 = x ");
   A1->Draw();

   TF1 *f2 = new TF1("f2","-x",-9,9);
   TGaxis *A2 = new TGaxis( 0.1, 0.3, 0.9, 0.3, "f2", 1010, "");
   A2->SetTitle("f2 = -x ");
   A2->Draw();

   auto f3 = new TF1("f3", "3*x+2", -9, 9);
   TGaxis *A3 = new TGaxis( 0.1, 0.4, 0.9, 0.4, "f3", 1010, "");
   A3->SetTitle("f3 = 3*x+2 ");
   A3->Draw();

   auto f4 = new TF1("f4", "pol1", -9, 9);
   f4->SetParameter(0, 3);
   f4->SetParameter(1, 2);
   TGaxis *A4 = new TGaxis( 0.1, 0.5, 0.9, 0.5, "f4", 1010, "");
   A4->SetTitle("f4 = pol1 with parameters 3 and 2 ");
   A4->Draw();

   auto f5 = new TF1("f5", "-3*x+2", -9, 9);
   TGaxis *A5 = new TGaxis( 0.1, 0.7, 0.9, 0.7, "f5", 1010, "");
   A5->SetTitle("f5 = -3*x+2 ");
   A5->Draw();

   auto f6 = new TF1("f6", "pol1", -9, 9);
   f6->SetParameter(0, -3);
   f6->SetParameter(1, 2);
   TGaxis *A6 = new TGaxis( 0.1, 0.8, 0.9, 0.8, "f6", 1010, "");
   A6->SetTitle("f6 = pol1 with parameters -3 and 2 ");
   A6->Draw();

   auto c2 = new TCanvas("c2","Examples of Gaxis",750,10,700,500);
   f6->Draw(); f6->SetLineColor(kBlue);
   f5->Draw("same");
}

As you can see the linear function f1 = x does not change the tick marks so doesn’t f3 = 3x+2. Same for f4 = pol1 with par 3 & 2. They are all linear with positive slope.

f2 and f5 have a negatove slope with invert s the label, but ticks are linear as they should.

f6 should behave à f5 … but it does not ! it is just like the SetParameter does not act on pol1 … it is confirmed by the 2nd canvas on which f5 and f6 are drawn.
f6 has a positive slope.

EDIT: indeed the parameters are not in the right order in this macro (see next post)

7

They are equal, you just didn’t set the parameters in the correct order.

polN: A polynomial of degree N, where N is a number between 0 and 9: f(x) = p0 + p1*x + p2*x2 +...

So you should write

f6->SetParameter(0,2);
f6->SetParameter(1,-3);

instead the other way around. And you will get the expected behaviour, sign of the first order matters (negative invert labels), but the actual value of [0], [1] parameter does not. (You can really nicely see this with your code after you correct the ordering.)

And this is fine with pol1, exp(x), log(x) since the two limits you manually compute (e.g. [0;3] range changes to [2;11] when you use f3=3x+2) will uniquely define the function (even without giving the actual parameters), the ticks between just have to run like the given function.

But my question is about what happens with more complex functions? E.g. pol2 is not uniquely defined by the two limits. So I’ve modified your code to check and everything looks fine. The parameters which you set do matter as expected.

{
   auto c1 = new TCanvas("c1", "Examples of Gaxis", 10, 10, 700, 500);
   auto f1 = new TF1("f1", "x", 0, 9);
   TGaxis *A1 = new TGaxis(0.1, 0.1, 0.9, 0.1, "f1", 1010, "");
   A1->SetTitle("f1 = x ");

   auto f2 = new TF1("f2", "pol2", 0, 9);
   f2->SetParameter(0, 2);
   f2->SetParameter(1, 3);
   f2->SetParameter(2, 4);
   TGaxis *A2 = new TGaxis(0.1, 0.5, 0.9, 0.5, "f2", 1010, "");
   A2->SetTitle("f2 = 2+3*x+4*x*x ");

   auto f3 = new TF1("f3", "pol2", 0, 9);
   f3->SetParameter(0, 10);
   f3->SetParameter(1, 8);
   f3->SetParameter(2, 2);
   TGaxis *A3 = new TGaxis(0.1, 0.9, 0.9, 0.9, "f3", 1010, "");
   A3->SetTitle("f3 = 10+8*x+2*x*x");

   A1->Draw();
   A2->Draw();
   A3->Draw();
}

scaling
scaling898×645 13.5 KB

I was a bit confused in the beginning, but after all this discussion I think I have a better understanding. Thank you everyone!

Cheers,
Lex

8

Oops … you are right … ! sorry for that, I messed up the parameters.