I want to plot a 2 dimensional histogram (TH2D) focusing on the range 0.9-1.1 (by setting the z axis range).
I found out, that bins with values above 1.1 are drawn with the palette top color, but bins with values below 0.9 are drawn with white, not the palette bottom color. What I would like to get is empty (zero) bins drawn with white, but bins with values 0 < v < 0.9 to be drawn with some other color (the palette bottom color would be the best).
Is it possible?
You can define your own contour levels, see http://root.cern.ch/root/html/TH1.html#TH1:SetContour
And you can define your own color palette, see http://root.cern.ch/root/html/TStyle.html#TStyle:SetPalette and http://root.cern.ch/root/html/TColor.html
Something like:
Int_t colors[] = {0, 1, 2, 3, 4, 5, 6}; // #colors >= #levels - 1
gStyle->SetPalette((sizeof(colors)/sizeof(Int_t)), colors);
// #levels <= #colors + 1 (notes: +-1.79e308 = +-DBL_MAX; +1.17e-38 = +FLT_MIN)
Double_t levels[] = {-1.79e308, 1.17e-38, 0.90, 0.95, 1.00, 1.05, 1.10, 1.79e308};
My2DHisto->SetContour((sizeof(levels)/sizeof(Double_t)), levels);
My2DHisto->Draw("colz");
also:
Hi,
I’m not sure if I was clear enough… or maybe I don’t understand the answer.
I believe I know how to set the palette (at least the way it is demonstrated in root.cern.ch/drupal/content/how- … or-palette). I’m not sure about the levels -1.79e308 and 1.10 in Pepe’s example - this doesn’t seem to work for me.
My histogram looks like this
TH2D * h = new TH2D("h", "", 10, 0, 10, 10, 0, 10);
h->SetBinContent(5, 7, 1.20); //this bin is drawn with color corresponding to palette
// level 1.0 (maximum), and I like it
h->SetBinContent(5, 6, 1.05);
h->SetBinContent(5, 5, 1.00);
h->SetBinContent(5, 4, 0.95);
h->SetBinContent(5, 3, 0.80); //this bin however is invisible, while I would like to
// see it
h->GetZaxis()->SetRangeUser(0.9, 1.1);
h->Draw("colz");See here , how the COL option is working.
Define your own color palette and contour levels AND remove the line:
h->GetZaxis()->SetRangeUser(0.9, 1.1);
BTW. In my example code, “{-1.79e308, 1.17e-38, 0.9, …}” means that everything between -DBL_MAX and +FLT_MIN (i.e. everything below +FLT_MIN) should be painted with the first color (i.e. colors[0] = 0 = “white”) and then everything between +FLT_MIN and 0.9 should be painted with the second color (i.e. colors[1] = 1 = “black”) and finally “{…, 1.10, 1.79e308}” means that everything between 1.1 and +DBL_MAX (i.e. everything above 1.1) should be painted with the last color (i.e. colors[6] = 6 = “pink”). Well, instead of 1.17e-38 (+FLT_MIN) you can also simply put 0.0 if you like it more. And instead of -1.79e308 you could use something like “(My2DHisto->GetMinimum() - 1)”, while instead of +1.79e308 you could use something like “(My2DHisto->GetMaximum() + 1)”. Just make sure that the “levels” are in increasing order.
Ok, I’m getting this. However there’s still one more problem: I’d like to display the actual palette (which is drawn with “colz” option) showing only range of 0.9-1.1. This is why I used SetRangeUser() function. What I get with your code is nice histogram, but the palette starts from zero, so 0.9-1.1 range on the palette is very small…
Maybe Olivier knows any neat solution … I can give you a brutal hack only (I’m not sure if the “statistics box” contains all correct values for the “full” histogram or maybe some are for the “user range” only) …
{
Int_t colors[] = {0, 1, 2, 3, 4, 5, 6}; // #colors >= #levels - 1
gStyle->SetPalette((sizeof(colors)/sizeof(Int_t)), colors);
// #levels <= #colors + 1 (notes: +-3.4e38 = +-FLT_MAX; +1.17e-38 = +FLT_MIN)
Double_t levels[] = {-3.4e38, 1.17e-38, 0.90, 0.95, 1.00, 1.05, 1.10, 3.4e38};
TH2D *h = new TH2D("h", "", 10, 0, 10, 10, 0, 10);
h->SetContour((sizeof(levels)/sizeof(Double_t)), levels);
h->SetBinContent(5, 7, 1.20);
h->SetBinContent(5, 6, 1.05);
h->SetBinContent(5, 5, 1.00);
h->SetBinContent(5, 4, 0.95);
h->SetBinContent(5, 3, 0.80);
TH2D *h_z = new TH2D(*h); // create a "copy"
h_z->GetZaxis()->SetRangeUser(0.89, 1.11); // ... set the range ...
h_z->Draw("z"); // draw "axes", "color palette", "statistics box"
h->Draw("col same"); // draw the "contents"
}
May be:
{
TH2D * h = new TH2D("h", "", 10, 0, 10, 10, 0, 10);
h->SetBinContent(5, 7, 1.20); //this bin is drawn with color corresponding to palette
// level 1.0 (maximum), and I like it
h->SetBinContent(5, 6, 1.05);
h->SetBinContent(5, 5, 1.00);
h->SetBinContent(5, 4, 0.95);
h->SetBinContent(5, 3, 0.80); //this bin however is invisible, while I would like to
// see it
h->DrawClone("col");
h->SetMaximum(1.1);
h->SetMinimum(0.9);
h->Draw("colz same ");
}
Olivier, after trying your code, I have the impression that the “lowest” and the “highest” rectangles have wrong colors (these colors come from the “original / full histogram scale” color palette / contours, not from the new ones created by setting the “user range”).
That would mean that the parts of the histogram “contents” that are outside of the “user range” are drawn with wrong colors.
In my example, I “enforce” the color palette and contour levels and they do not change after one sets the “user range”.
hmm … yes may be it need to be refine a bit… but I think that’s the way to go.
An improved / simplified version of my code …
{
Int_t colors[] = {0, 1, 2, 3, 4, 5, 6}; // #colors >= #levels - 1
gStyle->SetPalette((sizeof(colors)/sizeof(Int_t)), colors);
// #levels <= #colors + 1 (notes: +-3.4e38 = +-FLT_MAX; +1.17e-38 = +FLT_MIN)
Double_t levels[] = {-3.4e38, 1.17e-38, 0.90, 0.95, 1.00, 1.05, 1.10, 3.4e38};
TH2D *h = new TH2D("h", "", 10, 0, 10, 10, 0, 10);
h->SetContour((sizeof(levels)/sizeof(Double_t)), levels);
h->SetBinContent(5, 7, 1.20);
h->SetBinContent(5, 6, 1.05);
h->SetBinContent(5, 5, 1.00);
h->SetBinContent(5, 4, 0.95);
h->SetBinContent(5, 3, 0.80);
h->DrawClone("col");// draw "axes", "contents", "statistics box"
h->GetZaxis()->SetRangeUser(0.89, 1.11); // ... set the range ...
h->Draw("z same"); // draw the "color palette"
}
This looks very well! Thank you very much!
The only strange thing that happens is the top part of the palette bar going to the top of the picture, regardless of the palette size. But I managed to overcome this by removing the last entry in
Double_t levels[] = {-3.4e38, 1.17e-38, 0.90, 0.95, 1.00, 1.05, 1.10, 3.4e38};
since the values above the range set are plotted correctly by default.
Thank you again!
You’re right. One can easily overcome the error in palette’s size if one does not define the “upper limit” (I didn’t realize that up to now). I wonder if this bug could be fixed in the ROOT’s source code?
Well, while playing with this issue, I discovered another problem … if one adds more colors than “really needed” … one gets weird behavior of the palette … try each of:
Int_t colors[] = {0, 1, 2, 3, 4, 5, 6};
Int_t colors[] = {0, 1, 2, 3, 4, 5, 6, 7};
Int_t colors[] = {0, 1, 2, 3, 4, 5, 6, 7, 8};
Int_t colors[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
with:
Double_t levels[] = {-3.4e38, 1.17e-38, 0.90, 0.95, 1.00, 1.05, 1.10};
(Looking at some of my “old macros”, I can clearly see now that I’d already been fighting with “proper” assignment between colors and contours in some plots, but I forgot to report it.)
Hi,
I ended up with the following code:
#include <TH2D.h>
#include <TColor.h>
#include <TStyle.h>
#include <TCanvas.h>
using namespace std;
void paleta() {
//palette settings - completely independent
const Int_t NRGBs = 6;
const Int_t NCont = 999;
Double_t stops[NRGBs] = { 0.00, 0.1, 0.34, 0.61, 0.84, 1.00 };
Double_t red[NRGBs] = { 0.99, 0.0, 0.00, 0.87, 1.00, 0.51 };
Double_t green[NRGBs] = { 0.00, 0.0, 0.81, 1.00, 0.20, 0.00 };
Double_t blue[NRGBs] = { 0.99, 0.0, 1.00, 0.12, 0.00, 0.00 };
TColor::CreateGradientColorTable(NRGBs, stops, red, green, blue, NCont);
gStyle->SetNumberContours(NCont);
gStyle->SetOptStat(0);
//here the actually interesting code starts
const Double_t min = 0.9;
const Double_t max = 1.1;
const Int_t nLevels = 999;
Double_t levels[nLevels];
for(int i = 1; i < nLevels; i++) {
levels[i] = min + (max - min) / (nLevels - 1) * (i);
}
levels[0] = 0.01;
// levels[0] = -1; //Interesting, but this also works as I want!
TCanvas * c = new TCanvas();
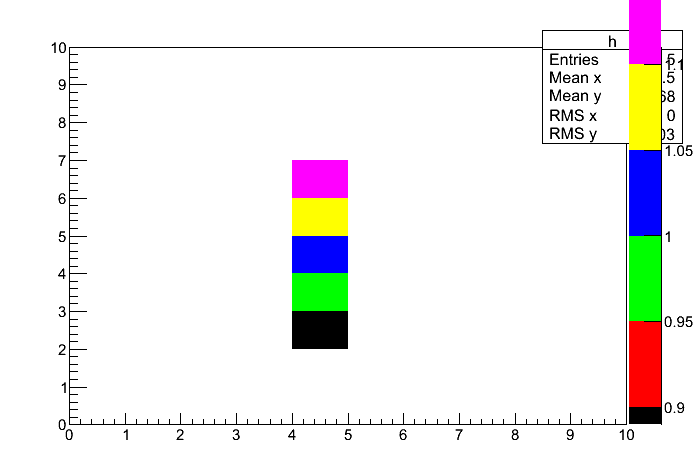
TH2D *h = new TH2D("h", "", 10, 0, 10, 10, 0, 10);
h->SetContour((sizeof(levels)/sizeof(Double_t)), levels);
h->SetBinContent(5, 7, 1.20);
h->SetBinContent(5, 6, 1.05);
h->SetBinContent(5, 5, 1.00);
h->SetBinContent(5, 4, 0.95);
h->SetBinContent(5, 3, 0.80);
h->DrawClone("col text");// draw "axes", "contents", "statistics box"
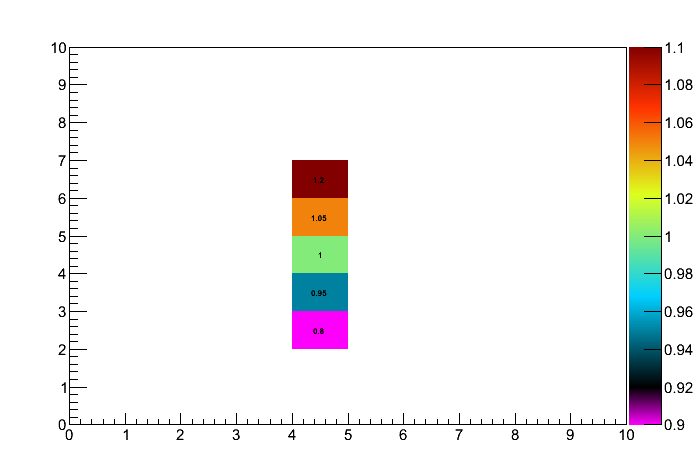
h->GetZaxis()->SetRangeUser(min, max); // ... set the range ...
h->Draw("z same"); // draw the "color palette"
c->SaveAs("c.png");
}Result:
What I found out, that the tricks with -3.4e38 and 1.17e-38 numbers are not really necessary. I can use the standard smooth palette without any modifications, the only trick is setting [color=#00FF00]level[0][/color] to something below [color=#00FF00]min[/color] (and below the minimal value I want to see on the plot). I see no need to use different color for values outside the [min, max] range, it’s usually obvious (at least in my case).
However, the behaviour is quite funny, since the code works nicely when I set [color=#00FF00]level[0][/color] below 0 - the code still works as I want! So ROOT somehow distinguishes between empty (zero) and non-empty bins.
Search for “negative” and “empty” in http://root.cern.ch/root/html/THistPainter.html#HP14 and you’ll understand why I prefer to define that funny “{-3.4e38, 1.17e-38, …}” levels (sometimes, it might be convenient to define "{-3.4e38, -1.17e-38, …}, if you want “0” to be drawn with another color).
BTW. Olivier, could you, please, comment on the issue of the “#colors versus #levels” (that I reported in my previous post here) and maybe also on the issue of the “palette bar going to the top of the picture”? Thanks in advance.
Sorry I am doing several other (tricky) things and I lost a bit the track on this one. Can you provide me a small macro showing what I should look at ?
In general, you can directly take the source code given in my post of “Thu May 03, 2012 14:25”: [url]TH2 Drawn with “colz” option - colors and range and then see the “result” of this code which is shown in the next post by “aaduszki” (of “Thu May 03, 2012 23:35”) - you can clearly see the problem of the “palette bar going to the top of the picture” (while we expect is should “end” at the same level as the y-axis).
Then my next post of “Fri May 04, 2012 9:09”: [url]TH2 Drawn with “colz” option - colors and range describes how one can modify this source code in order to see the “#colors versus #levels” problem.
I do not think I have any comments to add… the plot shown here is fine.
Try this:
void palette(Int_t n = 7) {
Int_t *colors = new Int_t[n];
for (Int_t i = 0; i < n; i++) colors[i] = i;
gStyle->SetPalette(n, colors);
// gStyle->SetNumberContours(n);
// #levels <= #colors + 1 (notes: +-3.4e38 = +-FLT_MAX; +1.17e-38 = +FLT_MIN)
Double_t levels[] = {-3.4e38, 1.17e-38, 0.90, 0.95, 1.00, 1.05, 1.10, 3.4e38};
TH2D *h = new TH2D("h", "", 10, 0, 10, 10, 0, 10);
h->SetContour((sizeof(levels)/sizeof(Double_t)), levels);
h->SetStats(kFALSE);
h->SetBinContent(5, 7, 1.20);
h->SetBinContent(5, 6, 1.05);
h->SetBinContent(5, 5, 1.00);
h->SetBinContent(5, 4, 0.95);
h->SetBinContent(5, 3, 0.80);
h->DrawClone("col");// draw "axes", "contents", "statistics box"
h->GetZaxis()->SetRangeUser(0.89, 1.11); // ... set the range ...
h->Draw("z same"); // draw the "color palette"
delete [] colors;
}
Below, see the “palette bar going to the top of the picture”. Moreover, note that all colors in these two pictures are different. I didn’t change the “contour levels”, I just added 3 more colors to the “available” palette (leaving the first 7 colors exactly the same) and this entirely changed the mapping between “contour levels” and “palette colors”. Note also that, in the second picture below, an additional “level” appeared in the “palette” - just above 1.1 it’s green and then above 1.11 it becomes blue (but the top box of the “histogram contents” is green, although it’s 1.20) - that’s not what I asked for when I set my own “contour levels”.
root [] .x palette.cxx(7) 
root [] .x palette.cxx(10) 