Home | News | Documentation | Download

Prediction model using TLinearFitter

Roofit and RooStats
#1

Hi,
lets assume I have a 3- or more-dimensional parameter room and many input-parameters like
f(x0,x1,x2) = value.

I would like to create a polynomial model in order to create a prediction model

I tried to play around with TLinearFitter and created a function of the type:
“1 ++ x[0] ++ x[1] ++ x[2] ++ x[0]*x[0] ++ x[1]*x[1] ++ x[0]*x[1] ++ x[1]*x[2] ++ x[0]*x[2]”

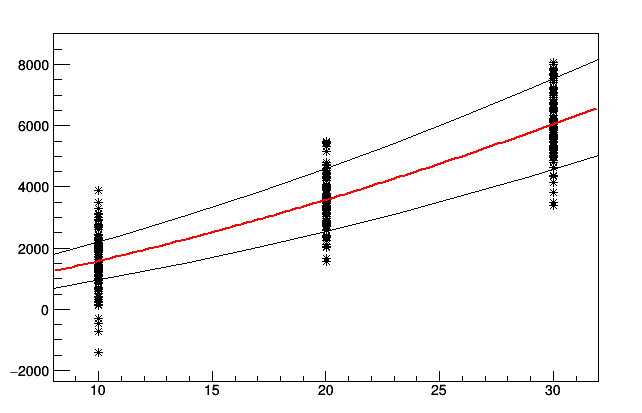
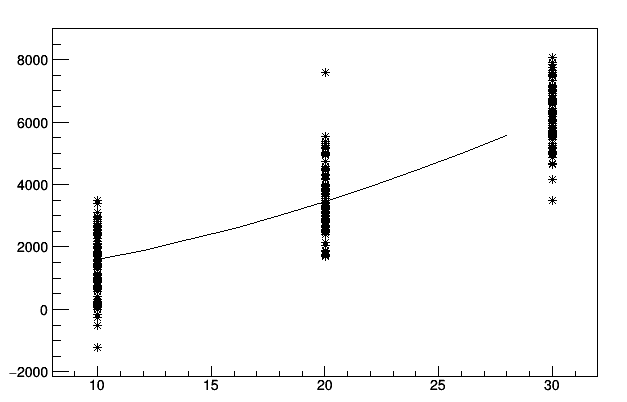
The fit is working I am able to obtain fit parameters and errors.

Now I would like to create a prediction model. In particular I would like to obtain the confidence interval in variation of the position (x0,x1,x2). I create two function:

Double_t GetValue(TLinearFitter *myFit, Double_t par0, Double_t par1, Double_t par2) {
		TVectorD params;
		myFit->GetParameters(params);
		float fitResult = params(0) 
						+ params(1)*par0 
						+ params(2)*par1 
						+ params(3)*par2
						+ params(4)*par0*par0
						+ params(5)*par1*par1
						+ params(6)*par0*par1
						+ params(7)*par1*par2
						+ params(8)*par0*par2;
		return fitResult;
	}
	
	Double_t GetError(TLinearFitter *myFit, Double_t par0, Double_t par1, Double_t par2) {
		TVectorD errors;
		myFit->GetErrors(errors);
		float fitResult = sqrt( 
						std::pow(errors(0),2) 
						+ std::pow((errors(1)*par0),2) 
						+ std::pow((errors(2)*par1),2) 
						+ std::pow((errors(3)*par2),2)
						+ std::pow((errors(4)*par0*par0),2)
						+ std::pow((errors(5)*par1*par1),2)
						+ std::pow((errors(6)*par0*par1),2)
						+ std::pow((errors(7)*par1*par2),2)
						+ std::pow((errors(8)*par0*par2),2)
						);
		return fitResult;
		
	}

The values are correct, but for me it seems that the errors are too large.

Is there another method? Again, I need a confidence inverval(h=0.95) for a point in that prediction model having the meaning: "The confidence interval that the point y at the position x0,x1,x2 is between [a,b] is 95%

Maybe @moneta has an idea?

Georg

#2

Hi again,
I know the question is confusing, so I prepared a little examplefitTest.C (1.4 KB) LFtest.C (7.2 KB)

both files are using the same input-Model or the kind 1 ++ x[0] ++ x[1] ++ x[2] ++ x[0]*x[0] ++ x[1]*x[1] ++ x[0]*x[1] ++ x[1]*x[2] ++ x[0]*x[2]

float inputFormular(float x0, float x1, float x2) {
	float p0 = 0;
	float p1 = 1;
	float p2 = 2;
	float p3 = 3;
	float p4 = 4;
	float p5 = 5;
	float p6 = 6;
	float p7 = 7;
	float p8 = 8;
	
	return p0 +x0*p1 + x1*p2 + x2*p3 + x0*x0*p4 + x1*x1*p5 + x0*x1*p6 + x1*x2*p7 + x0*x2*p8;
	
}
  • a small random gaussian fraction.
    In the file fitTest, the parameters x1 and x2 are fixed to 10 and 1.

In fitTest.C I am generating random-numbers at f(10,10,1) f(20,10,1) and f(30,10,1), I an fitting them with a pol2. Finally I am generating the confidence-intervals via the errors of the individual parameters(using error propagation)fitTest

Working. The two lines representing the upper and the lower confidence interval (sigma = 1, CL = 0,68). One can directly see that only ~68% of the point used for the fit are within the lines, as expected

In the second file LFTest.C I am generating random-numbers at f(10,10,1), f(20,10,1), f(30,10,1), same with f(…,20,1) and f(…,30,1), and f(…,…2).

I’m using the TLinearFitter-Model to create a 3-dim fit with 9 Parameters (Model see above)

As I know the values of the parameters and their corresponding errors I am evaluating the g(x) at f(x,10,1) - this means: fixing two parameters. I am calculating the upper and lower limit in the same way and I am getting
LFTest

The calculation of the values is correct, the calculation of the errors (or the confidence interval) is not. The upper and the lower limit are so close to each other, that cannot be differentiated. I would have expected a similar kind of chart. Please let me know how I can calculate this, of it is a bug (or a feature)

Thanks
Georg

#3

I think @moneta can help.

#4

Hi,
You are not providing the error in each point when using the TLinearFitter. You should add the points passing also the sigma of each point, calling:

myFit->AddPoint(params, val, sigma);

Lorenzo

#5

Hi,
…but I’m not doing this is case of TGraph either?? (Actually all input values are individual values, no distributions)

I was able to simplify the example above:
Lets take the fitTest.C, which is a simple pol2 Fit - working!
Now, here is a new LFtest2.C (2.9 KB)
which is a simple implementation of a pol2 fit with TLinear Fitter (see the first line here)

TLinearFitter *myFit = new TLinearFitter(1);
myFit->SetFormula(“1 ++ x[0] ++ x[0]*x[0]”);

Running the TGraph-Fit (working) will produce an uncertainty of

Error at 20 is 1030.46

The same uncertainty using TLinear Fitter gives:

Calculating Point at (10,10,1):106.023 ± 0.67082

For me it seems that there is a bug in the error-calculation of the TLinearFitter. The calculated uncertainty needs to be (almost) the sigma in the input (which is 1000 in the examples)

Thanks for your help in advance

Georg

#6

Hi,
The error of the TGraph::Fit is rescaled with the factor sqrt(chi2/ndf), If you do not add a weight (error) for each point, then you should do that to get a reasonable error on the parameters.

Lorenzo

#7

Hi Lorenzo,
thanks for your reply.

That means that I have two possibilities: Either back-scaling or entering of an error, right?
Approach 1:
Entering an error.
Please help me, I think I’m misunderstanding you completely. What kind of error or weight should I use here. All entered values have equal weight and are direct measurements without underlying distribution.
(E.g. if 100 people are counting the number of pebbles in a box, what is the error of the counting results?)

Approach 2:
I tried to back-scale the errors of the TLinear Fitter. I am replacing

error(i)

by

Double_t chi2 = myFit->GetChisquare();
Double_t ndf = myFit->GetNumberFreeParameters();
error(i)*sqrt(chi2/ndf)

When I’m comparing the fit-results of the TGraph

Minimizer is Linear / Migrad
Chi2 = 2.69546e+08
NDf = 297
p0 = -538.466 +/- 415.255
p1 = 60.7083 +/- 47.1543
p2 = 0.374068 +/- 1.16677

with the results of TLinearFitter (incl. the sqrt(ch2/ndf)-correction:

par[0]: -538.466 ± 4131.73
par[1]: 60.7083 ± 469.179
par[2]: 0.374068 ± 11.6092

the errors appear to be a factor of 10 wrong. Why? (I checked the results seem to be stable independent from the number of entries)

Thanks Georg

#8

found out by myself:

NDF is not

Double_t ndf = myFit->GetNumberFreeParameters();

NDF is

Double_t ndf = myFit->GetNpoints()-myFit->GetNumberFreeParameters();

I would recommend to put the differences of the errors of TLinearFitter and TGraph/TGraphErrors in the Docs. It’s really not self explaining

Georg

#9

Hi,

If you know the error you should use. In your example you were smearing the points with a Gaussian and a given sigma. So you should use that sigma as the weight.

Then , yes NDF = number of fit points - number of free parameters !

I agree, we should document better the scaling of the errors in Graph and mention also in TLinearFitter/TGraphErrors fitting. It would be great if you could open a GitHub issue on this so we will not forget it

Best regards

Lorenzo