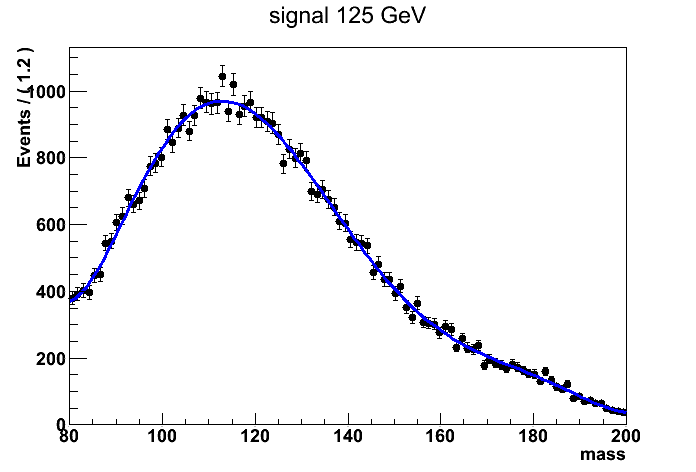
Dear Experts
I want to fit psudo data (80-200) with polynomial function in sub-ranges 80-100 and 140-200 simultaneously.
I try to follow given tutorials and various discussion in forum but not able to get correct fit in subrange.
Have a look on the attched macro which run out of the box. How I can fit sub-range and then extrapolate it in the non-fitted region.
Thanks for your help!
Regards-Sunil
toyMC_study_v2.C (1.98 KB)
Hi Sunil,
For the Chebychev polynomials this is difficult, because in the interpretation of the coefficients is done in the normalization range of the observables, i.e. if you change the range (or plan to work with multiple ranges) the shape of the pdf will change.
To work around this you can either use the regular polynomials (RooPolyniomial) which have an ‘absolute’ interpretation of the range, your have to defined a custom copy of RooChebychev that implements the definition of the pdf in terms of a fixed reference range. Otherwise you can consider to use a non-polynomial pdf shape (in fact RooChebyshev is the only pdf that has this feature)
Wouter
Thanks Wouter
I checked range function with Voigtian function and it working perfectly fine. I will try to use RooPolynomial but
I used to face problem in convergence while using this.
Regards-Sunil
Hi Wouter
I think that RooPolynomial is good option to fit the shape which we have as attached. I was looking at
post
Fitting polynomial using roofit
Where you mentioned that RooPolynomial is not good for shape is which vanish at x=0. I think it is applicable to our data shape as well. What do you think? This mean I can’t use RooPolynomial as well as RooChebchev for one or another reason  . Is it correct??
. Is it correct??
Thanks for your feedback!
Regards-Sunil
Hi Sunil,
The standard formulation of RooPolynomial is 1 + a0x + a1x*x etc…
so that’s not great of it needs to be zero at x=0. You can however reconfigure
RooPolynomial in the ctor to interpret a0 as the offset and set it to zero to avoid
this. However in that case you should fix at least one of the other coefficients
to a fixed value to avoid convergence problems: a normalized N-term polynomial
has only N-1 degrees of freedom (as one is taken by the normalization)
Wouter
sorry to bother you again wouter
I did not understood how you suggesting to change RooPolynomial. <img src="/uploads/default/original/1X/378b417f7f25e635458e14f511257ba15acc7a37.gif" width="22" height="16" alt="#-o" title="d'oh!"/>
You mean to change last argument of constructor?
RooPolynomial(const char* name, const char* title, RooAbsReal& _x, const RooArgList& _coefList, Int_t lowestOrder = 1)
Can you please clarify it a bit more?
Thanks
Regards-Sunil
 . Is it correct??
. Is it correct??