Plotting the variables of a 2D model

[Antonio83]

Dear all,

I am trying to extend the 1D model I posted here:

RooFit: include shape systematics

Dear all, I am trying to create a model like this (f*signal + (1-f)*background). Other than the parameter of interest, the signal fraction, I need to include also a nuisance parameter, accounting for the systematics on the background shape. The background shape variation is defined by a nominal distribution, and the two distributions corresponding to ±1 sigma variations, respectivelly. So I am using the PiecewiaeInterpolation class to model the shape systematic through a parameter alpha. From…

to a 2D model.

The model is built from TH2F histograms with different number of bins for the two variables. I have a weird behabiour when plotting the distributions of the variables: the model does not match with both the initial parameter values before fitting and with the fitted parameters after performing the fit:

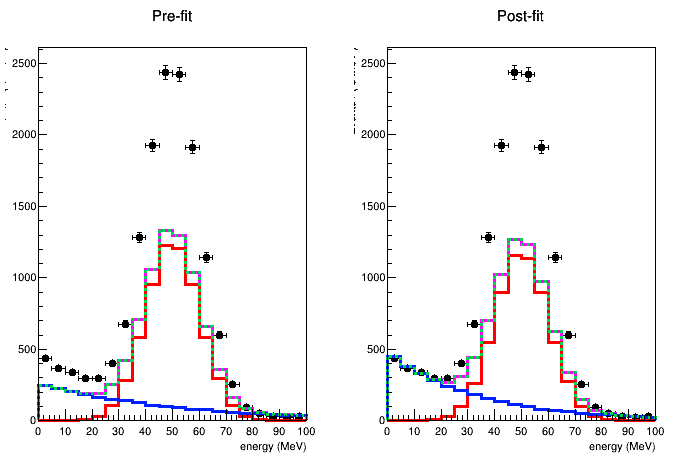
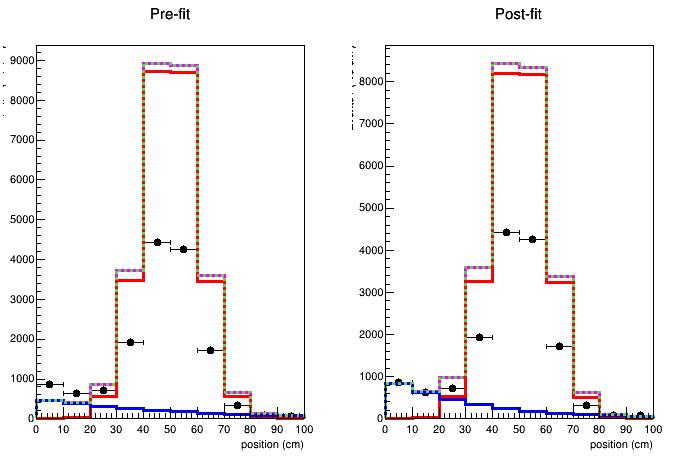
It seems just a problem related to the plots, because the fit is able to find the actual vaues of the parameters.

The behaviour is the expected one if the number of bins is the same for both variables.

Here is the macro:

void test_morph()
{
	// signal 
	TH2F* hsgn = new TH2F("hsgn","nominal bkg", 20, 0, 100, 10, 0, 100);
	TF2* g = new TF2("g","[0]*exp(-(x-[1])^2/(2*[2]^2))*exp(-(y-[1])^2/(2*[2]^2))", 0, 100, 0, 100);
	g -> SetParameters(100, 50, 10);
	hsgn -> FillRandom("g", 100000);

	// background
	TH2F* hbkg_nom = new TH2F("hbkg_nom","nominal bkg", 20, 0, 100, 10, 0, 100);
	TF2* fe = new TF2("fe","[0]*exp(-[1]*(x+y))", 0, 100, 0, 100);
	fe -> SetParameters(50, 0.02);
	hbkg_nom -> FillRandom("fe", 80000);

	TH2F* hbkg_p = new TH2F("hbkg_p","+1 sigma bkg", 20, 0, 100, 10, 0, 100);
	fe -> SetParameters(55, 0.03);
	hbkg_p -> FillRandom("fe", 150000);

	TH2F* hbkg_m = new TH2F("hbkg_m","-1 sigma bkg", 20, 0, 100, 10, 0, 100);
	fe -> SetParameters(45, 0.01);
	hbkg_m -> FillRandom("fe", 50000);

	// define observables
	RooRealVar e{"e", "energy", 0, 100, "MeV"};
	RooRealVar x{"x", "position", 0, 100, "cm"};
	e.setBins(Int_t(20));
	x.setBins(Int_t(10));
	
	// signal pdf
	hsgn -> Scale(1./hsgn -> Integral());
	RooDataHist dh_sgn{"dh_sgn", "dh_sgn", RooArgSet{e,x}, hsgn};
	RooHistFunc sgn("sgn", "sgn", RooArgSet{e,x}, dh_sgn);

	// background pdf
	//
	// nominal value
	hbkg_nom -> Scale(1./hbkg_nom -> Integral());
	RooDataHist dh_bkg_nom{"dh_bkg_nom", "dh_bkg_nom", RooArgSet{e,x}, hbkg_nom};
	RooHistFunc bkg_0("bkg_0", "bkg_0", RooArgSet{e,x}, dh_bkg_nom);
	//
	// bkg +1 sigma
	hbkg_p -> Scale(1./hbkg_p -> Integral());
	RooDataHist dh_bkg_p{"dh_bkg_p", "dh_bkg_p", RooArgSet{e,x}, hbkg_p};
	RooHistFunc bkg_p("bkg_p", "bkg_p", RooArgSet{e,x}, dh_bkg_p);
	//
	// bkg -1 sigma
	hbkg_m -> Scale(1./hbkg_m -> Integral());
	RooDataHist dh_bkg_m{"dh_bkg_m", "dh_bkg_m", RooArgSet{e,x}, hbkg_m};
	RooHistFunc bkg_m("bkg_m", "bkg_m", RooArgSet{e,x}, dh_bkg_m);
	//
	// build interpolation between -1 -> +1 sigma
	RooRealVar alpha{"alpha", "alpha bkg sys", 0, -5, 5};
	PiecewiseInterpolation bkg_sys("bkg_sys", "bkg_sys", bkg_0, bkg_m, bkg_p, alpha);

	// build model
	double f_val = 0.8;
	RooRealVar f{"f", "f", f_val, 0, 1};
	// Can not use RooAddPdf: check https://root-forum.cern.ch/t/roofit-include-shape-systematics/41382
	//RooAddPdf model{"model", "model", RooArgSet{sgn, bkg_sys}, f};
	RooRealSumPdf sb{"sb", "sb", RooArgSet{sgn, bkg_sys}, f};

	// introduce alpha constraint
	RooGaussian gaus_alpha("gaus_alpha", "gaus_alpha", alpha, RooFit::RooConst(0), RooFit::RooConst(1));
	RooProdPdf model{"model", "model", sb, gaus_alpha};
	
	alpha.setVal(1);
	RooDataHist* data = model.generateBinned(RooArgSet{e,x}, 15000, RooFit::Verbose(1));

	// initial values for par
	f.setVal(f_val+0.05);
	alpha.setVal(0.0);
	//alpha.setConstant(kTRUE);

  // e variable
	auto eframe = e.frame(RooFit::Title("Pre-fit"));

	data->plotOn(eframe);

	model.plotOn(eframe, RooFit::LineColor(6));
	model.plotOn(eframe, RooFit::LineColor(2), RooFit::Components("sgn"));
	model.plotOn(eframe, RooFit::LineColor(4), RooFit::Components("bkg_sys"));
	model.plotOn(eframe, RooFit::LineColor(8), RooFit::LineStyle(kDashed), RooFit::Components("bkg_sys,sgn"));

  // x variable
	auto xframe = x.frame(RooFit::Title("Pre-fit"));

	data->plotOn(xframe);

	model.plotOn(xframe, RooFit::LineColor(6));
	model.plotOn(xframe, RooFit::LineColor(2), RooFit::Components("sgn"));
	model.plotOn(xframe, RooFit::LineColor(4), RooFit::Components("bkg_sys"));
	model.plotOn(xframe, RooFit::LineColor(8), RooFit::LineStyle(kDashed), RooFit::Components("bkg_sys,sgn"));

	// fit
	auto fitres = model.fitTo(*data, RooFit::Constrain(alpha), RooFit::Save());

	fitres->Print();

  // e variable
	auto eframe1 = e.frame(RooFit::Title("Post-fit"));

	data->plotOn(eframe1);

	model.plotOn(eframe1, RooFit::LineColor(6));
	model.plotOn(eframe1, RooFit::LineColor(2), RooFit::Components("sgn"));
	model.plotOn(eframe1, RooFit::Components("bkg_sys"), RooFit::LineColor(4));
	model.plotOn(eframe1, RooFit::LineColor(8), RooFit::LineStyle(kDashed), RooFit::Components("bkg_sys,sgn"));

  // x variable
	auto xframe1 = x.frame(RooFit::Title("Post-fit"));

	data->plotOn(xframe1);

	model.plotOn(xframe1, RooFit::LineColor(6));
	model.plotOn(xframe1, RooFit::LineColor(2), RooFit::Components("sgn"));
	model.plotOn(xframe1, RooFit::LineColor(4), RooFit::Components("bkg_sys"));
	model.plotOn(xframe1, RooFit::LineColor(8), RooFit::LineStyle(kDashed), RooFit::Components("bkg_sys,sgn"));

	TCanvas* c = new TCanvas();
	c->Divide(2,1);

	c->cd(1);
	eframe -> Draw();

	c->cd(2);
	eframe1 -> Draw();

	TCanvas* c1 = new TCanvas();
	c1->Divide(2,1);

	c1->cd(1);
	xframe -> Draw();

	c1->cd(2);
	xframe1 -> Draw();

}

Should I use some settings that I am missing?

Thanks for your help.

[jblomer]

@StephanH Can you help?

[StephanH]

Hi @Antonio83,

I’m on it, but I don’t have an answer yet.

[Antonio83]

Hi @StephanH,

thanks for looking into this.

Just as a remark: I noticed that if using RooHistPdf instead of RooHistFunc the bahaviour is as I would expect.

[StephanH]

Oh, but that’s probably the answer:
A HistFunc is just a function, so it doesn’t get normalised to the correct number of events when you plot.
A HistPdf is by definition normalised to unity, but when you plot it together with data, RooFit automatically scales it up to match the number of data events.
Makes sense?

[Antonio83]

ok, I have to think about it

I was expecting a pdf behaviour since the HistFunc are built from normalized histos: so I was thinking that in the final model each component should be normalized to one, and the total pdf:

PDF = Sum_i f_i * PDF_i + (1 - Sum_i f_i ) * PDF_n

In this case, the denominator in the general form reported here:

https://root.cern/doc/master/classRooRealSumPdf.html

is one and each component contributes with its fraction f (set to initialization before fit or to fitted values after fit) to the total pdf. When generating a set of data then each component should have a weight given by f.

It actually seems that the pdf is correctly producing the data, but when projecting the model is lower on x and higher on y. So, when you say that the HistFunc doesn’t get normalized to the data in the plots, you mean that the “issue” is only related to the visualization? I am a bit confused.

Anyway, I was using HistFunc instead of HistPdf because of negative values problems, but since it seems that I can overcome this problem, using HistPdfs should solve everything.

[StephanH]

Indeed, if the HistFuncs are summed by a RooRealSumPdf, the PDF should be normalised properly. It’s really hard to track down if it’s “only” a visualisation problem, so I would advise to use the HistPdfs.

[Antonio83]

Hi @StephanH,

ok, thanks for your help. I’ll use the HistPdf.