Hello Roofit experts,
I wanted to fit a function in the form of an integral with variable limits to a data set. Fo this, I made a code which first does the integration. The integration works if Tmb and Tbe are constants . But I need to make them as a paramenter for the fit. Can you please tell me as to how I do that with the present form of my RooGenericPdf fmb and fbe ?
#ifndef __CINT__
#include "RooGlobalFunc.h"
#endif
#include "RooRealVar.h"
#include "RooGenericPdf.h"
#include "RooDataSet.h"
#include "RooProdPdf.h"
#include "RooGaussian.h"
#include "RooConstVar.h"
#include "RooExponential.h"
#include "TCanvas.h"
#include "TAxis.h"
#include "RooPlot.h"
#include "RooFitResult.h"
#include "RooDataHist.h"
#include "RooDataSet.h"
#include "TH1F.h"
#include "TFile.h"
#include "TH1F.h"
#include "TList.h"
#include "TLegend.h"
#include "TStyle.h"
#include "TLine.h"
#include "TCanvas.h"
#include <cmath>
using namespace RooFit ;
void testIntegration()
{
//setup variables
RooRealVar p("p","p",0.0,0.0,22.4);
RooRealVar c("c","c",0.0,0.0,1.0);
RooConstVar mass("mass","mass",0.139);
RooConstVar Tmb("Tmb","Tmb",0.086);
RooConstVar Tbe("Tbe","Tbe",0.091);
//RooRealVar Tmb("Tmb","Tmb",0.0,0.6);// Needs to to Give as Paramenter for the fit
//RooRealVar Tbe("Tbe","Tbe",0.0,0.6);// Needs to to Give as Paramenter for the fit
//Create pdf
RooGenericPdf fmb("fmbA","fmbA","pow(p,2)*(exp(-sqrt((pow(p,2) + pow(mass,2)))/Tmb)) ",RooArgList(p,mass,Tmb));
RooGenericPdf fbe("fbeA","fbeA","pow(p,2)/(exp(sqrt((pow(p,2) + pow(mass,2)))/Tbe) - 1)",RooArgList(p,mass,Tbe));
//Create Limit Function
RooFormulaVar max("max","max","((-TMath::Log(2.0)*22.4*c) + sqrt( pow((TMath::Log(2.0)*22.4),2) - (pow(mass,2)*(1-pow(c,2))))) /(1-pow(c,2))",RooArgList(c,mass));
RooRealVar min("min","min",0.);
//Set Range For integration
p.setRange("range",min,max);
//Do the integration
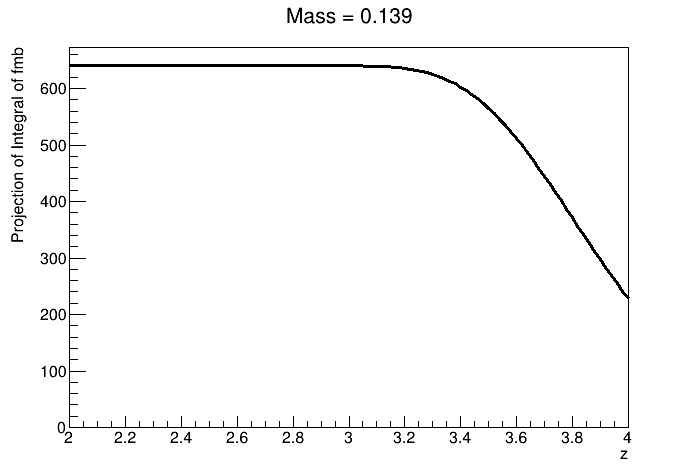
RooAbsReal* pdfMB = fmb.createIntegral(p,p,"range");
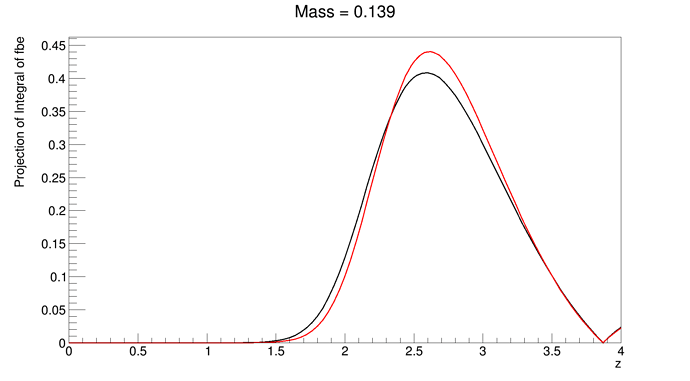
RooAbsReal* pdfBE = fbe.createIntegral(p,p,"range");
//Create a frame
RooPlot* frame = c.frame(Name("frame"),Title("Result of Integration Integration"));
TFile* File1 = TFile::Open("/home/rahul/Documents/result.root");
if(!File1) printf("File1 Not Found");
TList* list1 = dynamic_cast<TList*> (File1->Get("HistList"));
if(!list1) printf("List1 Not Found");
TH1F* fHist1 = (TH1F*)list1->FindObject("fCG[%d]");
if(!fHist1) printf("Hist Not Found");
TH1F* fHist2 = (TH1F*)list1->FindObject("fCL[%d]");
if(!fHist2) printf("Hist2Not Found");
RooDataHist dhG("dhG","dhG",c, fHist1) ;
RooDataHist dhL("dhL","dhL",c, fHist2) ;
pdfBE->plotOn(frameMB,LineColor(kRed));
pdfMB->plotOn(frameMB,LineColor(kBlack));
// pdfMB->fitTo(dhG);// chi2FitTo() ??
TCanvas* MB = new TCanvas("CMB","CMB");
frameMB->Draw();
}
I pasted the code above.
Regards
Rahul