Difference between RooRealSumPdf and RooAddPdf

[aaronsw]

Hi, I’m trying to use an extended RooRealSumPdf, but I get a discrepancy from an extended RooAddPdf. The model is uniform+gaussian. The implementations are:

    modelRSP = RooRealSumPdf("modelRSP","modelRSP",
                      RooArgList(w.pdf("bkg"),    w.pdf("sig")),
                      RooArgList(w.var("bkgNorm"),w.var("sigNorm")),
                      True
                     )

And

    modelRAP = RooAddPdf("modelRAP","modelRAP",
                      RooArgList(w.pdf("bkg"),    w.pdf("sig")),
                      RooArgList(w.var("bkgNorm"),w.var("sigNorm")),
                     )

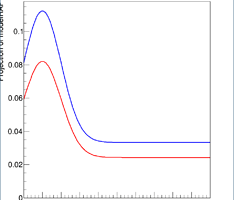
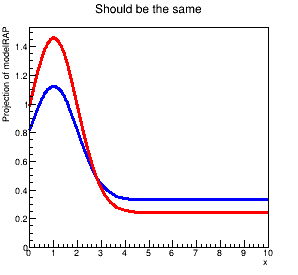
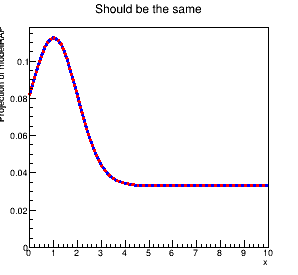
When I plot these, I get two different results. In particular, even with the same sigNorm value, the RooRealSumPdf seems to have less signal than the RooAddPdf. The plot shows the discrepancy:

I have a stand-alone example of this: errorDemoAddPdfVsSumPdf.py (4.3 KB). Am I missing something here? I’ve tried extending the uniform and gaussian components manually, but I get a similar result. Any help would be very appreciated.

[StephanH]

Hello @aaronsw,

one difference between the two is that only the AddPdf reacts to

modelRAP.fixAddCoefNormalization(RooArgSet(x),True)
modelRAP.fixAddCoefRange("fit",True)

for a RealSumPdf, these calls won’t change anything.

I removed the manual extension, and also the fixing of coefficients and ranges. That reveals normalisation differences:

>>> modelRSP.getNorm(RooArgSet(x))
[#1] INFO:NumericIntegration -- RooRealIntegral::init(bkg_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
11.054469264603824
>>> modelRAP.getNorm(RooArgSet(x))
1.0

That’s likely because the RooAddPdf is a sum of PDFs, whereas the RooRealSumPdf is a sum of functions. For the former, the PDFs are first normalised, then added. For the latter, the (unnormalised) PDFs are added, and then normalised. That means that their relative fractions change.

To demonstrate that, I explicitly normalised the uniform distribution by putting 1./10. instead of 1., and got the following result:

So I tried to match the AddPdf distribution exactly, by explicitly normalising the functions (they are not PDFs, as far as the RooRealSumPdf is concerned) before the summation:

    integralSig = sig.getNorm(RooArgSet(x))
    integralBkg = bkg.getNorm(RooArgSet(x))
    print("Unnormalised PDFs yield:", integralSig, integralBkg)
    
    normaliserSig = RooConstVar("normaliserSig", "normaliserSig", 1./integralSig)
    normaliserBkg = RooConstVar("normaliserBkg", "normaliserBkg", 1./integralBkg)
    sigNormScaled = RooProduct("scaledSigNorm", "bkgNorm/Int[bkg]",
        RooArgList(sigNorm, normaliserSig))
    bkgNormScaled = RooProduct("scaledBkgNorm", "bkgNorm/Int[bkg]",
        RooArgList(bkgNorm, normaliserBkg))
    
    modelRSP = RooRealSumPdf("modelRSP","modelRSP",
                      RooArgList(w.pdf("bkg"),    w.pdf("sig")),
                      RooArgList(bkgNormScaled,sigNormScaled),
                      True
                     )

Result:

Unnormalised PDFs yield: 2.1089385292076486 10.0

and (using modelRSP.plotOn(frame,RooFit.LineColor(kRed),RooFit.LineStyle(kDashed))):

If you normalise explicitly, the coefficients sigNorm and bkgNorm can be interpreted in the same way both with the Add and the RealSumPdf.

[aaronsw]

Hi @StephanH,

This explains a lot. I had hoped the manual extension to force a normalization, but using RooProduct looks like it works. Thanks very much for the help and the explanation!