Hi @moneta,
I’ve also been digging into the WL fit, and I was wondering how ROOT actually calculates the weighted negative log-likelihood (NLL) to be minimized.
According to the code you shared, the NLL is computed through lines 1567-1586 with the WL option.
The only difference between the standard L fit is that you multiply weight = (error * error) / y; (Line 1577) to the NLL for each bin (leaving aside when the bin content (y) is 0 for the moment).
So I ran a quick test to compare the NLL for the L fit and NL fit.
Here are my codes:
int nbins = 10;
double c_true = 4.5;
TH1F* h = new TH1F("h", "", nbins, 0, nbins);
TF1* f = new TF1("f", "[0]", 0, nbins);
TRandom3* rng = new TRandom3(seed);
for (int i=0; i<nbins; i++) {
for (int j=0; j<rng->Poisson(c_true); j++) {
h->Fill(i, rng->Rndm());
}
}
TFitResultPtr r1 = h->Fit("f", "QSR0"); // Chi-square fit
TFitResultPtr r2 = h->Fit("f", "QSRL0"); // Likelihood fit
TFitResultPtr r3 = h->Fit("f", "QSRWL0"); // Weighted likelihood fit
TGraph* g1 = new TGraph();
TGraph* g2 = new TGraph();
TGraph* g3 = new TGraph();
double theta_start = 0.1;
double theta_end = 3;
f->FixParameter(0, 0);
for (double theta=theta_start; theta<theta_end; theta+=0.01)
{
f->SetParameter(0, theta);
double nll = 0;
for (int i=0; i<nbins; i++) {
double y_i = h->GetBinContent(i+1);
double e_i = h->GetBinError(i+1);
double sum_of_weights = y_i;
double sum_of_weight_squared = e_i * e_i;
double scale_factor = sum_of_weight_squared / sum_of_weights;
nll += scale_factor * (y_i * (log(y_i) - log(theta)) + theta - y_i); // Weighted likelihood fit.
}
TFitResultPtr r1_ = h->Fit("f", "QSRL0");
g1->SetPoint(g1->GetN(), theta, r1_->MinFcnValue());
TFitResultPtr r2_ = h->Fit("f", "QSRWL0");
g2->SetPoint(g2->GetN(), theta, r2_->MinFcnValue());
g3->SetPoint(g3->GetN(), theta, nll);
}
std::cout << "\nChi-squared fit" << std::endl;
std::cout << "Fit\t" << r1->Parameter(0) << "\t" << r1->ParError(0) << std::endl;
std::cout << "\nLikelihood fit" << std::endl;
std::cout << "Fit\t" << r2->Parameter(0) << "\t" << r2->ParError(0) << std::endl;
std::cout << "\nWeighted likelihood fit" << std::endl;
std::cout << "Fit\t" << r3->Parameter(0) << "\t" << r3->ParError(0) << std::endl;
TCanvas* c = new TCanvas("c", "", 800, 600);
g1->SetLineColor(kBlue);
g1->SetLineWidth(2);
g1->Draw("apl");
g2->SetLineColor(kRed);
g2->Draw("same");
g3->SetLineColor(kGreen);
g3->Draw("same");
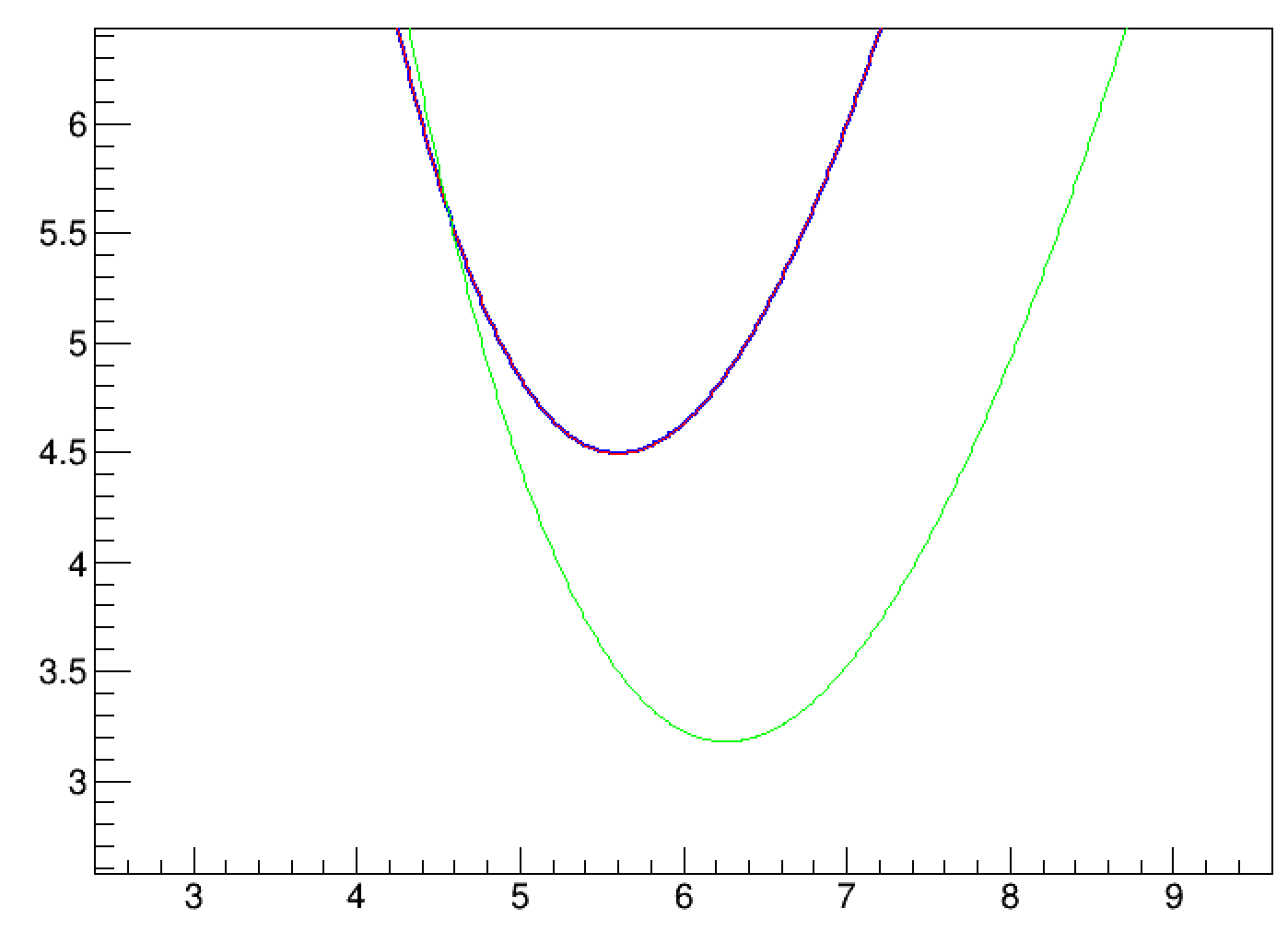
I made a simple histogram with weighted Poisson variables and fitted it with a constant (theta).
g1 is the NLL vs. theta in the likelihood fit (blue),
g2 is the NLL vs. theta in the weighted likelihood fit (red), and
g3 is the NLL vs. theta from the same formula used in ROOT for the WL fit (green).
I expected that red and green are the same, and they are different from blue.
However, the resulting plot shows that red is the same as blue.
It suggests that your NLL for the WL fit is exactly the same as that for the L fit, in contrast to what’s implemented in lines 1567-1586 of your code, which confused me.
And it is unclear to me how the WL fit calculates the covariance matrix.
This could be a separate question, but I also have a doubt about the NLL for the weighted Poisson case.
I followed the references you put and derived that the scale factor should be divided, not multiplied, in the likelihood.
So I believe the line 1577 should be weight = y / (error * error); instead of weight = (error * error) / y;
To sum up, I have 3 questions:
- The NLL in the
WL fit seems to be exactly the same as that in the L fit, as opposed to what’s written in the source code. There might be a bug.
- Still, the variance of parameters from the
WL fit is different from the L fit. How the covariance matrix is computed in the WL case?
- The weight
weight = (error * error) / y; seems to be corrected to weight = y / (error * error);
Best regards,
On