Hello Stephan,
This is off topic to what I was discussing with you last week, but I figured this would be the best place to ask some follow up questions.
I suspect I am not fully understanding how RooFit handles event generation with some pre-defined PDF. I have the following code:
#include <RooFit.h>
#include <RooRealVar.h>
#include <RooAbsReal.h>
#include <RooDataSet.h>
#include <RooRandom.h>
#include <RooFormulaVar.h>
#include <RooMinuit.h>
#include <TF1.h>
#include <TGraph.h>
#include <TFile.h>
#include <TTree.h>
using namespace RooFit;
TGraph* g;
TGraph* g2;
double theFunction(Double_t* x, Double_t*){
double num = g->Eval(x[0]);
return num;
}
void likelihoodInterpreter(){
RooRandom::randomGenerator()->SetSeed(62);
std::cout << "Loading our data!" << std::endl;
TFile* file = new TFile("t0-analyzed.root", "OPEN");
TTree* tree = (TTree*)file->Get("mean");
g = (TGraph*)file->Get("mean-time");
TFile* file2 = new TFile("OUTPUT-SimData-Neutron-Batch-0.root");
TTree* tree2 = (TTree*)file2->Get("temp");
RooRealVar tim("time", "time", -0.02, 10);
RooRealVar cts("counts", "counts", 0, 100);
RooDataSet SimData("SimData", "SimData", RooArgSet(tim), Import(*tree2));
std::cout << "Creating our variables and formulas!" << std::endl;
RooRealVar t("t", "t", -0.02, 10);
RooRealVar mean("mean", "mean", 0, 26);
RooRealVar t0("t0", "t0", 0);
RooFormulaVar tPrime("tPrime", "t-t0", RooArgList(t,t0));
std::cout << "Creating our function and poisson PDF!" << std::endl;
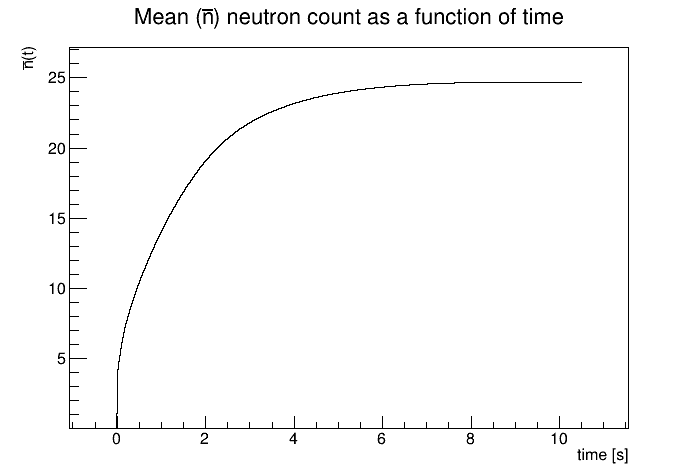
// This repersents the mean as a function of the monte carlo truth time.
TF1* f = new TF1("f", theFunction, -0.02, 10);
TCanvas* c = new TCanvas("c", "c", 400, 400);
c->Divide(3,1);
// We bind this to our time.
RooAbsReal* f1 = RooFit::bindFunction(f, t);
RooPoisson poisson("poisson", "poisson", t, *f1, kFALSE);
int points = 246891;
std::cout << "Generate our data!" << std::endl;
TFile* output = new TFile("output-test.root", "RECREATE");
RooDataSet* data = poisson.generate(t, points);
// Get the Geant4 Monte Carlo data.
TFile* tempFile = new TFile("createCountPDF.root", "OPEN");
TTree* tempTree = (TTree*)tempFile->Get("data");
RooRealVar timeDist("timeDist", "timeDist", -0.02, 10);
RooDataSet MC("MC", "MC", RooArgSet(timeDist), Import(*tempTree));
c->cd(3);
RooPlot* frame3 = timeDist.frame();
MC.plotOn(frame3, Binning(10020));
frame3->Draw();
c->cd(2);
RooPlot* frame = t.frame();
data->plotOn(frame, Binning(10020));
frame->Draw();
c->cd(1);
RooPlot* frame2 = t.frame();
f1->plotOn(frame2);
frame2->Draw();
data->Write();
}
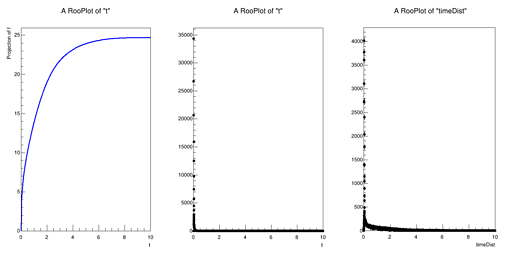
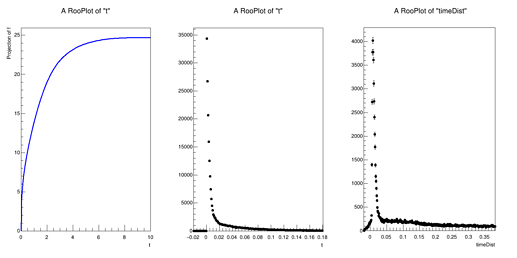
I was working with the bindFunction() function you suggested last week to load a TF1 object of my mean (as a function of time) and then hand that over to my RooPoisson. I generate a few hundred thousand points from this Poisson distribution and get a toy data set that is wildly inconsistent with a dataset that comes directly from the Geant4 Monte Carlo. In the attached figure(s), the middle is the toy dataset and the right is the Monte Carlo. It almost appears like the toy data is a simple exponential, there is also some features in the Geant4 data set that are not accurately reflected in the toy data set. The left plot is the RooAbsReal f1, which is the mean (as a function of time) and is fine. Does anything jump out to you in my code in how I am defining my distribution? Is anything blatantly incorrect? I apologize if this is trivial and for my frequent questions.
To run the above code, there is two ROOT files you will need that were not present in our previous discussions. See below.
createCountPDF.root (1.8 MB)
t0-analyzed.root (14.8 KB)
 .
.