TH2F polar Histogram with bins of equal size

ROOT
1

Dear Rooters,

I’m currently trying to plot a polar histogram, in which every bin has the same area. For example at r=0 there would only be 1 bin for phi (basically a circle), while on higher r the annulus would be divided into several bins with the same area as the circle at r=0. I tried to achieve this with the variable bin size option of the TH2F class, but since this still gives you the same number of bins for every radius, it didn’t work.

(so something similar to this: [url]TH2Poly in polar coordinates unfortunately there was no solution for this binning problem provided there.)

Is there any option to achieve this binning? I guess one could do it by plotting the histogram in several steps, where each step plots a range of radius, which corresponds to the radius binning i’m using right now, but im hoping for a more elegant solution.

Regards

2

I do not think there is a easy solution to your question.
May be you can post here what you already achieved …?

3

I think, that I got a working solution now. I basically rebinned the histogram for each r independently.
Here is the Code:

[code]#include <TH1.h>
#include <TH2.h>
#include <TCanvas.h>
#include <TFile.h>
#include <TRandom3.h>
#include
#include <math.h>
using namespace std;

void polar_gauss() {
TRandom3 rnd;
Int_t nbinphi = 20, nbintheta = 10;
Double_t phimin = 0, phimax = 360, thetamin = 0, thetamax = 90;
TH2F *histo2d = new TH2F(“h2d”,“2DHistogramm”, nbinphi, phimin, phimax, nbintheta, thetamin, thetamax);
TH2F *new_histo2d = new TH2F(“h2d”,“2DHistogramm”, nbinphi, phimin, phimax, nbintheta, thetamin, thetamax);

Double_t dphi = (phimax-phimin)/(nbinphi-1), dtheta = (thetamax - thetamin) / (nbintheta-1);

//I left out the filling of histo2d with phi and theta

//////////////////////////////////////////////////////////
// rebinning //
//////////////////////////////////////////////////////////

Double_t bincontent[100][100];
for (Int_t Ny = 1; Ny < nbintheta + 1; Ny++)
{
Int_t i = 0;
Double_t actual_theta = (Ny - 1.) * dtheta;
//number of new bins for current theta (area of annulus divided by area of circle at theta=0)
Double_t N = (pow(actual_theta+dtheta,2) - pow(actual_theta,2))/pow(dtheta,2);

for(Int_t Nx = 1; Nx < nbinphi + 1; Nx++)
{
	if (Nx > (i + 1) * (nbinphi / N)) //if the bin gets split in the new binning
	{
		for (Int_t a = 0; a < histo2d->GetBinContent(Nx, Ny); a++) //throw dice for every entry to determine, in which new bin it gets stored
		{
			if (rnd.Rndm(a) >= (i + 1) * (nbinphi/N) - (Int_t)((i + 1) * nbinphi/N)) bincontent[Ny-1][i+1]++;
			else bincontent[Ny-1][i]++;			
		}
		cerr << bincontent[Ny-1][i] << "\t" << bincontent[Ny-1][i+1] << "\t";
		//cerr<< "vergleich:" << (i + 1) * N - (Int_t)((i + 1) * N) << "\t" << bincontent[Ny-1][i+1] << "\t";
		i++; //go to next new bin
	}
	else {bincontent[Ny-1][i] += histo2d->GetBinContent(Nx, Ny); cerr << bincontent[Ny-1][i] << "\t" << bincontent[Ny-1][i+1] << "\t";}
}

}

//store new binning in a new histogram
for (Int_t Ny = 1; Ny < nbintheta + 1; Ny++)
{
Int_t i = 0;
for(Int_t Nx = 1; Nx < nbinphi + 1; Nx++)
{
Double_t actual_phi = (Nx -1.)*dphi;
if (actual_phi == 360) actual_phi = 360-0.01; //it doesn’t like phi=360°
Double_t actual_theta = (Ny - 1.)*dtheta;
Double_t N = (pow(actual_theta+dtheta,2) - pow(actual_theta,2))/pow(dtheta,2);
new_histo2d->Fill(actual_phi, actual_theta, bincontent[Ny-1][i]);
if (Nx > (i + 1) * (nbinphi / N)) i++; //increment i after end of new bin is reached
}
}

////////////////////////////
// graphical representation
////////////////////////////
//dummy for axis
TH2D* dummy_his = new TH2D(“dummy”, “histo title”, 100, -thetamax, thetamax, 100, -thetamax, thetamax);

TCanvas* c1 = new TCanvas(“c1”,“gauss”,0,10,1800,1000);
c1->Divide(2,2);

c1->cd(1);
dummy_his->Draw(“COL”); // draw the dummy histogram first
histo2d->Draw(“COLZ POL SAME”);
c1->cd(2);
dummy_his->Draw(“COL”);
new_histo2d->Draw(“COLZ POL SAME”);
c1->cd(3);
dummy_his->Draw(“COL”);
new_histo2d->Draw(“SURF2 pol”);
c1->cd(4);
dummy_his->Draw(“COL”);
new_histo2d->Draw(“SURF3 pol”);[/code]

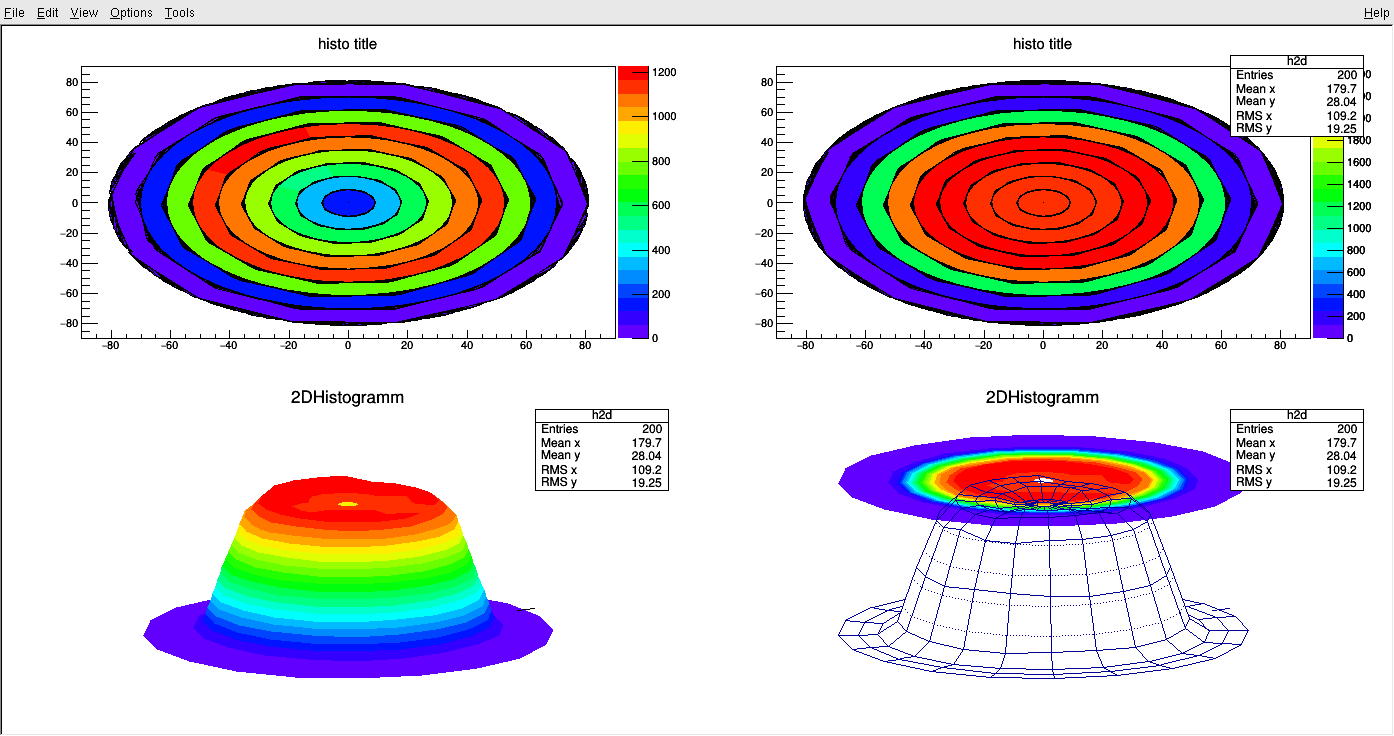
And I get these plots:

plots.png1394×736 27.5 KB

As you can see there are still some issues with the graphical representation. While the rebinning works fine, I’d like to use 2D projection of the color map in SURF 3 without the 3D grid, is this possible? Also in the SURF options it doesn’t plot the bins for r=0 (the white hole), while it does for the COLZ option.

4

All the possible option are listed here:
root.cern.ch/doc/master/classTH … .html#HP18

may be try “SURF5 POL”

5

[quote=“couet”][quote]
I’d like to use 2D projection of the color map in SURF 3 without the 3D grid
[/quote]

All the possible option are listed here:
root.cern.ch/doc/master/classTH … .html#HP18

may be try “SURF5 POL”[/quote]

SURF5 doesn’t work with POL unfortunately.

6

ok. So the only way will be to make the line color transparent.
histo->SetLineColorAlpha(kBlue, 0.35);
See the doc and limitations here:
root.cern.ch/doc/master/classTColor.html#C06

7

If I use this, i get the following error message:

Can't call TH2F::SetLineColorAlpha(kBlue,0.35) in current scope polar_gauss.cc:106: Possible candidates are... (in TH2F) (in TH2) (in TH1) *** Interpreter error recovered ***

8

because your ROOT version is too old.

9

Oh, I see, got it to work now. Thanks for the help!