Should we use integral method in TF1 or GetBinContent method in TH1 to get the integral from overlapping Gaussian peaks?
Should we find the total counts under, for instance, the Gaussian peaks analytically via fitted functions or numerically via bin content? Which is more trustworthy?
TF1::Integral always requires two parameters that explicitly set the limits of integration.
I have a question. When we get the total count from a histogram directly within a specified bin range, most of the time we get troubles to calculate the net area under the gamma-ray peaks with Gaussian like shape. I know many ways to do it, but I won’t mention them for the point I wanna make.
I guess and believe that we do not have the same overlapping problem due to adjacent peaks if we use Gaussian function fitted on the data. The reason for that is the fitted function doesn’t know if there is a contaminant part coming from the right or left neighbouring peak. It’s just a mathematical function to represents the peak as if there was only one clean peak in the histogram without anybody bothering it.
How do you feel about my argument?
Cheers.
If you have two overlapping peaks, then you need a fit function that has two Gaussians (plus some “background” model, if needed).
You may have an opinion about this idea, can you share it with me ? @moneta
The answer to your question depends on what you want to know.
If you are interested to the total number of events produced by a certain process that gives you the peak in your spectrum, you would need to model it with a function (e…g a Gaussian), together with all the other possible contributions (background, other peak contaminations, etc…) and then fit your data. From the result of the fit you will get the correct contributions.
If you are interested only in the number of events in a given range then you can use the histogram counts.
Lorenzo
Dear Lorenzo,
That’s a fair answer. I think you may guess what I want it from my plot. Of course, I want the net count under the peak in the end of the day. Of course, I will assume, for the sake of the argument, that my function will be Gaussian for the peak, and it might be 1st or 2nd order polynomial function for the background. This is again for the sake of argument and as an example to discuss deeper. In reality, nobody knows how to represent the background because the contribution from too many possibilities are overwhelmed. I won’t discuss it now in here.
What you said is correct about the total count in the last sentence if it was the case I want.
Now, I ask the question again in a different way:
Let’s check the spectrum, real data, above. On purpose, I set the coverage factor about 2.326 sigma which represents roughly 97.99% confidence limit of the actual area under the peaks. Normally, if you wanna do your analysis numerically via the bin contents from directly your histogram, then you should set those limits where you will be confident that you do not have a contribution from the adjacent peak. It’s because, again, there is no way you will know how much of these contribution belongs to 1st or the 2nd peak in the histogram.
However, if you chose to work with your model function ; such as Gaussian and polynomials, then I wanna make sure if the area under the fitted function of the Gaussian, for instance, for the first peak still has this contribution. I know it does because it 's not randomly fitted at all, it is actually a representation of the real data which initially built in terms of a histogram. Therefore. no matter you use histogram or a function, you have to plug in these extra coverage factor and intervals to retrieve 100% of the actual data. Of course, along the way, you do your estimated background subtraction.
The problem is that I haven’t seen anybody doing this properly when I was doing my ph.d long time ago. When I look at the Integral(double x1, double x2) method in ROOT, it doesn’t include this detail as well. Thus you need to manually take care of yourself like I do in the code if you remember.
My point is that you cannot find the pure uncontaminated area of the first peak if you didn’t set your coverage limit narrow enough where you haven’t started to see the 2nd peak is overlapping yet. I think defining 2 Gaussians and 1 or 2 polynomial background to fit on a data may not be enough or cannot represent the fact I discuss here. Do you think when you just call the integral method no matter how wide you set the range for the 1st peak, you will have 100% of it area without any contribution in this example!
I know mathematically how to find every single bit of the partition in the area overlaps in this example by using the integral. However, my explanation is how to do it by means of coding in ROOT nicely.
In conclusion, can you state if you agree, or can you tell me which bit you didn’t understand, or which part you disagree?
Cheers.
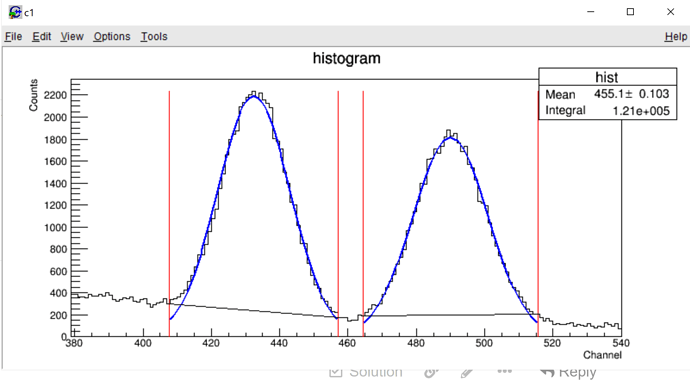
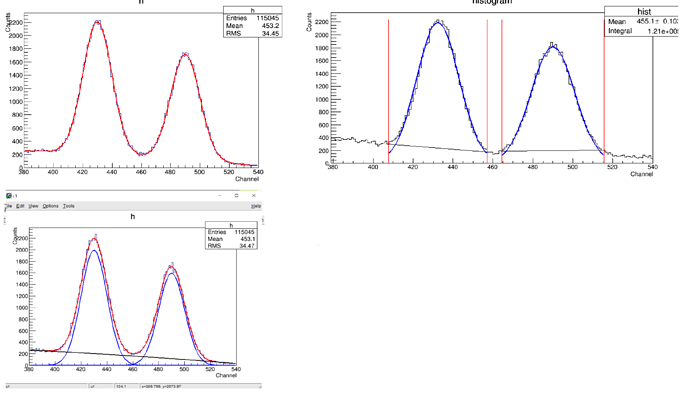
Play with a simple, dedicated simulation (a “toy MC”).
{
Bool_t bg_pol2 = kFALSE; // simulate a "pol2" or a "broken line" background
// gRandom->SetSeed(0); // make it "really random"
// gStyle->SetOptFit(); // print fit parameters in the statistics box
ROOT::Math::MinimizerOptions::SetDefaultMinimizer("Minuit2");
Int_t n = 200; // number of bins
Double_t xl = 360., xr = xl + n; // make sure "bin width" = 1.
TF1 *bg;
if (bg_pol2) bg = new TF1("bg", "pol2", xl, xr); // pol2 background
else bg = new TF1("bg", "((x < [2]) * [1] * (x - [2])) + [0]", xl, xr); // "broken line" background
bg->SetParNames("a", "b", "c"); // any background
bg->SetLineColor(kBlack); bg->SetNpx(3 * n); // e.g., (n) or (3 * n);
TF1 *g1 = new TF1("g1", "gausn", xl, xr);
g1->SetParNames("Area_1", "Mean_1", "Sigma_1"); // gausn
g1->SetLineColor(kGreen); g1->SetNpx(bg->GetNpx());
TF1 *g2 = new TF1("g2", "gausn", xl, xr);
g2->SetParNames("Area_2", "Mean_2", "Sigma_2"); // gausn
g2->SetLineColor(kBlue); g2->SetNpx(bg->GetNpx());
if (bg_pol2) {
bg->SetParameters(450., 0.4, -0.002); // pol2 background
// bg->SetParameters(1150., -2., 0.); // pol2 background
} else {
bg->SetParameters(60., -4., 460.); // "broken line" background
}
g1->SetParameters(5.e4, 430., 10.); // gausn
g2->SetParameters(4.e4, 490., 10.); // gausn
delete gDirectory->FindObject("h"); // prevent "memory leak"
TH1D *h = new TH1D("h", "h;Channel;Counts", n, xl, xr);
h->FillRandom("bg", Int_t(bg->Integral(xl, xr) + 0.5)); // any background
h->FillRandom("g1", Int_t(g1->Integral(xl, xr) + 0.5)); // gausn
h->FillRandom("g2", Int_t(g2->Integral(xl, xr) + 0.5)); // gausn
TF1 *f = new TF1("f", "g1 + g2 + bg", xl, xr); // note: parameters are (re)ordered lexicographically
f->SetLineColor(kRed); f->SetNpx(bg->GetNpx());
// f->Print();
#if 1 /* 0 or 1 */
h->Fit(f, "L"); // e.g., "" or "L"
#else /* 0 or 1 */
h->Draw();
f->Draw("same");
#endif /* 0 or 1 */
bg->SetParameters(f->GetParameter("a"), f->GetParameter("b"), f->GetParameter("c")); // any background
g1->SetParameters(f->GetParameter("Area_1"), f->GetParameter("Mean_1"), f->GetParameter("Sigma_1")); // gausn
g2->SetParameters(f->GetParameter("Area_2"), f->GetParameter("Mean_2"), f->GetParameter("Sigma_2")); // gausn
bg->Draw("same");
g1->Draw("same");
g2->Draw("same");
}
{
Bool_t bg_pol2 = kFALSE; // simulate a "pol2" or a "broken line" background
// gRandom->SetSeed(0); // make it "really random"
// gStyle->SetOptFit(); // print fit parameters in the statistics box
ROOT::Math::MinimizerOptions::SetDefaultMinimizer("Minuit2");
Int_t n = 200; // number of bins
Double_t xl = 360., xr = xl + n; // make sure "bin width" = 1.
delete gDirectory->FindObject("h"); // prevent "memory leak"
TH1D *h = new TH1D("h", "h;Channel;Counts", n, xl, xr);
TF1 *f;
if (bg_pol2) {
f = new TF1("f", "gausn(0) + gausn(3) + pol2(6)", xl, xr);
f->SetParNames("Area_1", "Mean_1", "Sigma_1", // gausn(0)
"Area_2", "Mean_2", "Sigma_2", // gausn(3)
"a", "b", "c"); // pol2(6)
f->SetParameters(5.e4, 430., 10., // gausn(0)
4.e4, 490., 10., // gausn(3)
450., 0.4, -0.002); // pol2(6)
// 1150., -2., 0.); // pol2(6)
} else {
f = new TF1("f", "gausn(0) + gausn(3) + ((x < [8]) * [7] * (x - [8])) + [6]", xl, xr);
f->SetParNames("Area_1", "Mean_1", "Sigma_1", // gausn(0)
"Area_2", "Mean_2", "Sigma_2", // gausn(3)
"a", "b", "c"); // "broken line" background (6)
f->SetParameters(5.e4, 430., 10., // gausn(0)
4.e4, 490., 10., // gausn(3)
60., -4., 460.); // "broken line" background (6)
}
f->SetLineColor(kRed); f->SetNpx(3 * n); // e.g., (n) or (3 * n);
// f->Print();
h->FillRandom("f", Int_t(f->Integral(xl, xr) + 0.5));
#if 1 /* 0 or 1 */
h->Fit(f, "L"); // e.g., "" or "L"
#else /* 0 or 1 */
h->Draw();
f->Draw("same");
#endif /* 0 or 1 */
TF1 *g1 = new TF1("g1", "gausn", xl, xr);
g1->SetParNames(f->GetParName(0), f->GetParName(1), f->GetParName(2));
g1->SetParameters(f->GetParameters() + 0); // gausn(0)
g1->SetLineColor(kGreen); g1->SetNpx(f->GetNpx());
TF1 *g2 = new TF1("g2", "gausn", xl, xr);
g2->SetParNames(f->GetParName(3), f->GetParName(4), f->GetParName(5));
g2->SetParameters(f->GetParameters() + 3); // gausn(3)
g2->SetLineColor(kBlue); g2->SetNpx(f->GetNpx());
TF1 *bg;
if (bg_pol2) bg = new TF1("bg", "pol2", xl, xr);
else bg = new TF1("bg", "((x < [2]) * [1] * (x - [2])) + [0]", xl, xr);
bg->SetParNames(f->GetParName(6), f->GetParName(7), f->GetParName(8));
bg->SetParameters(f->GetParameters() + 6); // any background (6)
bg->SetLineColor(kBlack); bg->SetNpx(f->GetNpx());
bg->Draw("same");
g1->Draw("same");
g2->Draw("same");
}
Before I comment on this code, what is +0.5 addition for on that line?
Just to get the “nearest” integer.
I can see that you write the code other way around by defining the function first and creating the histogram second. That’s a clever way of teaching, noted!
Can you explain how this FillRandom part is ACTUALLY filling the bins of the histogram?
As you know f->Integral(xl, xr) part returns just to a number which is a fixed number.
Then, I will talk about other ambiguous points in this and other codes in that topic?
Search for the “FillRandom” string in the TH1 class reference and, if you are very much interested in the details, see the TH1::FillRandom source code.
Parameters
| fname | : Function name used for filling the histogram |
|---|---|
| ntimes | : number of times the histogram is filled |
| rng | : (optional) Random number generator used to sample |
The distribution contained in the function fname (TF1) is integrated over the channel contents for the bin range of this histogram. It is normalized to 1.
Getting one random number implies:
To be honest, I couldn’t get my head around it. It seems similar to int TH1::Fill(double x, double w).
It generates random number between 0 to 1 and put that in a channel, bin by bin. The frequency of that event (width), I guess, should be the same as the integral value (y value) of each x value in the function.
However, I could not understand how you did that without a for loop or something similar. I struggle about the coding part.
I redrew your functions. On the right top, you see my previous code plotting gaus function and pol1 together separately for each peak. For some reason, I get the net integral after I substract the areas from gaus to polynomial, but most people like you, ı guess, like to get it from total function where you put all functions together ( TF1 *f = new TF1(“f”, “gausn(0) + gausn(3) + pol2(6)”, xl, xr); ). Even though it says + pol2, it means subtraction happens in this sum function. That bothers me.
In your plots (left top and bottom), why you used gausn instead of gaus and why you think one pol2 represents the background for two at the same time. I think that example is a bad one, it looks like background slope is decreasing continuously and nicely from left to right with the same angle.
How? You haven’t eliminate those contribution yet. Your fit doesn’t give us any superior ability. That’s what I think and what I try to explain.
If you want to draw the fitted contributions, you should use:
h->Fit(f, "L"); // e.g., "" or "L"
g1->SetParameters(f->GetParameters() + 0); // gausn(0)
g2->SetParameters(f->GetParameters() + 3); // gausn(3)
pol2->SetParameters(f->GetParameters() + 6); // pol2(6)
I am using a “gausn” because its first parameter is the “peak’s area”, while for a “gaus”, it is the “peak’s height”.
My “toy MC” uses a simple “pol2” function to simulate the background. When fitting experimental data, you may need to use a better model (it’s up to you to define it).
BTW. Try to use your “previous code” to analyze the newly created “h” histogram (and compare the obtained results with the actual parameters that were set).
Dear @spyhunter01
A short answer to your long message, the correct way to handle this case is to model all your contributions and then fit them to your observed data.
You should in particular include as fit parameter the integral of your signal function (or equivalent, the expected number of signal events).
In ROOT you should use the TF1NormSum class for this or the gauss function, or in case of complex modelling, I would recommend to use RooFit, which provides all the ingredients for dealing with contributions of multiple components
Lorenzo
You need to describe in your fit model all the contributions that you have in the observed data