RooProdPdf fails during a default fit

[aaronsw]

Hi, I spent a while rediscovering the bug reported here: RooProdPdf v's RooEffProd.

I have a quick example to show that the issue is still there: demo.py (1.5 KB). What happens is that a RooProdPdf fails to fit properly, as shown in the attached plot. The blue line is a RooAddPdf, and the red line is a RooProdPdf, both fit to the same data and both roughly representing the same function.

The work around is to add RooFit.Optimize(1) to the fitTo() call, but this looses some flexibility and generality. I think this bug may be particularly dangerous if a RooProdPdf is a small component of a larger PDF.

[StephanH]

Hi,

I had a look at your example.

• The first problem I fixed is that the PDFs you defined can be negative. Since that’s not possible for a PDF, RooFit will try to force Migrad away from these parameter values, giving it some headaches when minimising. Defining the functions such that they stay positive gets rid of the fit errors.

w.factory("EXPR:source('1',x)")
w.factory("EXPR:target('x',x)")
w.factory("EXPR::funcSum('a0+x*c0',x,c0[0.,10], a0[0,1])")
w.factory("EXPR::funcProd('a1+x*d0',x,d0[0.,10], a1[0,1])")
w.factory("PROD::productModel(funcProd,source)")
w.factory("SUM::sumModel(funcSum)")

• The RooAddPdf was constructed wrongly:

w.factory("SUM::sumModel(funcSum,source)")

should be

w.factory("SUM::sumModel(source*funcSum)")

This might look counter intuitive given it’s called sum, but you supply a product.

• The above still won’t fit, though, since this switches on an extended PDF whose integral is forced to be 1. To only fit the shapes (and not the normalisation), what you actually need to do is therefore:

w.factory("SUM::sumModel(funcSum)")

After those changes, this is what I get:

Nevertheless, you are right that the bug you mentioned should be taken care of. I raised the priority of the bug report.

[RongkunWang]

Ciao Aaron!

Randomly looking through forum and saw this interesting thread.

You actually get this error when you try to construct sumModel:

ERROR:InputArguments – RooAddPdf::RooAddPdf(sumModel) number of pdfs and coefficients inconsistent, must have Npdf=Ncoef or Npdf=Ncoef+1

SUM::sumModel(a , b ) is expecting the 1 or 2 RooRealVar expression for normalization. So in this case, sumModel is still funcSum because of the error.

If you really want to do

# fit sumModel (1+funcSum) to data,
instead of

w.factory(“EXPR::funcSum(‘0.1+x*c0’,x,c0[-10, 10])”);

you might want to use

w.factory(“EXPR::funcSum(‘1.1+x*c0’,x,c0[-10, 10])”);

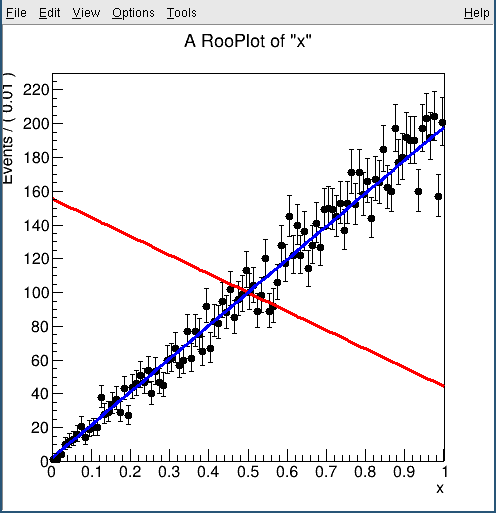
the sum of PDF that you write does not do what you want, and the one below is a uniform distribution added by a linear, the fit result is f1=1, which means the fitting of f1 is correct because the true shape is y=x

w.factory(“SUM::sumModel(f1[0,1]*funcSum, source)”)

Also, this function shape is actually very interesting. Because the true function form is y=x, while the the function looks like (c0x + 0.1) * N, where (c0 / 2+0.1) * N = 10000, the number of data is
(integral == normalization) requirement. N is like a free floating parameter. So, in order to get the best fit result, it’s actually preferable to make c0 as large as possible. One can argue that your fitting range is incorrect because it hit the limit:

NO. NAME VALUE ERROR STEP SIZE VALUE
1 c0 1.00000e+01 1.15214e+00 1.46417e-02 1.57078e+00
WARNING - - ABOVE PARAMETER IS AT LIMIT.

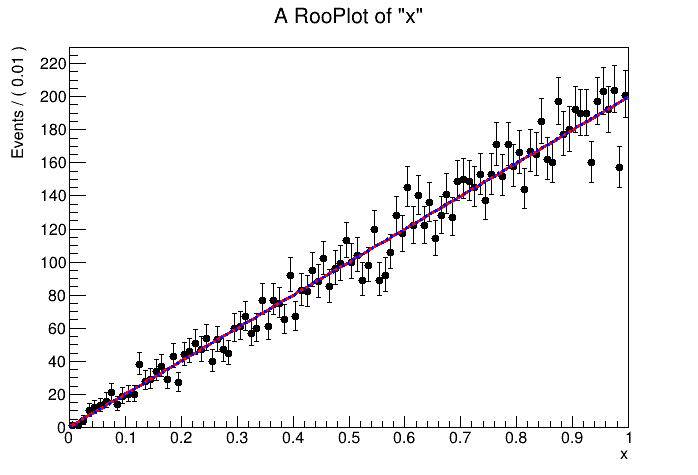
If you extend your c0 and d0 upper limit to 10,000, the two all gets good convergence.

So, this model is actually not stable, because no matter how you change your slope, you can almost always fit well with a large slope, and converge within some local minimum. It would be interesting to do a NLL scan of c0, which might show a very ragged shape with many local minima. The best fit value is essentially fitting to fluctuation.

As for why in the same case the production is worse than SUM, I have to guess it has sth to do with how NLL treats those constant terms, if the normalization is done before taking log those constant terms will enter NLL, etc etc…

Btw, I don’t think you need do overwrite: x = w.var("x"), at least not in C.
And data can take the place of target = w.obj("target_hist") ?

Best,
Rongkun