Dear all,
I am implementing a toy MC study for a model with two signals and a background:
Nexp = f1 * sgn1 + f2 * sgn2 + (1 - f1 -f2)*bkg
where the background is affected by a shape systematic through a nuisance parameter alpha.
I have constraints on both alpha and on the signal fractions: the constraint on alpha is a simple gaussian and the one on the fractions is a two dimensional gaussian with correlation (this is implemented through a RooMultiVarGausssian). To perform the toy MC experiments through RooMCStudy, and taking into account the constraints, I am following the prescriptions of this tutorial:
https://root.cern/doc/master/rf804__mcstudy__constr_8C.html
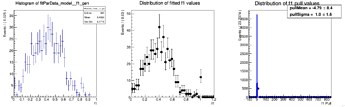
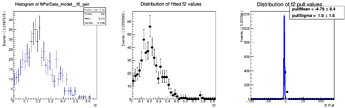
The problem I have is appearing when some of the toys are produced with “unphysical” values of the fractions (i.e. f1 + f2 > 1): here is a printout of one of these toys
1) RooRealVar:: alpha = 5 +/- 0.00609041
2) RooRealVar:: f1 = 1 +/- 0.000510215
3) RooRealVar:: f2 = 0.763207 +/- 0.00668681
4) RooRealVar:: NLL = 6975.17
5) RooRealVar:: ngen = 2000
6) RooRealVar:: alpha_gen = 1.53497 +/- 0.0663869
7) RooRealVar:: f1_gen = 0.79024 +/- 0.0061129
8) RooRealVar:: f2_gen = 0.468616 +/- 0.00518298
9) RooRealVar:: alphaerr = 0.00609041
10) RooRealVar:: alphapull = 568.932
11) RooRealVar:: f1err = 0.000510215
12) RooRealVar:: f1pull = 411.121
13) RooRealVar:: f2err = 0.00668681
14) RooRealVar:: f2pull = 44.0556
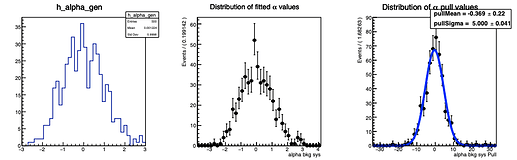
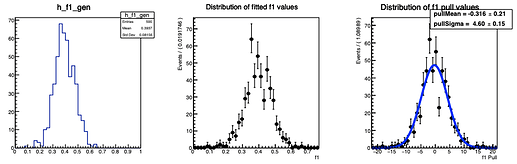
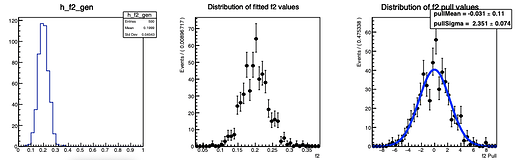
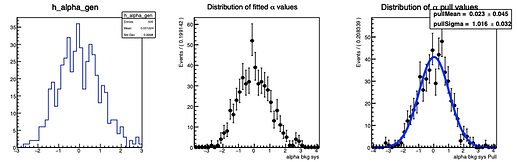
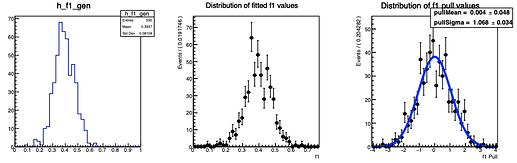
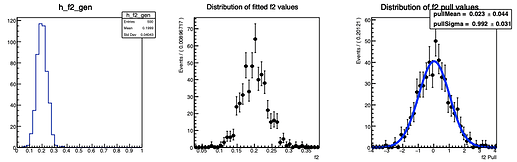
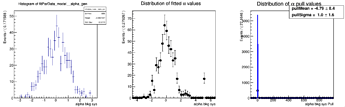
Here are the distributions I get on the parameters:
The question I have is: is there a way to configure RooMCStudy in order to reject these unphysical toys? Should I hadd some more constraints on the model?
The only solution I can think off is to write custom code deriving from RooAbsMCStudyModule to reject the unphysical values for the fractions.
Here is the code I am using:
void test_toy()
{
// signal 1
TH1F* hsgn1 = new TH1F("hsgn1","signal 1", 20, 0, 100);
TF1* g = new TF1("g","[0]*exp(-(x-[1])^2/(2*[2]^2))", 0, 100);
g -> SetParameters(100, 50, 10);
hsgn1 -> FillRandom("g", 100000);
// signal 2
TH1F* hsgn2 = new TH1F("hsgn2","signal 2", 20, 0, 100);
g -> SetParameters(100, 70, 10);
hsgn2 -> FillRandom("g", 100000);
// background
TH1F* hbkg_nom = new TH1F("hbkg_nom","nominal bkg", 20, 0, 100);
TF1* fe = new TF1("fe","[0]*exp(-[1]*x)", 0, 100);
fe -> SetParameters(50, 0.02);
hbkg_nom -> FillRandom("fe", 100000);
TH1F* hbkg_p = new TH1F("hbkg_p","+1 sigma bkg", 20, 0, 100);;
fe -> SetParameters(55, 0.03);
hbkg_p -> FillRandom("fe", 150000);
TH1F* hbkg_m = new TH1F("hbkg_m","-1 sigma bkg", 20, 0, 100);;
fe -> SetParameters(45, 0.01);
hbkg_m -> FillRandom("fe", 500000);
// define observables
RooRealVar e{"e", "energy", 0, 100, "MeV"};
e.setBins(Int_t(20));
// signal pdf
hsgn1 -> Scale(1./hsgn1 -> Integral());
RooDataHist dh_sgn1{"dh_sgn1", "dh_sgn1", RooArgSet{e}, hsgn1};
RooHistPdf sgn1("sgn1", "sgn1", RooArgSet{e}, dh_sgn1);
hsgn2 -> Scale(1./hsgn2 -> Integral());
RooDataHist dh_sgn2{"dh_sgn2", "dh_sgn2", RooArgSet{e}, hsgn2};
RooHistPdf sgn2("sgn2", "sgn2", RooArgSet{e}, dh_sgn2);
// background pdf
//
// nominal value
hbkg_nom -> Scale(1./hbkg_nom -> Integral());
RooDataHist dh_bkg_nom{"dh_bkg_nom", "dh_bkg_nom", RooArgSet{e}, hbkg_nom};
RooHistPdf bkg_0("bkg_0", "bkg_0", RooArgSet{e}, dh_bkg_nom);
//
// bkg +1 sigma
hbkg_p -> Scale(1./hbkg_p -> Integral());
RooDataHist dh_bkg_p{"dh_bkg_p", "dh_bkg_p", RooArgSet{e}, hbkg_p};
RooHistPdf bkg_p("bkg_p", "bkg_p", RooArgSet{e}, dh_bkg_p);
//RooHistFunc bkg_p("bkg_p", "bkg_p", RooArgSet{e}, dh_bkg_p);
//
// bkg -1 sigma
hbkg_m -> Scale(1./hbkg_m -> Integral());
RooDataHist dh_bkg_m{"dh_bkg_m", "dh_bkg_m", RooArgSet{e}, hbkg_m};
RooHistPdf bkg_m("bkg_m", "bkg_m", RooArgSet{e}, dh_bkg_m);
//
// build interpolation between -1 -> +1 sigma
RooRealVar alpha{"alpha", "alpha bkg sys", 0, -5, 5};
PiecewiseInterpolation bkg_sys("bkg_sys", "bkg_sys", bkg_0, bkg_m, bkg_p, alpha);
// build model
double f1_val = 0.4;
double f2_val = 0.2;
RooRealVar f1{"f1", "f1", f1_val, 0, 1};
RooRealVar f2{"f2", "f2", f2_val, 0, 1};
RooRealSumPdf sb{"sb", "sb", RooArgSet(sgn1, sgn2, bkg_sys), RooArgList(f1, f2)};
// introduce alpha constraint
RooGaussian gaus_alpha("gaus_alpha", "gaus_alpha", alpha, RooFit::RooConst(0), RooFit::RooConst(1));
// introduce f1, f2 constraint
TMatrixDSym Vf(2);
double sigma_f = 0.04;
Vf(0,0) = sigma_f;
Vf(1,1) = sigma_f/2.;
Vf(0,1) = -0.02*sigma_f*sigma_f/2.;
RooMultiVarGaussian mgaus_f("c_Vf", "c_Vf", RooArgList(f1, f2), RooArgList(RooFit::RooConst(f1_val), RooFit::RooConst(f2_val)), Vf);
RooProdPdf model{"model", "model", RooArgList(sb, gaus_alpha, mgaus_f)};
// Example of single experiment
//
alpha.setVal(2);
RooDataHist* data = model.generateBinned(RooArgSet{e}, 15000, RooFit::Verbose(1));
TCanvas* c = new TCanvas();
c->cd();
auto frame = e.frame(RooFit::Title("Before fit"));
data->plotOn(frame);
model.plotOn(frame, RooFit::LineColor(6));
model.plotOn(frame, RooFit::LineColor(2), RooFit::Components("sgn1"));
model.plotOn(frame, RooFit::LineColor(44), RooFit::Components("sgn2"));
model.plotOn(frame, RooFit::LineColor(4), RooFit::Components("bkg_sys"));
frame -> Draw();
// fit
f1.setVal(f1_val+0.05);
f2.setVal(f2_val+0.05);
alpha.setVal(0.0);
//alpha.setConstant(kTRUE);
auto fitres = model.fitTo(*data, RooFit::Constrain(RooArgSet(alpha, f1, f2)), RooFit::Save());
fitres->Print();
TCanvas* c1 = new TCanvas();
c1->cd();
auto frame1 = e.frame(RooFit::Title("After fit"));
data->plotOn(frame1);
model.plotOn(frame1, RooFit::LineColor(6));
model.plotOn(frame1, RooFit::LineColor(2), RooFit::Components("sgn1"));
model.plotOn(frame1, RooFit::LineColor(44), RooFit::Components("sgn2"));
model.plotOn(frame1, RooFit::LineColor(4), RooFit::Components("bkg_sys"));
frame1 -> Draw();
// Toy MC (from tutorial https://root.cern/doc/master/rf804__mcstudy__constr_8C.html)
//
// Perform toy study with internal constraint on alpha, f1 and f2
f1.setVal(f1_val);
f2.setVal(f2_val);
RooMCStudy mcs(model, e, RooFit::Constrain(RooArgSet(alpha, f1, f2)), RooFit::Silence(), RooFit::Binned(), RooFit::FitOptions(RooFit::PrintLevel(-1)));
// Run 500 toys of 2000 events.
// Before each toy is generated, a value for alpha, f1 and f2 is sampled from the constraint pdfs and
// that value is used for the generation of that toy.
mcs.generateAndFit(500, 2000);
// Make plot of distribution of generated value of alpha parameter
TH1 *h_alpha_gen = mcs.fitParDataSet().createHistogram("alpha_gen", -40);
// Make plot of distribution of fitted value of alpha parameter
RooPlot *frame2 = mcs.plotParam(alpha, RooFit::Bins(40));
frame2 -> SetTitle("Distribution of fitted #alpha values");
// Make plot of pull distribution on alpha
RooPlot *frame3 = mcs.plotPull(alpha, RooFit::Bins(40), RooFit::FitGauss());
frame3 -> SetTitle("Distribution of #alpha pull values");
TCanvas *c2 = new TCanvas("mcstudy_alpha_constr", "mcstudy_alpha_constr", 1200, 400);
c2 -> Divide(3);
c2 -> cd(1);
gPad -> SetLeftMargin(0.15);
h_alpha_gen -> GetYaxis() -> SetTitleOffset(1.4);
h_alpha_gen -> Draw();
c2 -> cd(2);
gPad -> SetLeftMargin(0.15);
frame2 -> GetYaxis() -> SetTitleOffset(1.4);
frame2 -> Draw();
c2 -> cd(3);
gPad -> SetLeftMargin(0.15);
frame3 -> GetYaxis() -> SetTitleOffset(1.4);
frame3 -> Draw();
// Make plot of distribution of generated value of f1 parameter
TH1 *h_f1_gen = mcs.fitParDataSet().createHistogram("f1_gen", -40);
double f1pull(0), f2pull(0);
for(auto t=0; t<500; t++)
{
cout << "\nN TOY = " << t << "\n" << endl;
f1pull = mcs.fitParDataSet().get(t)->getRealValue("f1pull");
f2pull = mcs.fitParDataSet().get(t)->getRealValue("f2pull");
if( f1pull > 50 || f2pull > 50 )
cout << "\nPROBLEM\n" << endl;
mcs.fitParDataSet().get(t)->Print("V");
}
// Make plot of distribution of fitted value of f1 parameter
RooPlot *frame4 = mcs.plotParam(f1, RooFit::Bins(40));
frame4 -> SetTitle("Distribution of fitted f1 values");
// Make plot of pull distribution on f1
RooPlot *frame5 = mcs.plotPull(f1, RooFit::Bins(40), RooFit::FitGauss());
frame5 -> SetTitle("Distribution of f1 pull values");
TCanvas *c3 = new TCanvas("mcstudy_f1_constr", "mcstudy_f1_constr", 1200, 400);
c3 -> Divide(3);
c3 -> cd(1);
gPad -> SetLeftMargin(0.15);
h_f1_gen -> GetYaxis() -> SetTitleOffset(1.4);
h_f1_gen -> Draw();
c3 -> cd(2);
gPad -> SetLeftMargin(0.15);
frame4 -> GetYaxis() -> SetTitleOffset(1.4);
frame4 -> Draw();
c3 -> cd(3);
gPad -> SetLeftMargin(0.15);
frame5 -> GetYaxis() -> SetTitleOffset(1.4);
frame5 -> Draw();
// Make plot of distribution of generated value of f2 parameter
TH1 *h_f2_gen = mcs.fitParDataSet().createHistogram("f2_gen", -40);
// Make plot of distribution of fitted value of f2 parameter
RooPlot *frame6 = mcs.plotParam(f2, RooFit::Bins(40));
frame6 -> SetTitle("Distribution of fitted f2 values");
// Make plot of pull distribution on f2
RooPlot *frame7 = mcs.plotPull(f2, RooFit::Bins(40), RooFit::FitGauss());
frame7 -> SetTitle("Distribution of f2 pull values");
TCanvas *c4 = new TCanvas("mcstudy_f2_constr", "mcstudy_f2_constr", 1200, 400);
c4 -> Divide(3);
c4 -> cd(1);
gPad -> SetLeftMargin(0.15);
h_f2_gen -> GetYaxis() -> SetTitleOffset(1.4);
h_f2_gen -> Draw();
c4 -> cd(2);
gPad -> SetLeftMargin(0.15);
frame6 -> GetYaxis() -> SetTitleOffset(1.4);
frame6 -> Draw();
c4 -> cd(3);
gPad -> SetLeftMargin(0.15);
frame7 -> GetYaxis() -> SetTitleOffset(1.4);
frame7 -> Draw();
}
Thanks for your help.
 )
)