Hi, I have a problem with constraints and would be very grateful for comments and corrections:
Situation:
I perform an extended, unbinned likelihood fit over ~5000 evts with 2 observables and a SUM-PDF of 20 components + 1 signal. There’s overlap between some backgrounds and the signal, so I am using constraints. The last step is a hypothesis test with the RooStats HypoTestInverter class to get an upper 90% C.L. limit on my signal.
Problem:
For all of my nuisance parameters I can calculate (by fitting sidebands and extrapolating) how many evts I expect in the data. This number can be as small as 1e-6 up to tens of evts. As the underlying data is the result of Poisson processes, I thought of using a Poisson PDF for the constraint.
Questions:
[ol]
[li] is a Poisson PDF the right one to use? Or should I use Gaussian constraints[/li]
[li] should the PDF be the discrete RooFit RooPoisson PDF or a continuous one (with an implementation of TMath::Poisson(x,µ) )?[/li]
[li] is the implementation of the global observable correct? In RooStats tutorials it is always
Gaussian(globalobs,nuisance,width) but for a Poisson PDF I believe it should be Poisson(nuisance,globalobs)[/li][/ol]
I created a minimal working example in python with a very simple model showing the basic situation (only 1d, 2 backgrounds, toy data, …):
already with this, problems occur. Fit results are completely different, depending on which constraint PDF is used (uncommented). For the discrete constraint, the fit doesn’t converge properly. And for both constraint possibilities I couldn’t perform the hypothesis test, using the ROOT StandardHypoTestInvDemo.C macro.
mwe_constraint.py (2.27 KB)
#!/usr/bin/env python
import ROOT
from ROOT import RooFit as RF
from ROOT import RooStats as RS
# Initial number of events
n_bkg1_init = 50
n_bkg2_init = 0.2
n_sig_init = 0
# Create workspace and one observable
w = ROOT.RooWorkspace("w")
x = w.factory("x[0,10]")
# Construct PDFs for signal and 2 backgrounds
sig = w.factory("Gaussian::sig(x,sig_mean[5],sig_sigma[0.5])")
bkg1 = w.factory("Polynomial::bkg1(x)")
bkg2 = w.factory("Gaussian::bkg2(x,bkg2_mean[7],bkg2_sigma[0.5])")
model = w.factory("SUM::model(n_sig[0,10]*sig,n_bkg1[0,100]*bkg1,n_bkg2[0,5]*bkg2)")
# Create constraint PDF
#constraint = w.factory("EXPR::constraint('TMath::Poisson(n_bkg2,n_bkg2_obs)',n_bkg2,n_bkg2_obs[0,10])") # continuous Poisson PDF
constraint = w.factory("Poisson::constraint(n_bkg2,n_bkg2_obs[0,5])") # discrete Poisson PDF
cmodel = w.factory("PROD::cmodel(model,constraint)")
# Initialize number of events
w.var("n_sig").setVal(n_sig_init)
w.var("n_bkg1").setVal(n_bkg1_init)
w.var("n_bkg2").setVal(n_bkg2_init)
w.var("n_bkg2_obs").setVal(n_bkg2_init)
w.var("n_bkg2_obs").setConstant()
# Generate toy event set and fit it
data = cmodel.generate(ROOT.RooArgSet(x), RF.Name("data"))
r = cmodel.fitTo(data, RF.Minimizer("Minuit2","Migrad"), RF.Strategy(2), RF.Extended(1), RF.Constrained(), RF.Save(1))
r.Print("v")
getattr(w,"import")(data)
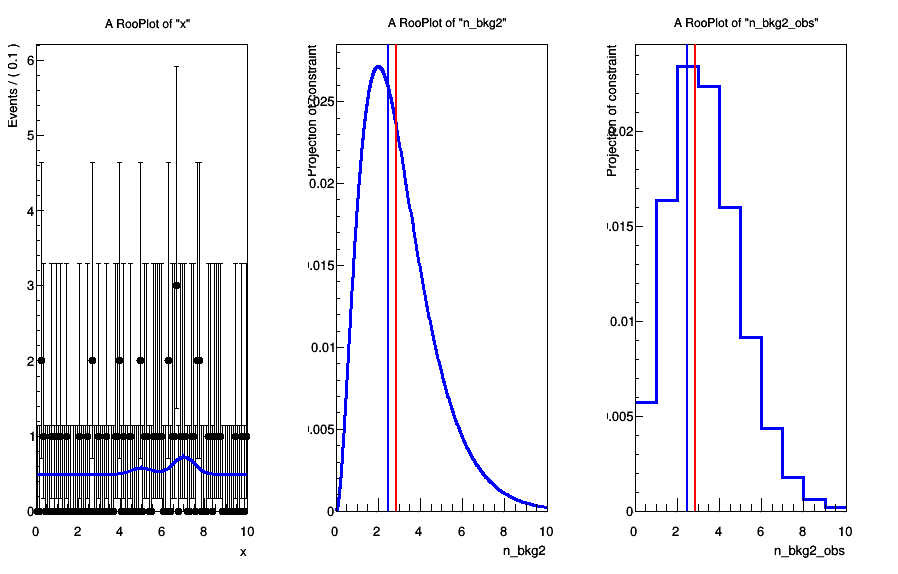
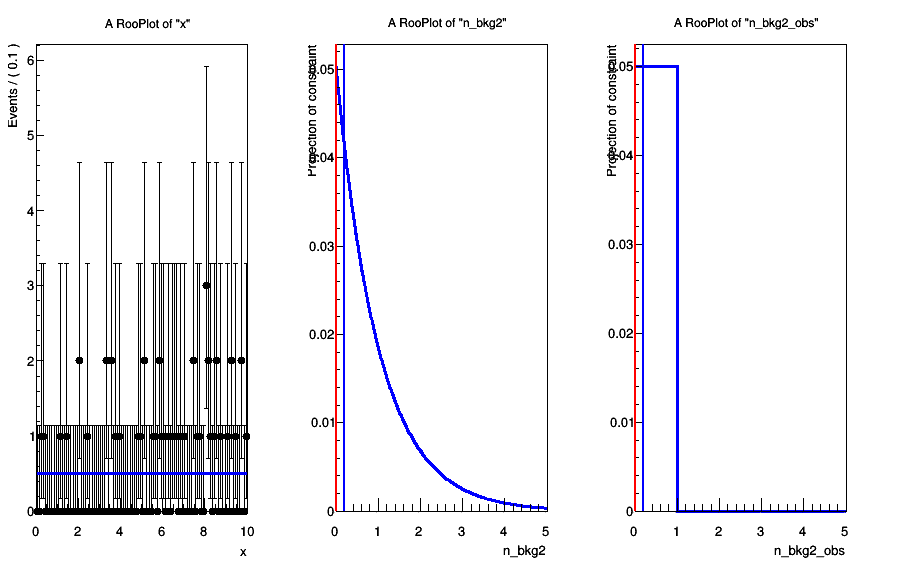
# Plot toy data with best fit PDF plus constraint PDF
c = ROOT.TCanvas()
c.Divide(2)
c.cd(1)
xframe = x.frame()
data.plotOn(xframe)
model.plotOn(xframe)
xframe.Draw()
c.cd(2)
bframe = w.var("n_bkg2").frame()
w.pdf("constraint").plotOn(bframe, RF.Precision(1e-5))
bframe.Draw()
# Draw line indicating the best fit for n_bkg2
c.Update()
line = ROOT.TLine()
line.SetLineColor(ROOT.kRed)
line.DrawLine(r.floatParsFinal().find('n_bkg2').getVal(), ROOT.gPad.GetUymin(), r.floatParsFinal().find('n_bkg2').getVal(), ROOT.gPad.GetUymax())
# Create RooStats model config and store it in workspace
mc = RS.ModelConfig("mc", w)
mc.SetPdf( cmodel )
mc.SetParametersOfInterest( ROOT.RooArgSet(w.var("n_sig")) )
mc.SetObservables( ROOT.RooArgSet(w.var("x")) )
mc.SetConstraintParameters( ROOT.RooArgSet(w.var("n_bkg2")) )
mc.SetNuisanceParameters( ROOT.RooArgSet(w.var("n_bkg1"),w.var("n_bkg2")) )
mc.SetGlobalObservables( ROOT.RooArgSet(w.var("n_bkg2_obs")) )
getattr(w,"import")(mc)
w.Print('v')