Ok great I am happy that I have been useful.
Strictly related, also RooGamma yells about negative x although it returns 0 anyways. The source is TMath::GammaDist, which does that.
However I would like to ask for more help because a similar problem seems to occur again during the fitting procedure. It is a long post summarizing my attempts and investigation of the last weeks, but just before the Christmas holiday it is meant to be discussed (hopefully) only on next year when I am also back from holidays (I will make sure that it does not get closed in the first week of January)
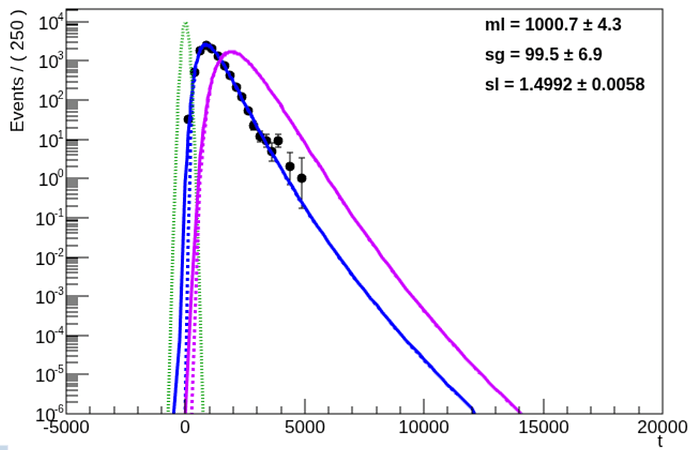
I have build up a model composing either a set of log-normal distributions or a set gamma distributions (convoluted with resolution gaussian etc)
// Model for the case of log-normal peaks model
RooRealVar nbkg("nbkg","background events",300000,1.,1000000.) ;
RooRealVar nsig("nsig","signal events",15000,1.,100000.) ;
RooRealVar fdouble("fdouble","fraction of double to single events",0.02,0.001,0.1) ;
RooFormulaVar ndouble("ndouble","nsig*fdouble",{nsig,fdouble}) ;
RooRealVar fd1miss("fd1miss","fraction of d1 miss to single events",0.3,0.001,0.8) ;
RooFormulaVar nd1miss("nd1miss","nsig*fd1miss",{nsig,fd1miss}) ;
RooAddPdf model("model","model",
RooArgList(gauss,lnxg,lnxlnxg,lognormal_u),
RooArgList(nbkg,nsig,ndouble,nd1miss)) ;
From the “old 2009” RooFit manual, I understand that when the number of coefficients is the same of the number of component pdfs, the model is assumed an extended pdf model with coefficients used as events count rather than probability fractions. Therefore an extended likelihood is built for fitting procedures, which is fine, it is what I want.
I believe that I have set reasonable starting values:
and I have set small errors on parameters to ensure that Minuit does not immediately jumps away from here.
However any fit attempt
std::unique_ptr<RooFitResult> roofitres {
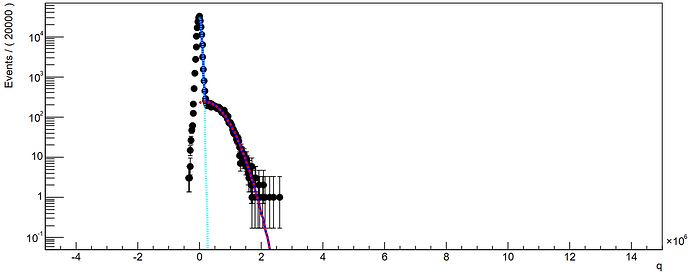
model.fitTo(spe, RooFit::Save() , RooFit::Range( -0.5,5.5) )
};
fails with a long list of:
Returning maximum FCN so far (-inf) to force MIGRAD to back out of this region. Error log follows.
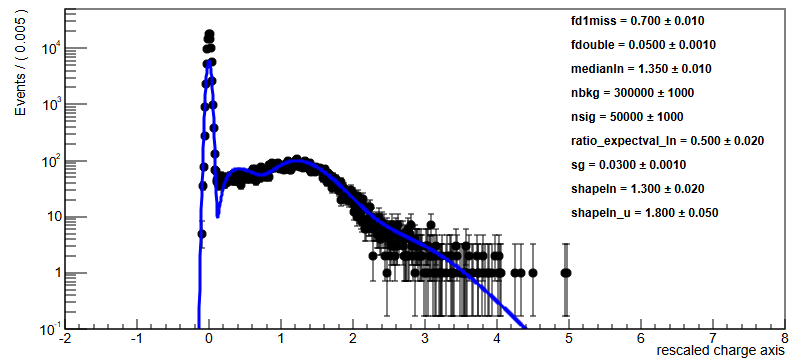
Parameter values: fd1miss=0.7 fdouble=0.05 medianln=1.35 nbkg=300000 nsig=50000 ratio_expectval_ln=0.5 sg=0.03 shapeln=1.3 shapeln_u=1.8
RooAbsPdf::lognormal_u_over_lognormal_u_Int[x][ numerator=lognormal_u denominator=lognormal_u_Int[x] ]
p.d.f value is Not-a-Number @ numerator=lognormal_u=7.61465e-06, denominator=lognormal_u_Int[x]=0.999996
[ ... same lines ... ]
RooAddPdf::model[ nbkg * gauss_over_gauss_Int[x] + nsig * lnxg_over_lnxg_Int[x] + ndouble * lnxlnxg_over_lnxlnxg_Int[x] + nd1miss * lognormal_u_over_lognormal_u_Int[x] ]
getLogVal() top-level p.d.f evaluates to NaN @ !refCoefNorm=(x = 7.5), !pdfs=(gauss_over_gauss_Int[x] = 0,lnxg_over_lnxg_Int[x] = 1.07732e-10,lnxlnxg_over_lnxlnxg_Int[x] = 1.8821e-07,lognormal_u_over_lognormal_u_Int[x] = 7.61469e-06), !coefficients=(nbkg = 300000 +/- 1000,nsig = 50000 +/- 1000,ndouble = 2500,nd1miss = 35000)
[ ... same lines ... ]
My understanding of this log is that already with the starting parameters the NLL cannot be calculated, or maybe is log(0). Maybe lines 5-8 tells that the lognormal_uis the culprit, but I do not understand what it means with the numerator and denominator values (they seems valid numbers, so the ratio should be valid too). Also !refCoefNorm=(x = 7.5) seems to suggest that calculations are made over the full range, despite the requested fit range was up to 5.5 …
To understand what is happening I build and inspect directly the constructed NLL:
auto model_nll = model.createNLL(spe, RooFit::Range(-0.5,5.5), RooFit::Extended(true));
//I tried various ranges and the Extended option true and false, although from the manual I got that the default is Extended because the composite pdf is extended
model_nll->getVal()
The last line, that should give me the NLL at the current (starting) values of the parameters, produces the same errors.
However the model has valid and non-zero values over the full range used:
for (double xval = -1. ; xval < 8. ; xval += 0.05) {
x = xval;
RooArgSet norm_set{x}; //not sure how to indicate a different x range here
cout << model.getVal({x}) << "\t" << model.getLogVal(&norm_set) << endl;
}
So I have to understand how this binned log likelihood is calculated (continue on the next post)