RooAddPdf: when to use recursiveFraction?

[kondratyevd]

Dear RooFit experts,

I am trying to implement a fit with the sum of 3 Gaussians with a 10% resolution uncertainty expressed through a single nuisance parameter (the way the resolution uncertainty is implemented is taken from the internal documentation of H→µµ analysis at CMS).

Below is my Python implementation of the model in RooFit:

# Initialize workspace and the observable variable
    w = ROOT.RooWorkspace("w", False)
    var = ROOT.RooRealVar("mass","",110,135)   
    getattr(ROOT.RooWorkspace, 'import')(w, var)

# Mean values of the Gaussians
    w.factory("mean1 [125., 120., 130.]")
    w.factory("mean2 [125., 120., 130.]")
    w.factory("mean3 [125., 120., 130.]")

# Define the value of the uncertainty
    w.factory("mu_res_unc [0.1, 0.1, 0.1]")
    w.var("mu_res_unc").setConstant(True)

# Gaussian nuisance to be set in the datacard (the value is released after fit)
    w.factory("mu_res_beta [0, 0, 0]")   

# Width parameters with resolution uncertainty
    w.factory("EXPR::width1_times_nuis('width1*(1 + mu_res_unc*mu_res_beta)',{width1[1.0, 0.5, 5.0],mu_res_unc, mu_res_beta})")
    w.factory("EXPR::width2_times_nuis('width2*(1 + mu_res_unc*mu_res_beta)',{width2[5.0, 2.0, 10.],mu_res_unc, mu_res_beta})")
    w.factory("EXPR::width3_times_nuis('width3*(1 + mu_res_unc*mu_res_beta)',{width3[5.0, 1.0, 10.],mu_res_unc, mu_res_beta})")

# Taking into account shift between mean values of Gaussians
    w.factory("expr::deltaM21('mean2-mean1',{mean2, mean1})")
    w.factory("expr::deltaM31('mean3-mean1',{mean3, mean1})")
    w.factory("EXPR::mean2_final('mean2 + mu_res_unc*mu_res_beta*deltaM21',{mean2, mu_res_unc, mu_res_beta, deltaM21})")
    w.factory("EXPR::mean3_final('mean3 + mu_res_unc*mu_res_beta*deltaM31',{mean3, mu_res_unc, mu_res_beta, deltaM31})")

# Gaussians
    w.factory("Gaussian::gaus1(mass, mean1, width1_times_nuis)")
    w.factory("Gaussian::gaus2(mass, mean2_final, width2_times_nuis)")
    w.factory("Gaussian::gaus3(mass, mean3_final, width3_times_nuis)")
    gaus1 = w.pdf("gaus1")
    gaus2 = w.pdf("gaus2")
    gaus3 = w.pdf("gaus3")

# Mixing parameters
    w.factory("mix1 [0.5, 0.0, 1.0]")
    w.factory("mix2 [0.5, 0.0, 1.0]")
    mix1 = w.var("mix1")
    mix2 = w.var("mix2")

# Summation
    smodel = ROOT.RooAddPdf('smodel', 'smodel', ROOT.RooArgList(gaus1, gaus2, gaus3) , ROOT.RooArgList(mix1, mix2), ROOT.kTRUE)

# Fit the data
    smodel.fitTo(data, ROOT.RooFit.Range("full"),ROOT.RooFit.Save(), ROOT.RooFit.Verbose(False))

# Fix the post-fit values of the parameters
    for par in  ["mean1", "mean2", "mean3", "width1", "width2", "width3", "mix1", "mix2"]:
        w.var(par).setConstant(True)

# Release the nuisance parameter
    w.var("mu_res_beta").setRange(-5, 5)
    w.var("mu_res_beta").setVal(0)

My question is about the summation of the Gaussians:

# Summation
    smodel = ROOT.RooAddPdf('smodel', 'smodel', ROOT.RooArgList(gaus1, gaus2, gaus3) , ROOT.RooArgList(mix1, mix2), ROOT.kTRUE)

According to the RooAddPdf documentation (https://root.cern.ch/doc/master/classRooAddPdf.html), the last parameter recursiveFraction defines whether the mixing parameters are interpreted as recursive fraction (and converted into RooRecursiveFraction), or not.

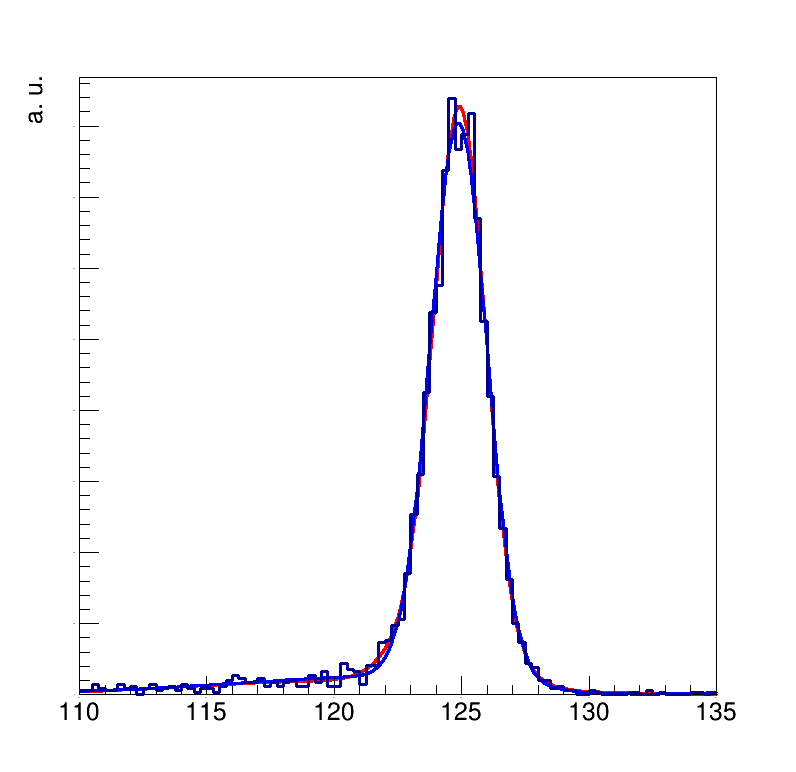
I have tried both setting recursiveFractions=ROOT.kTRUE and recursiveFractions=ROOT.kFALSE and I get slightly different fits: on the attached plot the red line corresponds to kTRUE and the blue line corresponds to kFALSE.

Can you please explain why these two options give different fits, and which option is recommended in this case?

Thanks,
Dmitry

[StephanH]

Hello Dmitry,

the difference is in how the different components are interpreted.

• True If you want a normalised PDF (no extended fit), use the recursive fractions to ensure that the coefficients sum to 1. It does not matter what how you set the coefficients, as long as they are between 0 and 1.
• False In this mode, the RooAddPdf will try to keep the sum of coefficients at 1 by setting the last coefficient to 1 - sum(coef_i), but this will fail if the sum of coefficients is already larger than 1 or exactly 1 (as in your case). In this case, the only option for the fitter is to set the coefficient for the last PDF to 0, which probably explains why the two cases differ. You should also get an error message if the sum of coefficients is larger than 1.
  If you want an extended likelihood, use this mode.

[kondratyevd]

Hello Stephan,

Indeed, if in the case recursiveFractions=kFALSE I set the initial value for the last coefficient mix2 to 0, I get the results identical to those for recursiveFractions=kTRUE.

Thanks!