Revising the Metropolis-Hastings algorithm used by MCMCCalculator

Roofit and RooStats
1

Dear All,

I have been recently using the RooStats::MCMCCalculator class to calculate an upper limit, using a model with one parameter of interest and several nuisance parameters, 11 to be specific. I realised that in the implementation of the Metropolis-Hastings algorithm that the class is using, not all the steps are saved in the Markov chain. Instead, only the points that were accepted by the algorithm are added to the chain. This becomes quite obvious when you compare the number of steps of the final Markov Chain and the number of iterations that were set initially. Also, I looked into the implementation file of the class (https://root.cern.ch/doc/v606/MetropolisHastings_8cxx_source.html) and I’m convinced now that the rejected events are not stored.

Is this correct? My understanding about the Metropolis-Hastings algorithm is that in the final step of the algorithm you either accept the candidate point, add it to the chain and move there or you stay at the current point, but you also add this point to the chain so that it is counted TWICE. Saving these extra points may be a problem at the beginning of the chain, when you haven’t reached a stable regime yet, but that’s why the burn-in steps are for.

Are you aware of this point? If so, could anyone explain what is the reason behind implementing the Metropolis-Hastings algorithm in this particular way? Has this algorithm been revised in future versions of ROOT? (I’m using 5.34.20).

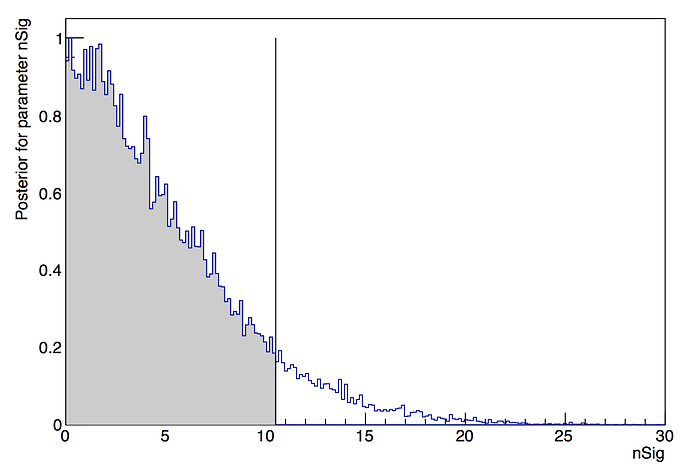
I’m not sure if it is related, but in my analysis I haven’t managed yet to get a smooth posterior distribution, even for a large number of iterations. As an example, I attach the posterior distribution that I obtain as a function of the POI for one million number of iterations, and as you can see the distribution has still some noticeable fluctuations.

Many thanks,
Ibles

Posterior_distribution.png1650×1122 40.9 KB

1 Like
2

Hi,

I think the algorithm is correct, because when a proposed point is rejected the weight is increased by one and the current point is then added to the chain with a weight equal to the number of times new points were rejected.

The fact that you see large fluctuations is exactly due to the fact that the same points might have a large weight, since the algorithm did not find better proposed points.

Best Regards

Lorenzo

3

Hi,
Thanks for the reply, that makes a lot of sense actually.
If that is the way the algorithm is constructed, I guess then it’s desirable to have a reasonable high acceptance rate, otherwise the posterior distribution will most likely have pronounced peaks.

I have been playing with different proposal functions and the highest acceptance rate I can get is around 20% using the SequentialProposal with a value of 0.2 for the fraction range. I tried with both UniformProposal and the multivariate normal distribution that you can get using the ProposalHelper and a fit to your negative log-likelihood, however the acceptance rates for these are more around the 10%.

Before closing this topic, I’d like to make sure that I’m using a good proposal function. Could anyone confirm that SequentialProposal is a good proposal function or point to me another one that in general provides a good acceptance rate (I didn’t find any extra ones apart from the other two I already mentioned)?

Best,
Ibles

4

Hi,

The SequentialProposal is a good proposal function and I think is one of the most used one for this reason (very good acceptance rate)

Best

Lorenzo

5

This topic was automatically closed 14 days after the last reply. New replies are no longer allowed.