Hi , I use the below test statistics to calculate the upper limit.
203 // profile likelihood test statistics
204 ProfileLikelihoodTestStat profll(*sbModel->GetPdf());
205 profll.SetOneSided(false);
206 // for CLs (bounded intervals) use one-sided profile likelihood
207 if (useCLs) profll.SetOneSided(true);
But I can’t understand this test statistics. it seems the -ln(ratio of likelihood).
I construct a poisson model , s = 3, b = 3 , nobs =1. And I just use this test statistics, but I find the distribution is very strange.
However I can check the black line in the plot, It is consistent with my codes, but the distribution is not consistent
Hi,
Thanks for the post.
Taking into account the presence of background in the data may result in a value of the estimator of a model parameter which is “nonphysical”. For example, observing less than the mean expected number of background events could be accommodated better if the signal cross-section was negative.
A possible strategy to treat this case is to follow the CLs prescription, introducing the so called modified, or conservative, frequentist approach. The name refers to the fact that by construction the limits to which it leads are always less aggressive with respect to the ones obtained with the CLsb quantity. This prescription consists in the normalisation of the confidence level observed for the H1 hypothesis, CLsb, with the one observed for the H0 hypothesis, CLb. The normalisation
is simply defined as CLs = CLsb/CLb .
In this way, it is possible to obtain sensible limits on the number of observed signal events even if the observed yield is so low to compel the H0 hypothesis. The CLs quantity can be seen as the signal confidence level, as if every background event would have been discarded. Even if CLs is not technically a confidence level, the signal hypothesis can be considered excluded with a certain confidence level CL when 1 − CLs < CL.
If the CLs method is not clear, a lot of literature is available about it (it’s a method which is around since decades 
used since the LEP times). I could perhaps link what I believe is the reference paper for the method, by Alex Read, https://cds.cern.ch/record/451614 .
I hope this helps.
Cheers,
D
Thanks for your reply. But I still have two question:
I have used CLs method of RooStat to calculate the upper limit of Poisson model.
for example: my poisson model is "b = 3 ,s is the POI , nobs = 1 ".
So I don’t know which test statistical I can choose. the ProfileLikelihoodTestStat or NumEventsTestStat ? Additionally the NumEventsTestStat seems can’t work, thus I just try to use
ProfileLikelihoodTestStat. I also wonder what is the defination of ProfileLikelihoodTestStat ? the -log(ratio of likelihood) ?
The second question is the toyMCsample.
my Null hypotheis is S+B poisson Model and Alt Model is B poisson Model
So I want to know how the toyMCsample get the distribution of profilelikelihood when I set the ProfileLikelihoodTestStat to the toyMCsampler. Could you give some comment about this if you know the details of these class ?
Thank you very much !
cheers
Yuxiang
This is my model config model: PoissonModelWithBackgNoUncertaity.C · main · huyuxiang@ihep.ac.cn / Intro_to_RooStat · GitLab
// make a Poisson model with signal and background
using namespace RooFit;
using namespace RooStats;
void PoissonModelWithBackgNoUncertaity(int nobs = 1, double b = 3) {
RooWorkspace w("w",true);
// make sum of s+b
w.factory("sum:nexp(s[3,0,6],b[3])");
// Poisson of (n | s+b)
w.factory("Poisson:model(nobs[1,0,50],nexp)");
RooRealVar * obs = w.var("nobs");
w.var("b")->setVal(b);
//set value of observed events
obs->setVal(nobs);
// make data set with the number of observed events
RooDataSet data("data","", *obs );
data.add(*obs );
w.import(data);
w.Print();
cout << "nobs = " << nobs << endl;
cout << "b = " << b << endl;
ModelConfig mc("ModelConfig",&w);
mc.SetPdf(*w.pdf("model"));
mc.SetParametersOfInterest(*w.var("s"));
mc.SetObservables(*w.var("nobs"));
// set an empty set since there are no nuisance parameters
mc.SetNuisanceParameters(*w.var("b"));
// these are needed for the hypothesis tests
mc.SetSnapshot(*w.var("s"));
//mc.SetGlobalObservables(*w.var("b"));
mc.Print();
// import model in the workspace
w.import(mc);
TString fileName = TString::Format("PoissonModelWithBackg_n%d.root",nobs);
// write workspace in the file (recreate file if already existing)
w.writeToFile(fileName, true);
cout << "model written to file " << fileName << endl;
}
The below is the HypoTest codes:
void HypoTestInvDemo(const char * infile = "",
const char* workspaceName = "w",
const char* modelSBName = "ModelConfig",
const char* modelBName = "",
const char* dataName = "data" )
{
TString fileName(infile);
// Check if example input file exists
TFile *file = TFile::Open(fileName);
// if input file was specified but not found, quit
if(!file ) {
cout <<"file " << fileName << " not found" << endl;
return;
}
// get the workspace out of the file
RooWorkspace* w = (RooWorkspace*) file->Get(workspaceName);
if(!w){
cout <<"workspace not found" << endl;
return;
}
RooAbsData * data = w->data(dataName);
if (!data) {
Error("StandardHypoTestDemo","Not existing data %s",dataName);
w->Print();
return;
}
// check the model taken from the workspace
ModelConfig* bModel = (ModelConfig*) w->obj(modelBName);
ModelConfig* sbModel = (ModelConfig*) w->obj(modelSBName);
if (!sbModel) {
Error("StandardHypoTestDemo","Not existing ModelConfig %s",modelSBName);
w->Print();
return;
}
// check the model
if (!sbModel->GetPdf()) {
Error("StandardHypoTestDemo","Model %s has no pdf ",modelSBName);
w->Print();
return;
}
if (!sbModel->GetParametersOfInterest() || sbModel->GetParametersOfInterest()->getSize() == 0) {
Error("StandardHypoTestDemo","Model %s has no poi ",modelSBName);
w->Print();
return;
}
if (!sbModel->GetObservables() || sbModel->GetObservables()->getSize() == 0) {
Error("StandardHypoTestInvDemo","Model %s has no observables ",modelSBName);
w->Print();
return;
}
// assume exists only one parameter of interest
RooRealVar* poi = (RooRealVar*) sbModel->GetParametersOfInterest()->first();
if (!sbModel->GetSnapshot() ) {
Info("StandardHypoTestInvDemo","Model %s has no snapshot - make one using model poi",modelSBName);
sbModel->SetSnapshot( *poi );
}
if (!bModel || bModel == sbModel) {
Info("StandardHypoTestInvDemo","The background model %s does not exist",modelBName);
Info("StandardHypoTestInvDemo","Copy it from ModelConfig %s and set POI to zero",modelSBName);
bModel = (ModelConfig*) sbModel->Clone();
bModel->SetName(TString(modelSBName)+TString("_with_poi_0"));
double oldval = poi->getVal();
poi->setVal(0);
bModel->SetSnapshot( *poi );
poi->setVal(oldval);
}
/////////////////////////////////////////////////////////////
// REAL Tutorial starts here
////////////////////////////////////////////////////////////
// build test statistics and hypotest calculators for running the inverter
// create the calculator
// create the HypoTest calculator class
// frequentist calculator
FrequentistCalculator * fc = new FrequentistCalculator(*data, *bModel, *sbModel);
fc->SetToys(2000,2000); // 1000 for null (S+B) , 50 for alt (B)
// asymptotic calculator
// AsymptoticCalculator * ac = new AsymptoticCalculator(*data, *bModel, *sbModel);
// ac->SetOneSided(true); // rof one-side tests (limits)
// AsymptoticCalculator::SetPrintLevel(-1);
// // Hybrid calculator
HybridCalculator * hc = new HybridCalculator(*data, *bModel, *sbModel);
hc->SetToys(1000,500); // 1000 for null (S+B) , 50 for alt (B)
// check for nuisance prior pdf in case of nuisance parameters
//if (sbModel->GetNuisanceParameters() && sbModel->GetNuisanceParameters()->getSize() > 0) {
// // for hybrid need nnuisance pdf
// RooAbsPdf * nuisPdf = RooStats::MakeNuisancePdf(*sbModel,"nuisancePdf_sbmodel");
// hc->ForcePriorNuisanceAlt(*nuisPdf);
// hc->ForcePriorNuisanceNull(*nuisPdf);
//}
// create hypotest inverter
// passing the desired calculator
HypoTestInverter calc(*fc);
// set confidence level
calc.SetConfidenceLevel(0.90);
// for CLS
bool useCLs = false;
calc.UseCLs(useCLs);
calc.SetVerbose(false);
// configure ToyMCSampler
ToyMCSampler *toymcs = (ToyMCSampler*)calc.GetHypoTestCalculator()->GetTestStatSampler();
// for number counting (otherwise need to use extended pdf
toymcs->SetNEventsPerToy(1);
// profile likelihood test statistics
ProfileLikelihoodTestStat profll(*sbModel->GetPdf());
profll.SetOneSided(false);
// for CLs (bounded intervals) use one-sided profile likelihood
if (useCLs) profll.SetOneSided(true);
// ratio of profile likelihood - need to pass snapshot for the alt
//RatioOfProfiledLikelihoodsTestStat ropl(*sbModel->GetPdf(), *bModel->GetPdf(), bModel->GetSnapshot());
// max likelihood
//MaxLikelihoodEstimateTestStat maxll(*sbModel->GetPdf(),*poi);
// number of events test statistics
// NumEventsTestStat nevtts;
// set the test statistic to use
toymcs->SetTestStatistic(&profll);
//toymcs->SetTestStatistic(&ropl);
//toymcs->SetTestStatistic(&nevtts);
//toymcs->SetTestStatistic(&maxll);
// control message
//RooMsgService::instance().getStream(1).removeTopic(RooFit::NumIntegration);
// suppress info and progress messages
//RooMsgService::instance().setGlobalKillBelow(RooFit::WARNING) ;
int npoints = 4; // number of points to scan
// min and max (better to choose smaller intervals)
double poimin = poi->getMin();
double poimax = poi->getMax();
//poimin = -2; poimax=4;
std::cout << "Doing a fixed scan in interval : " << poimin << " , " << poimax << std::endl;
calc.SetFixedScan(npoints,poimin,poimax);
HypoTestInverterResult * r = calc.GetInterval();
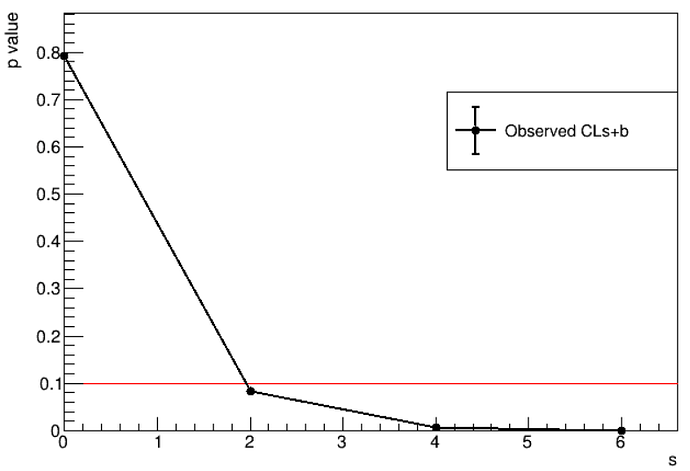
// analyze result produced by the inverter
double upperLimit = r->UpperLimit();
double ulError = r->UpperLimitEstimatedError();
// double lowerLimit = r->LowerLimit();
// double llError = r->LowerLimitEstimatedError();
// if (lowerLimit < upperLimit*(1.- 1.E-4))
// std::cout << "The computed lower limit is: " << lowerLimit << " +/- " << llError << std::endl;
std::cout << "The computed upper limit is: " << upperLimit << " +/- " << ulError << std::endl;
// compute expected limit
std::cout << "Expected upper limits, using the B (alternate) model : " << std::endl;
std::cout << " expected limit (median) " << r->GetExpectedUpperLimit(0) << std::endl;
std::cout << " expected limit (-1 sig) " << r->GetExpectedUpperLimit(-1) << std::endl;
std::cout << " expected limit (+1 sig) " << r->GetExpectedUpperLimit(1) << std::endl;
// plot now the result of the scan
HypoTestInverterPlot *plot = new HypoTestInverterPlot("HTI_Result_Plot","Feldman-Cousins Interval",r);
// plot in a new canvas with style
TCanvas * c1 = new TCanvas("HypoTestInverter Scan");
c1->SetLogy(false);
//plot->Draw("CLb"); // plot also CLb and CLs+b
plot->Draw("OBS"); // plot only observed p-value
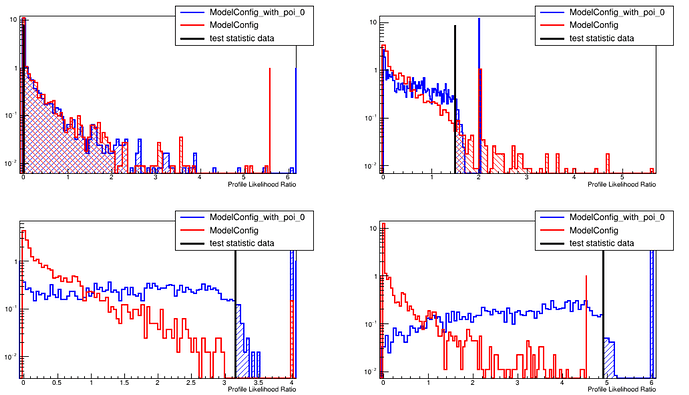
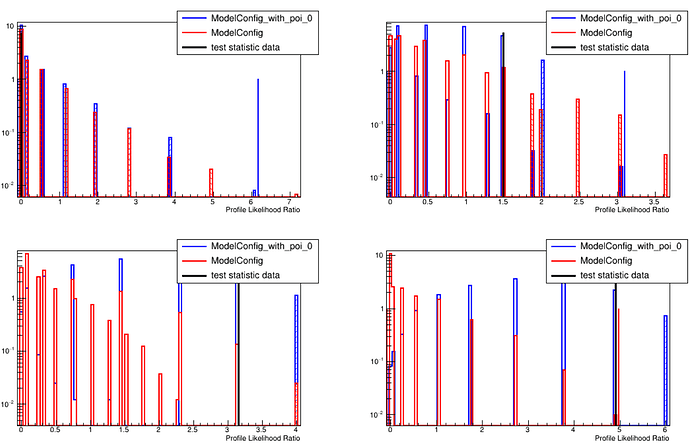
// plot also in a new canvas the test statistics distributions
// plot test statistics distributions for the two hypothesis
// when distribution is generated (case of FrequentistCalculators)
const int n = r->ArraySize();
if (n> 0 && r->GetResult(0)->GetNullDistribution() ) {
TCanvas * c2 = new TCanvas("Test Statistic Distributions","",2);
if (n > 1) {
int ny = TMath::CeilNint( sqrt(n) );
int nx = TMath::CeilNint(double(n)/ny);
c2->Divide( nx,ny);
}
for (int i=0; i<n; i++) {
if (n > 1) c2->cd(i+1);
SamplingDistPlot * pl = plot->MakeTestStatPlot(i);
pl->SetLogYaxis(true);
pl->Draw();
}
}
// optionally save result in a file
// TFile * fileOut = new TFile(mResultFileName,"RECREATE");
// r->Write();
// fileOut->Close();
delete r;
delete hc;
}
and the result is:
This topic was automatically closed 14 days after the last reply. New replies are no longer allowed.
