Problem of Using StandardHypoTestInvDemo.C to Calculate the Upper-limit of Feldman-cousins methods

[huyuxiang]

Hi,
I want to use StandardHypoTestInvDemo.C to calculate upper-limit properly but I find some difference between the result of StandardHypoTestInvDemo.C and the result of original paper of Feldman-Cousins.

The CountingModel is below:

using namespace RooFit;
using namespace RooStats;

void CountingModel(  int nobs = 3,           // number of observed events
                     double b = 1,           // number of background events
                     double sigmab = 0.01)   // relative uncertainty in b
{
   RooWorkspace w("w");
   
// make Poisson model * Gaussian constraint
   w.factory("sum:nexp(s[3,0,15],b[1,0,10])");
// Poisson of (n | s+b)
   w.factory("Poisson:pdf(nobs[0,50],nexp)");
   w.factory("Gaussian:constraint(b0[0,10],b,sigmab[1])");
   w.factory("PROD:model(pdf,constraint)");

   w.var("b0")->setVal(b);
   w.var("b0")->setConstant(true); // needed for being treated as global observables
   w.var("sigmab")->setVal(sigmab*b);  
   

   ModelConfig mc("ModelConfig",&w);
   mc.SetPdf(*w.pdf("model"));
   mc.SetParametersOfInterest(*w.var("s"));
   mc.SetObservables(*w.var("nobs"));
   mc.SetNuisanceParameters(*w.var("b"));

   // these are needed for the hypothesis tests
   mc.SetSnapshot(*w.var("s"));
   mc.SetGlobalObservables(*w.var("b0"));

   mc.Print();
   // import model in the workspace 
   w.import(mc);

   // make data set with the namber of observed events
   RooDataSet data("data","", *w.var("nobs"));
   w.var("nobs")->setVal(nobs);
 

  data.add(*w.var("nobs") );
   // import data set in workspace and save it in a file
   w.import(data);

   w.Print();

   TString fileName = "CountingModel.root"; 

   // write workspace in the file (recreate file if already existing)
   w.writeToFile(fileName, true);

}

I give the smaller uncertainty since I want to match the result of Feldman-Cousins paper

Then
I use the command below:

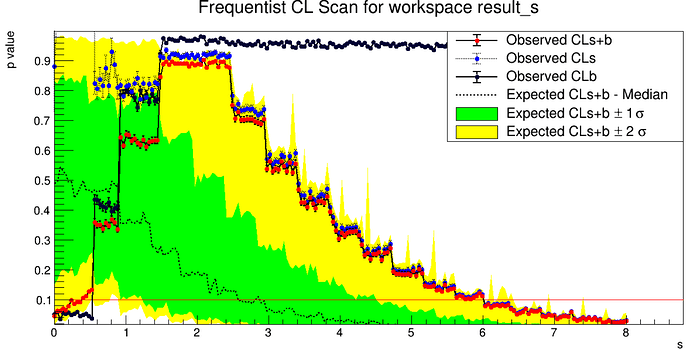
StandardHypoTestInvDemo("CountingModel.root", "w", "ModelConfig"," " , "data", 0, 2, false, 200, 0, 8, 2000, true)

The output is below:

The computed lower limit is: 0.385632 +/- 0.0317312
The computed upper limit is: 6.00396 +/- 0.104173
Expected upper limits, using the B (alternate) model : 
 expected limit (median) 2.57069
 expected limit (-1 sig) 1.23237
 expected limit (+1 sig) 4.5014
 expected limit (-2 sig) 0.146673
 expected limit (+2 sig) 6.02079

does it mean the interval is [ 0.38, 6.00] ?

the plot is

[huyuxiang]

Hi
if the interval is [0.38,6.00] but the FC paper gives the result [0.10, 6.42] when obs = 3, n_bkg =1. I can’t understand the difference.

[huyuxiang]

Hi @moneta ， Could you give some comments on this problems? Thanks !

[moneta]

Hi,

Apologies for the late reply. A small difference between the two is expected, also by giving a systematic uncertainty, although with a small uncertaintie, it smooths the discontinuities in the test statistics (likelihood ratio) given by the discrete data. This is probably the cause of the observed difference.

Lorenzo