Hi Stephan,
Thanks for replying.
With RooAbsPdf::createNLL(), e.g. like this:
Yes, I got that after making the original post.
Could you explain why you want to convolute?
Yes. Basically it’s similar to the reason as in Manipulate the likelihood.
I am fitting for Nsig and I have some additional systematics I want to include that would have the effect of broadening the profile curve of Nsig, giving me larger asymmetric errors than without the systematics included. I have tried the method in that prior post but for me it only works some of the time. Some of the time it fails. So I want to know if there’s a direct way to do it without introducing a new nuisance parameter, e.g. bu directly manipulating the input NLL by adding information about the systematics to it.
Now, your theoryUnc can vary around 1 with a 1-sigma uncertainty of 10%. The trick is that the parameter shows up both in the “plain” likelihood as well as in the constraint term. If it only shows up in the former, it’s an unconstrained uncertainty. If it doesn’t show up at all (or if you set it constant), the systematic is switched off.
Please correct me if I’m wrong but wouldn’t this have the effect of narrowing the profile LL instead of broadening it. What you suggest is what I originally thought but my goal isn’t to “constrain” my parameter of interest Nsig1, which would make the errors smaller. I want the opposite effect after including the systematics. I want to smear the profile LL including the systematics on the profiled parameter (Nsig) into the likelihood function.
So I want to convolve the original likelihood of my parameter of interest L1(Nsig | mu, sigma1) with a Gaussian centered at zero L2(Nsig | 0, sigma2) where sigma2 are is the systematic associated with Nsig thus giving a widened profile curve than the original.
After making this post I tried doing it manually a couple of ways, for example taking the sum of the NLL instead of convolving the LL.
nll = model.createNLL(data, ROOT.RooFit.Extended()) # -Log(L1)
nll2 = TF1("fconstraint2","-TMath::Log(TMath::Gaus(x,[0],[1],0))", NsigLO, NsigHI)
nll2_bind = ROOT.RooFit.bindFunction(nll2, nsig)
total_nll = ROOT.RooAddition("total_nll", "total_nll", ROOT.RooArgList(nll, nll2_bind))
Then create the profile from total_nll.
But I don’t think this is exactly right. Any suggestions you could give on this problem would be greatly appreciated.
Just a quick update. I tried the following method, going off my idea above:
# manually create the NLL from a Gaussian defined by absolute uncertainties
syst_nll = TF1("syst_nll","-TMath::Log(TMath::Gaus(x,[0],[1],0))", sigLO, sigHI)
syst_nll.SetParameters(0, syst_uncert) # parameterize the NLL for the systematics here
# make TF1 a RooAbsReal
syst_NLL_bind = ROOT.RooFit.bindFunction(syst_nll, nsig)
# create NLL from original (unconvolved) fit
nll = model.createNLL(data, ROOT.RooFit.Extended())
# make original NLL a TF1 then a RooAbsReal
nll_asTF = nll.asTF(ROOT.RooArgList(nsig))
nll_rooabsreal = ROOT.RooFit.bindFunction(nll_asTF, nsig)
# get original ("unconvolved") profile for comparison
pll = nll_rooabsreal.createProfile(nsig)
# add them together ("convolution")
total_nll = ROOT.RooAddition("total_nll", "total_nll", ROOT.RooArgList(nll_rooabsreal, syst_NLL_bind))
# minimuzation and other stuff
minimize_total_nll = ROOT.RooMinimizer(total_nll)
minimize_total_nll.minimize("Minuit", "Migrad")
minimize_total_nll.hesse()
minimize_total_nll.minos(nsig)
total_pll = total_nll.createProfile(nsig)
# plot (problem? profiles seem exactly the same even though fit results are not)
frame = nsig.frame()
c1 = ROOT.TCanvas("myCanvas", "myCanvas", 1280*2, 1024*2)
ROOT.gPad.SetLeftMargin(0.15)
total_pll.plotOn(frame, ROOT.RooFit.LineColor(ROOT.kRed))
frame.Draw()
pll.plotOn(frame, ROOT.RooFit.LineColor(ROOT.kBlue))
frame.Draw("SAME")
c1.SaveAs("test.png")
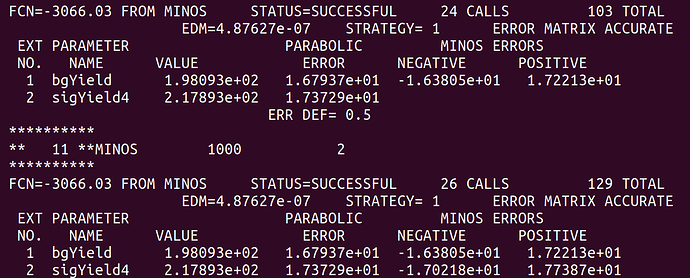
Here is the fit result from before the “convolution”.
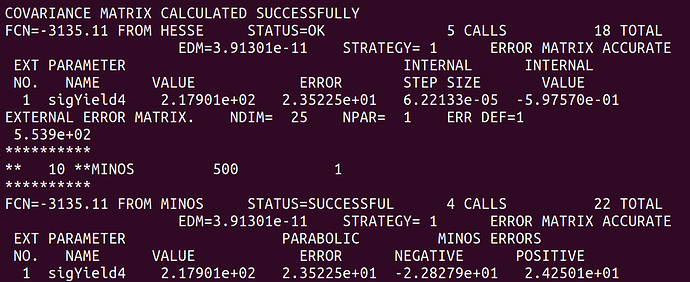
And here is the result after the convolution.
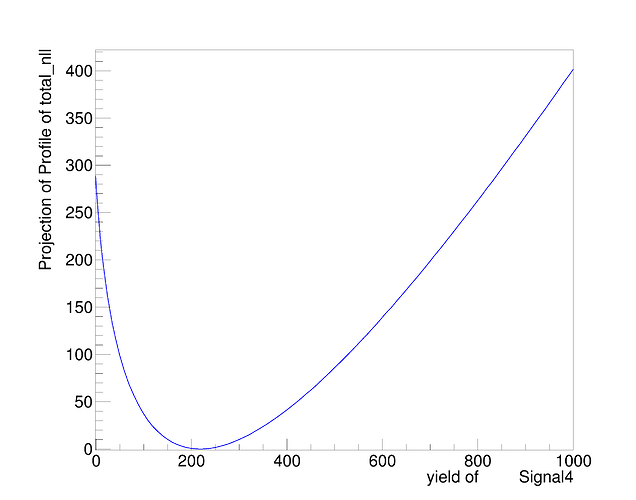
At least naively it does what I expect. The MINOS errors after the convolution are enlarged due to the addition of the systematics. However, this is only a small scale test and when I try to plot the profile on the same canvas they overlap exactly. See the following plot.
There should be red curve for before convolution and blue for after convolution but they overlap so it isn’t apparent is there is a difference. I’m not sure if this is due to a plotting error or I’m not actually getting the result I want as shown in the fit screen captures above.