Dear experts,
I am trying to develop an application with Minuit2 to perform a fit and studies of systematics impact. I am following the Minuit2 guide:
https://root.cern.ch/root/htmldoc/guides/minuit2/Minuit2.html
(especially useful has been the “complete example” in sectioon 7 to start) and the suggestions from the reference manual:
I implemented my own log-likelihood to be minimize, built from Monte Carlo signal and background tempates and simulated data.
The problem I am facing shows when I have large bin contents (of the order of 10^15, which reflects the actual real case), see OUTPUT-1 below. Sometimes this does not happen, and the fit converges, even if with a “large” edm (this of course if I set a high tolerance), see OUTPUT-2 below.
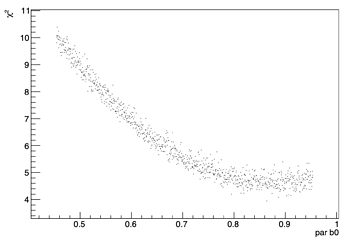
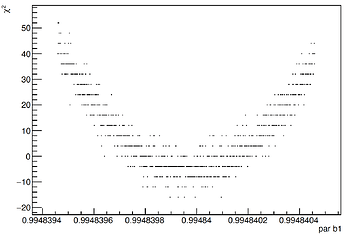
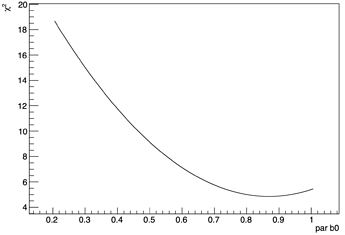
If I perform a scan of the log-lokelihood in this scenario, I see oscillation in the values and the minimum shifted w.r.t. the value found by the minimization:
Also the application of Hesse and Minos fails for such large statistics.
In case of lower bin content (order of 10^4) this is not happening anymore, and the fit seems to converge pretty well with a very low edm: see OUTPUT-3. Also, the likelihood profile in this case is very smooth and centered at the fitted minimum.
The outputs I reported are obtained with low number of paramters (2 bins histograms), but this behaviour of course shows up also in a more realistic case with about 40 parameters.
I was wandering what the problem might be. I have thought this behaviour might be related to numerical problems when dealing with very high statistics (the likelihood is very steep in such a case), but I am not sure and I don’t know how to get to a viable solution. Any help and suggestion is very much appreciated.
Thanks.
OUTPUT-1:
these are the true values for the parameters of interest (b) and nuisance parameters (c):
b0 = 0.7342
b1 = 0.99484
c0 = 0.91775
c1 = 0.65241
c2 = 1.01901
c3 = 0.8635
MnSeedGenerator: for initial parameters FCN = 1.637810634044e+14
MnSeedGenerator: Initial state: - FCN = 1.637810634044e+14 Edm = 3.76327e+14 NCalls = 25
VariableMetric: start iterating until Edm is < 0.002
VariableMetric: Initial state - FCN = 1.637810634044e+14 Edm = 3.76327e+14 NCalls = 25
VariableMetric: Iteration # 0 - FCN = 1.637810634044e+14 Edm = 3.76327e+14 NCalls = 25
VariableMetric: Iteration # 1 - FCN = 6406182107628 Edm = 7.80296e+12 NCalls = 51
VariableMetric: Iteration # 2 - FCN = 3111167594.954 Edm = 3.62633e+09 NCalls = 77
VariableMetric: Iteration # 3 - FCN = 2296913.142666 Edm = 2.45767e+06 NCalls = 91
VariableMetric: Iteration # 4 - FCN = 574.7596185938 Edm = 628.122 NCalls = 105
VariableMetric: Iteration # 5 - FCN = 5.127487952521 Edm = 0.099702 NCalls = 119
Info: VariableMetricBuilder: no improvement in line search
VariableMetric: Iteration # 6 - FCN = 5.127487952521 Edm = 0.099702 NCalls = 120
Info: VariableMetricBuilder: iterations finish without convergence.
Info in VariableMetricBuilder : edm = 0.117619
Info in requested : edmval = 0.002
VariableMetric: After Hessian - FCN = 5.127487952521 Edm = 9.46032e+07 NCalls = 172
VariableMetric: Iteration # 7 - FCN = 5.127487952521 Edm = 9.46032e+07 NCalls = 172
Info: VariableMetricBuilder: Tolerance is not sufficient, continue the minimization
Info in Current Edm is : edm = 9.46032e+07
Info in Required Edm is : edmval = 0.002
Info: VariableMetricBuilder: no improvement in line search
VariableMetric: Iteration # 8 - FCN = 5.127487952521 Edm = 9.46032e+07 NCalls = 183
Info: VariableMetricBuilder: iterations finish without convergence.
Info in VariableMetricBuilder : edm = 9.46032e+07
Info in requested : edmval = 0.002
Info: VariableMetricBuilder: FunctionMinimum is invalid after second try
============= OUTPUT FROM MIGRAD STEP ==============
WARNING: Minuit did not converge.
# of function calls: 172
minimum function Value: 5.127487952521
minimum edm: 94603157.51513
minimum internal state vector: LAVector parameters:
-1.033575118145
-0.9636756223779
-0.9362350803619
-1.051166285965
-0.9099004968978
-0.9463983612187
minimum internal covariance matrix: LASymMatrix parameters:
1.9248376e-13 7.3153301e-16 -3.1274115e-14 -2.8368372e-14 -1.0335189e-14 -6.4726005e-14
7.3153301e-16 1.4479222e-13 -6.8879578e-14 -5.5447371e-15 -4.2384921e-14 -9.5724264e-14
-3.1274115e-14 -6.8879578e-14 3.7869403e-14 7.1912008e-15 2.1789236e-14 5.5859239e-14
-2.8368372e-14 -5.5447371e-15 7.1912008e-15 5.3120358e-15 3.1133086e-15 1.3124619e-14
-1.0335189e-14 -4.2384921e-14 2.1789236e-14 3.1133086e-15 1.3099885e-14 3.1399308e-14
-6.4726005e-14 -9.5724264e-14 5.5859239e-14 1.3124619e-14 3.1399308e-14 8.5117062e-14
# ext. || Name || type || Value || Error +/-
0 || b0 || limited || 0.7043297765156 ||1.122601001047e-06
1 || b1 || limited || 0.893529636327 ||1.085430767767e-06
2 || c0 || limited || 0.9733406113731 ||5.768198255152e-07
3 || c1 || limited || 0.6599852717614 ||1.809553379362e-07
4 || c2 || limited || 1.052786669122 ||3.512754729318e-07
5 || c3 || limited || 0.9434238939071 ||8.527932762736e-07
WARNING: FunctionMinimum is invalid:
Edm is above max
OUTPUT-2:
these are the true values for the parameters of interest (b) and nuisance parameters (c):
b0 = 0.7342
b1 = 0.99484
c0 = 0.91775
c1 = 0.65241
c2 = 1.01901
c3 = 0.8635
MnSeedGenerator: for initial parameters FCN = 1.63781015453e+14
MnSeedGenerator: Initial state: - FCN = 1.63781015453e+14 Edm = 3.76327e+14 NCalls = 25
VariableMetric: start iterating until Edm is < 0.002
VariableMetric: Initial state - FCN = 1.63781015453e+14 Edm = 3.76327e+14 NCalls = 25
VariableMetric: Iteration # 0 - FCN = 1.63781015453e+14 Edm = 3.76327e+14 NCalls = 25
VariableMetric: Iteration # 1 - FCN = 6406181833171 Edm = 7.80296e+12 NCalls = 51
VariableMetric: Iteration # 2 - FCN = 3111159670.394 Edm = 3.62632e+09 NCalls = 77
VariableMetric: Iteration # 3 - FCN = 2296917.36799 Edm = 2.45767e+06 NCalls = 91
VariableMetric: Iteration # 4 - FCN = 574.9675030975 Edm = 628.276 NCalls = 105
VariableMetric: Iteration # 5 - FCN = 5.899223758148 Edm = 0.103659 NCalls = 119
VariableMetric: Iteration # 6 - FCN = 5.800814381795 Edm = 0.000178522 NCalls = 132
============= OUTPUT FROM MIGRAD STEP ==============
Minuit did successfully converge.
# of function calls: 132
minimum function Value: 5.800814381795
minimum edm: 0.0001785223978562
minimum internal state vector: LAVector parameters:
-1.033575103792
-0.9636756070173
-0.9362350546988
-1.051166293802
-0.9099005000428
-0.9463983721168
minimum internal covariance matrix: LASymMatrix parameters:
9.5239342e-16 -1.0221237e-16 -5.3705612e-17 -4.1356337e-17 -2.3913594e-17 -9.4824832e-17
-1.0221237e-16 2.1532393e-16 -3.2889165e-17 -2.0814827e-18 -1.9227531e-17 -4.753091e-17
-5.3705612e-17 -3.2889165e-17 1.2385391e-16 3.8123092e-20 -6.2895675e-18 -1.5166393e-17
-4.1356337e-17 -2.0814827e-18 3.8123092e-20 9.1763512e-16 4.2930372e-18 -1.1601514e-17
-2.3913594e-17 -1.9227531e-17 -6.2895675e-18 4.2930372e-18 1.5459706e-16 -5.7316678e-18
-9.4824832e-17 -4.753091e-17 -1.5166393e-17 -1.1601514e-17 -5.7316678e-18 3.6592898e-16
# ext. || Name || type || Value || Error +/-
0 || b0 || limited || 0.7043298132406 ||7.896535342278e-08
1 || b1 || limited || 0.8935296801434 ||4.185773033738e-08
2 || c0 || limited || 0.9733406874418 ||3.29876087557e-08
3 || c1 || limited || 0.6599852523035 ||7.521005568334e-08
4 || c2 || limited || 1.052786659469 ||3.816055604844e-08
5 || c3 || limited || 0.9434238620516 ||5.591571095032e-08
OUTPUT-3
these are the true values for the parameters of interest (b) and nuisance parameters (c):
b0 = 0.7342
b1 = 0.99484
c0 = 0.91775
c1 = 0.65241
c2 = 1.01901
c3 = 0.8635
MnSeedGenerator: for initial parameters FCN = 1682.211823762
MnSeedGenerator: Initial state: - FCN = 1682.211823762 Edm = 3822.07 NCalls = 25
VariableMetric: start iterating until Edm is < 0.002
VariableMetric: Initial state - FCN = 1682.211823762 Edm = 3822.07 NCalls = 25
VariableMetric: Iteration # 0 - FCN = 1682.211823762 Edm = 3822.07 NCalls = 25
VariableMetric: Iteration # 1 - FCN = 69.03242531743 Edm = 75.9613 NCalls = 39
VariableMetric: Iteration # 2 - FCN = 5.481917023955 Edm = 0.0527581 NCalls = 53
VariableMetric: Iteration # 3 - FCN = 5.418503885897 Edm = 0.0201209 NCalls = 67
VariableMetric: Iteration # 4 - FCN = 4.700495966253 Edm = 0.104642 NCalls = 84
VariableMetric: Iteration # 5 - FCN = 4.558448766166 Edm = 0.0017108 NCalls = 98
VariableMetric: Iteration # 6 - FCN = 4.556029051722 Edm = 0.000684201 NCalls = 112
VariableMetric: After Hessian - FCN = 4.556029051722 Edm = 0.0823377 NCalls = 152
VariableMetric: Iteration # 7 - FCN = 4.556029051722 Edm = 0.0823377 NCalls = 152
Info: VariableMetricBuilder: Tolerance is not sufficient, continue the minimization
Info in Current Edm is : edm = 0.0823377
Info in Required Edm is : edmval = 0.002
VariableMetric: Iteration # 8 - FCN = 4.476097792467 Edm = 0.00246463 NCalls = 165
VariableMetric: Iteration # 9 - FCN = 4.473988356004 Edm = 5.727e-05 NCalls = 178
============= OUTPUT FROM MIGRAD STEP ==============
Minuit did successfully converge.
# of function calls: 178
minimum function Value: 4.473988356004
minimum edm: 5.726997259221e-05
minimum internal state vector: LAVector parameters:
-0.9666789115697
-0.9583534822507
-0.9515582959783
-1.059631311471
-0.9199248160373
-0.9736282570089
minimum internal covariance matrix: LASymMatrix parameters:
0.0040357264 -0.00033686465 -0.00057112663 -0.00064862698 -0.0001422839 -0.0013036399
-0.00033686465 0.0024825049 -0.001147331 -4.6292979e-05 -0.00071914945 -0.0015707027
-0.00057112663 -0.001147331 0.00067632323 0.00014074665 0.00037608526 0.0010024361
-0.00064862698 -4.6292979e-05 0.00014074665 0.00020349194 5.284164e-05 0.00027827516
-0.0001422839 -0.00071914945 0.00037608526 5.284164e-05 0.0002387877 0.00054630726
-0.0013036399 -0.0015707027 0.0010024361 0.00027827516 0.00054630726 0.0016115951
# ext. || Name || type || Value || Error +/-
0 || b0 || limited || 0.8849812101511 ||0.1803077984148
1 || b1 || limited || 0.9087692626569 ||0.1431540064686
2 || c0 || limited || 0.9283952438061 ||0.07546345946709
3 || c1 || limited || 0.6391240923498 ||0.03489070236018
4 || c2 || limited || 1.022219650861 ||0.04681071662603
5 || c3 || limited || 0.8653433433502 ||0.1128370321398