Issues with Double Gaussian Function Construction for Different Ranges

[SAYAN_CHATTERJEE]

Dear experts,

I am currently developing a double Gaussian fitting function within the range of [−4.0,4.0]. The design involves two Gaussian components:

1. The first Gaussian contributes to the full range of [−4,4].
2. The second Gaussian is restricted to the ranges [−4,−2] and [2,4]. Both Gaussians have a mean at 0.

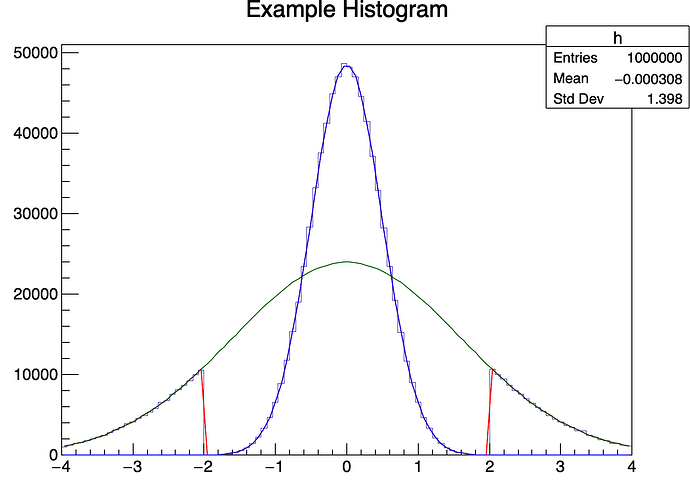
However, I am encountering an issue with a discontinuity at +2 and −2, which was not the intended behavior. The second Gaussian, generated based on the data points from the specified regions, should have an extended contribution in the central peak region [−2,2]. This contribution should not depend on data points from the region [−2,2].

Below is the macro I am working with:

//macro.C

#include <TROOT.h>
#include <TFile.h>
#include <TH1F.h>
#include <TF1.h>
#include <TCanvas.h>

// Define the first function f1 (Gaussian with fixed mean at 0.0, symmetric in [-4, 4])                                                                                               
Double_t f1(Double_t *x, Double_t *par) {
    Double_t arg = (x[0] - 0.0) / par[1];  // Mean fixed at 0.0                                                                                                                       
    return par[0] * exp(-0.5 * arg * arg);  // Gaussian: par[0] = amplitude, par[1] = sigma                                                                                           
}

// Define the second function f2 (only contributes in [-4, -2] and [2, 4], symmetric)                                                                                                 
Double_t f2(Double_t *x, Double_t *par) {
    if ((x[0] >= 2.0 && x[0] <= 4.0) || (x[0] >= -4.0 && x[0] <= -2.0)) {
        Double_t arg = (x[0] - 0.0) / par[1];  // Mean fixed at 0.0                                                                                                                   
        return par[0] * exp(-0.5 * arg * arg);  // Gaussian: par[0] = amplitude, par[1] = sigma                                                                                       
    }
    return 0;  // Outside the range [-4, -2] and [2, 4], f2 = 0                                                                                                                       
}

// Define the combined function F = f1 + f2                                                                                                                                           
Double_t F(Double_t *x, Double_t *par) {
    // par[0]: amplitude of f1, par[1]: sigma of f1                                                                                                                                   
    // par[2]: amplitude of f2, par[3]: sigma of f2                                                                                                                                   
    return f1(x, par) + f2(x, &par[2]);
}

void macro() {
    // Create a histogram or load your data here                                                                                                                                      
    TH1F *h = new TH1F("h", "Example Histogram", 100, -4, 4);
    //h->FillRandom("gaus", 100000);  // Filling with random data for example                                                                                                         

    // Define the combined function F                                                                                                                                                 
    TF1 *fitFunc = new TF1("fitFunc", F, -4, 4, 4);  // 4 parameters: 2 for f1 and 2 for f2 
    fitFunc->SetParameters(1.0, 0.5, 0.5, 1.6);

    for (int i = 0; i < 1000000; i++) {
      double random_number = fitFunc->GetRandom(-4, 4);
      h->Fill(random_number);
    }

// Perform the fit                                                                                                                                                                
    h->Fit("fitFunc", "R");
    h->Fit("fitFunc", "R");
    h->Fit("fitFunc", "R");

    // Draw the result                                                                                                                                                                
    TCanvas *c1 = new TCanvas("c1", "Fitting Example", 800, 600);
    h->Draw();
    fitFunc->Draw("same");

    TF1* f11 = new TF1("f11", f1, -4, 4, 2);
    f11->SetParameter(0, fitFunc->GetParameter(0));
    f11->SetParameter(1, fitFunc->GetParameter(1));
    f11->SetLineColor(kBlue);
    f11->Draw("same");

    TF1* f22 = new TF1("f22", f1, -4, 4, 2);
    f22->SetParameter(0, fitFunc->GetParameter(2));
    f22->SetParameter(1, fitFunc->GetParameter(3));
    f22->SetLineColor(kGreen+3);
    f22->Draw("same");
}

I would kindly request the experts to help constructing the model.

Thanks in Advance.

Sayan

============================================================

[Danilo]

Dear Sayan,

Thanks for the interesting post.

There is something I do not fully understand.
You say:

@SAYAN_CHATTERJEE

should have an extended contribution in the central peak region [−2,2].

But then your second function is

Double_t f2(Double_t *x, Double_t *par) {
    if ((x[0] >= 2.0 && x[0] <= 4.0) || (x[0] >= -4.0 && x[0] <= -2.0)) {
        Double_t arg = (x[0] - 0.0) / par[1];  // Mean fixed at 0.0                                                                                                                   
        return par[0] * exp(-0.5 * arg * arg);  // Gaussian: par[0] = amplitude, par[1] = sigma                                                                                       
    }
    return 0;  // Outside the range [-4, -2] and [2, 4], f2 = 0                                                                                                                       
}

Therefore, as per the if condition, without any contribution in the peak region, by construction, no?

Cheers,
D

[SAYAN_CHATTERJEE]

Dear @Danilo ,

Thanks for your response.

I wanted to generate the 2nd gaussian based on the only data points of [2,4] and [-4,-2]. But this gaussian will be in the full region [-4,4].

Double_t f2(Double_t *x, Double_t *par) {
if ((x[0] >= 2.0 && x[0] <= 4.0) || (x[0] >= -4.0 && x[0] <= -2.0)) {
Double_t arg = (x[0] - 0.0) / par[1]; // Mean fixed at 0.0
return par[0] * exp(-0.5 * arg * arg); // Gaussian: par[0] = amplitude, par[1] = sigma
}
return 0; // Outside the range [-4, -2] and [2, 4], f2 = 0
}

If I open the if condition, then the discontinuity will be off but the gaussian will not be restricted between [-4, -2] and [2, 4].

So, I want to draw the 2nd gaussian in the full range [-4,4], but it’s parameters Sigma and Amplitude should only estimated based on the region of [-4, -2] and [2, 4] data points, and mean must be 0.

Is it clear to you @Danilo now?

Could you please point me out where I am doing wrong? Is there any other way of doing it?

Thanks and regards,
Sayan

[moneta]

HI,

The way you build the funciton will be discontinous at -2 and 2, and therefore will not work correctly. Maybe you could try a different funciton, such as the double side crystal ball function (see Crystal Ball function - Wikipedia and Fit using Double sided crystal ball function )

Lorenzo