Interpolation option for RooHistPdf

Roofit and RooStats
1

Hello, I am trying to model a 2D data set using RooHistPdf with interpolation order = 2
The ROE_Mbc and mu_pBrest are the two dimensions of the PDF model, and con is the modeled RooHistPdf.

RooRealVar ROE_Mbc("ROE_Mbc","ROE_Mbc",5.1,5.3);
RooRealVar mu_pBrest("mu_pBrest","mu_pBrest",2.1,3.5);
Double_t Mbc_Bins[10] = {5.1,5.14,5.18,5.22,5.26,5.27,5.28,5.2897786,5.2897788,5.3};
RooBinning MbcBins(9,Mbc_Bins,"MbcBin");
mu_pBrest.setBins(10);
mu_pBrest.setRange("Mom_box",2.11,3.49);
ROE_Mbc.setBinning(MbcBins);
ROE_Mbc.setRange("Mbc_box",5.11,5.29);
RooDataHist *dh_con = new RooDataHist("dh_con","dh_con",RooArgList(ROE_Mbc,mu_pBrest),data);
RooHistPdf con("conhist","conhist",RooArgList(ROE_Mbc,mu_pBrest),*dh_con,2) ;

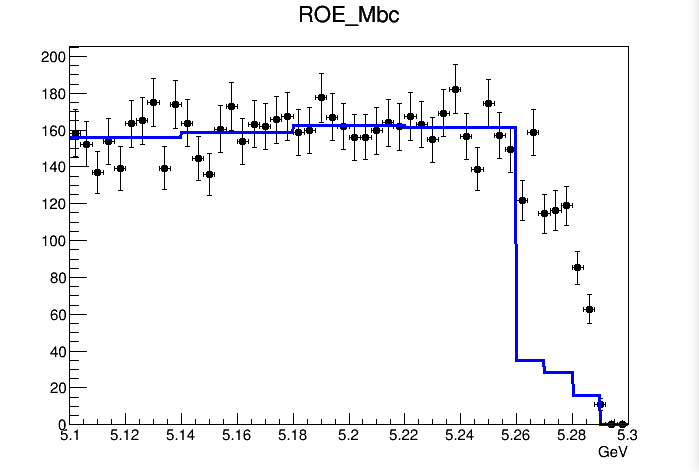
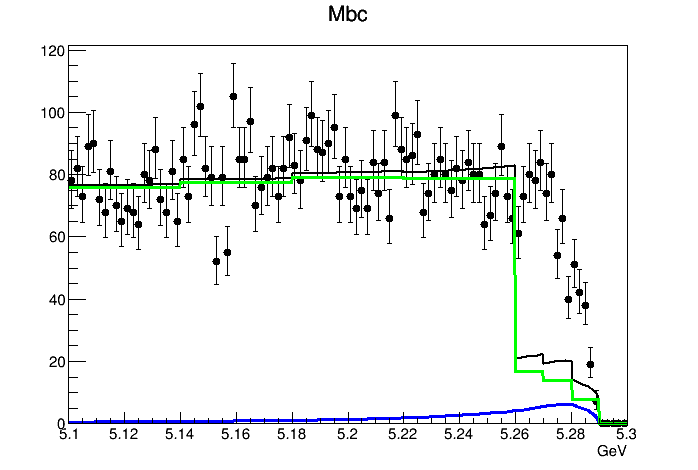
When I try to draw the whole-region 2D PDF, it looks like this

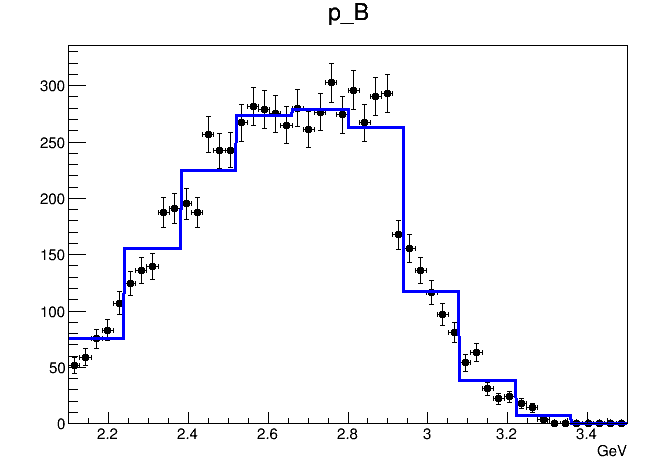
image
image699×472 5.58 KB

image
It seems that the interpolation option is useless. The shape of the PDF is not getting smoother.
However, if I plot the model in ProjectionRange("Mom_box") and ProjectionRange("Mbc_box"), the interpolation works.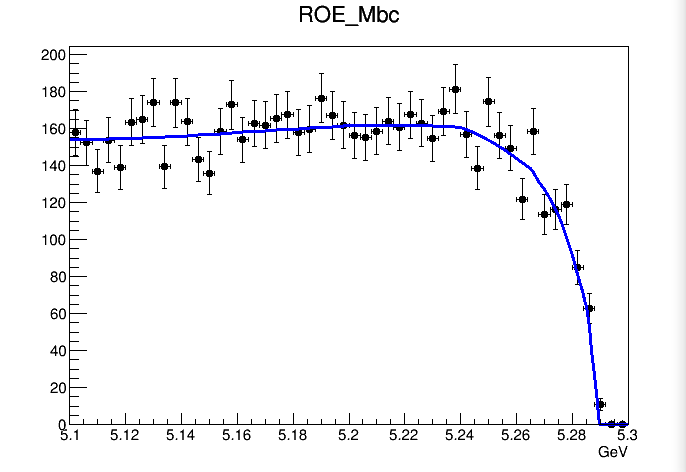
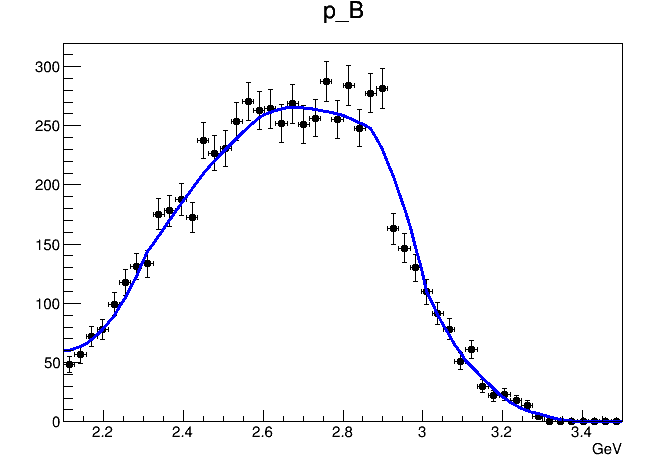
image
image
Is this just some kind of plotting feature or is it just illegal to specify interpolation option in 2D histogram PDF?

There is a second question. For the ROE_Mbc dimension, the bin size is different in each bin. In the whole region plot, there is big drop at ROE_Mbc>5.26. This is because for ROE_Mbc>5.26, the size of the bins is smaller, so there is less number of events. I wonder if there is any possibility to normalize each bin according to there bin size (i.e. Can we have for example PdfValueAtCertainBin = NumberOfEventsInThatBin/SizeOfThatBin?). By the way, I don’t see the big drop occurs in the projection plot. I suspect that for some reason the normalization is done in the projection plot.
fitcon2D.C (1.8 KB)

2

I’m sure @StephanH can help you

3

Hello @andychin912,

  1. When you plot on a frame that has custom bins, the PDF is evaluated in the centre of the bin, and plotted as a histogram. The interpolation happens only when computing the probability in the bin centre. That’s why you get steps.
  2. When you start projecting, the PDF is integrated over the invisible observables. Now, it uses as many points as bins on the frame, but these are connected with smoother lines. You can actually see the changes of the curvature in the last plot.
  3. PDFs are plotted by evaluating them at the bin centre. Data, however, are plotted as counts, so they jump up and down when bins are changing size.
  4. In your case, however, all bin sizes for the data histograms seem to be the same. You probably only need a few more bins to make the step in the 4th plot a bit smoother. Are you plotting dh_con or something else? I would expect less bins on the plot, since you are only using 9 and 10 bins for the dh_con.
4

Hello @StephanH, thanks for the prompt reply.
In these plots I only plot the data and the RooHistPdf con.
After defining the RooHistPdf, I reset the bin size to ROE_Mbc.setBins(50) and mu_pBrest.setBins(50). That’s why the data has more bins than the PDF.
The step in the data of the 4th plot is due to some physics issue but not plotting issues(I might have to investigate it further thought).
What I’m worrying about is the jump of the histogram in the 1st plot at 5.26. Why do we have the jump, and why the same jump does not occur in the 3rd plot?
For convenience, I’ve attached the full script in the original post.

5

I’m sure it’s physics, because it’s in the data. If it’s just by coincidence, a binning artifact, you can use a slightly different number of bins, say between 48 and 52.

I assume that’s because the initial template dh_con from which you create the histPdf “jumps down” at this location. Try to plot dh_con directly with the initial binning, and you should see that. If you can use different bins, it might look better.

When you start projecting out only a part of the full volume, RooFit starts to integrate over the binned distribution. This will make use of the interpolation, and that’s why it looks smoother. You could kind of say that RooFit subdivides bins in this case.

6

The drop in the 1st plot is conspicuous. but in the 3rd plot the drop seems completely disappeared and the data and model matches pretty well. It’s very hard for me to believe that applying the interpolation could make this drop disappear without a trace. Unless plot1 and plot3 have completely different meaning. I wonder whether plot 1 is showing a “PDF” or it’s just showing the number of events in the bin of the template dh_con? If it is showing the number of events in the bin, the drop makes sense because smaller bins should get less events. However, if it is showing a “density function”, then I really cannot understand why there is a drop…

Moreover, I encountered another problem. When I use the con model in an unbinned maximum likelihood fit, am I using the interpolated PDF or the step-like hist pdf? it seems that no matter I’m using projection plot or not, the fitting result shows steps.

image
image698×470 6.22 KB

(the green line is the con model and the blue one is another component in my fit.)

7

It’s probably not the interpolation that makes it disappear. The effect of the interpolation is probably what you see comparing the black curve vs the green.
If you want to see what an unbinned fit would see, plot the PDF as a data-weighted average using ProjWData as shown here:
https://root.cern.ch/doc/master/rf303__conditional_8C.html

This evaluates the PDF at each data point, and uses the results to create a curve. And that’s also what an unbinned fit does.

8

The black curve is not an interpolated version of the green line. It’s just an superposition of the green line and the blue.

9

Ok. But that shouldn’t change the data-weighed average. Did you try that?

10

I did

RooDataSet *data_mom = (RooDataSet *)data->reduce(mu_pBrest);
Model.plotOn(xframe, ProjWData(*data_mom));

The result seems to be OK.
Thanks for your help.

11

That’s good to see!

12

To finish this:
I now know why the distribution comes out binned when projecting:
When the RooHistPdf sees that one whole dimension is integrated out, it speeds up the process by summing over all the bins - no interpolation. This only happens when integrating, but projecting is obviously integrating.
With the data-weighted average, the PDF is projected by evaluating it at the locations of all data points. Now, the interpolation is used again (as for unbinned fits).

13

This topic was automatically closed 14 days after the last reply. New replies are no longer allowed.