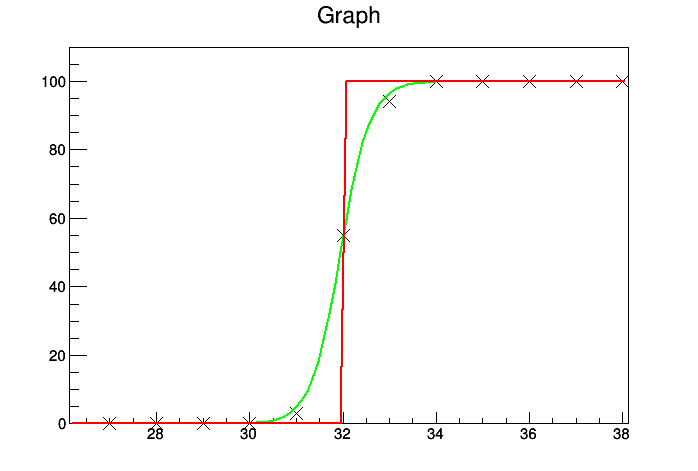
Hi, I have a macro which fits more or less a custom error function/vertically reflected Fermi-Dirac distribution to data point from a threshold scan for all pixels on chip of 1024x512 pixels. In the case of most (99%) of pixels this works fine, with some curves being refit if the detected parameters seems unreasonable (though these tests are hard to perform as these ‘bad fits’ still return IsValid=TRUE), and due to their being thousands of bad fits it is impossible to go through on a case by case basis. However, 1% of pixels still have issues fitting, with the fit gradients being far steeper than true. What is stranger than this, however, is that when I extract these original threshold scan data from my tree and fit using exactly the same function, range, and initial parameters in a separate macro, the fit is perfect, but no matter how many times I try and refit within the original macro I cannot reproduce these correct fits. Example of the issue produced by the second macro, with the original fit parameters shown in red, and the correct fit in green.
Macro for reading data into tree and performing original hits:
AnalyseT2.C (6.6 KB)
Data file for reading which isn’t 1GB (think it should still contain some dubious fits)
row0.txt (1.5 MB)
Fit code used in secondary macro (which produces above figure):
for(int j = 0 ;j<myHit.GetSize(); ++j){
PlotHit->SetPoint(j,100-j,myHit[j]);
}
TCanvas *plotdodge=new TCanvas();
//fit object to show fit from AnalyseT macro
TF1 *f2 = new TF1("f1","100/(1+exp(([0]-x)/[1]))",5,55);
//fit obejct to refit graph
TF1 *f1 = new TF1("f1","100/(1+exp(([0]-x)/[1]))",5,55);
f2->SetParName(0,"Threshold");
f2->SetParName(1,"Response");
f2->SetParameters(*myThresh,0.5);
PlotHit->SetMarkerStyle(5);
PlotHit->SetMarkerSize(2);
//fix f1 to keep old parameters
f1->FixParameter(0,*myThresh);
f1->FixParameter(1,*myResponse);
//plot old and new fits on same canvas
plotdodge->cd();
PlotHit->Draw("AP");
f2->SetLineColor(3);
PlotHit->Fit(f2);
f1->Draw("same");
plotdodge->Update();
Is it likely launching something like this second macro segment from the first would help? At present I am just ignoring results with seemingly bad gradients, but would ideally like to have a complete data set.