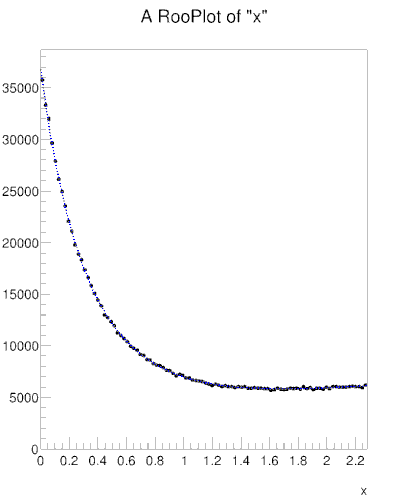
-
the Pdf is user defined functions;
-
the Data is defined by model.generate();
my code is
#ifndef __CINT__
#include "RooGlobalFunc.h"
#endif
#include "RooRealVar.h"
#include "RooDataSet.h"
#include "RooGaussian.h"
#include "RooChebychev.h"
#include "RooAddPdf.h"
#include "TCanvas.h"
#include "TAxis.h"
#include "RooPlot.h"
#include <vector>
#include "RooGenericPdf.h"
using namespace std;
using namespace RooFit ;
void simple(){
RooRealVar x("x","x",0,2.2794) ;
RooRealVar kappa("kappa","kappa",2.2794,2.27,2.29);
RooGenericPdf model("model","model","0.665/(8*TMath::Pi()/3)/(kappa*kappa*pow((1+x),3))*(kappa*(1+pow((1+x),2))-4*x/kappa*(1+x)*(kappa-x))",RooArgSet(x,kappa));
RooDataSet* data = model.generate(x,1E6);
model.fitTo(*data);
RooPlot* xframe = x.frame();
data->plotOn(xframe);
model.plotOn(xframe,LineStyle(kDashed));
TCanvas *c = new TCanvas("c","c",800,1000);
xframe->GetXaxis()->SetTitleOffset(1.5);
xframe->Draw();
}
And the fit result is here:
Processing simple.cxx…
RooFit v3.60 – Developed by Wouter Verkerke and David Kirkby
Copyright © 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:NumericIntegration – RooRealIntegral::init(model_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:NumericIntegration – RooRealIntegral::init(model_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:NumericIntegration – RooRealIntegral::init(model_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minization – RooMinimizer::optimizeConst: activating const optimization
** 1 **SET PRINT 1
** 2 **SET NOGRAD
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 kappa 2.27940e+00 2.00000e-03 2.27000e+00 2.29000e+00
** 3 **SET ERR 0.5
** 4 **SET PRINT 1
** 5 **SET STR 1
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
** 6 **MIGRAD 500 1
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=641583 FROM MIGRAD STATUS=INITIATE 4 CALLS 5 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 kappa 2.27940e+00 2.00000e-03 2.01742e-01 -4.95878e-01
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=641583 FROM MIGRAD STATUS=CONVERGED 14 CALLS 15 TOTAL
EDM=4.99876e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 kappa 2.28091e+00 5.23373e-03 3.05704e-01 4.04022e-03
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 1 ERR DEF=0.5
3.037e-05
** 7 **SET ERR 0.5
** 8 **SET PRINT 1
** 9 **HESSE 500
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=641583 FROM HESSE STATUS=OK 5 CALLS 20 TOTAL
EDM=4.90868e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 kappa 2.28091e+00 5.16186e-03 1.22282e-02 9.14439e-02
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 1 ERR DEF=0.5
2.945e-05
The fit error is at the level of 1e-3(now the entries is 1E6);
Is it possible to improve the level of error(such as:1e-4) when the entries is still as 1E6?
That is, how I improve my fit error without changing the entries?