How to correctly extract the chi2, ndf, p-value of a RooFitResult

[astauffe]

Hi everybody,

I currently have a question regarding the integral of a model component pdf that I posted here (https://root-forum.cern.ch/t/roofit-integral-error-and-manual-question/45864), where I am receiving great help from @jonas. I also have another issue regarding the same model but thought it would make sense to open a separate topic. However it concerns the same simple model that I posted in the original question and also my question is very general I think. My questions is about the “goodness of fit” measure after fitting the model (in the previous topic). Explicitly, how to extract it. I’ve found a couple of ways, but not all of them give me the same result or a reasonable result at all. Maybe someone can clarify this for me? Probably I am doing something stupid…
I will try to first provide the context of my problem and then the methods I tried and the results I have so far. So, what I am doing is fitting the model to a histogram as

RooFitResult *fit_result_data = model.fitTo(hdata, Range("fullRange"), Save(), PrintLevel(-1));

I can also plot it without trouble:

RooPlot *xframe04 = x.frame(Title("RooFit fit"));
hdata.plotOn(xframe04, Name("Data"));
model.plotOn(xframe04, Name("Model with errors"), VisualizeError(*fit_result_data));

and so on… Now, I would like to extract a measure for the goodness of fit. Preferably the chi², ndf, chi²/ndf and the corresponding p-value to test the hypothesis of the histogram following the distribution/pdf-model. In general I understand that the ndf should be “50 - 2 - m”, as I have 50 bins, 2 fitting parameters (A_sig and A_bkg, see model of previous topic) and some number “m” of bins with 0 entries (I have two unweighted histograms).

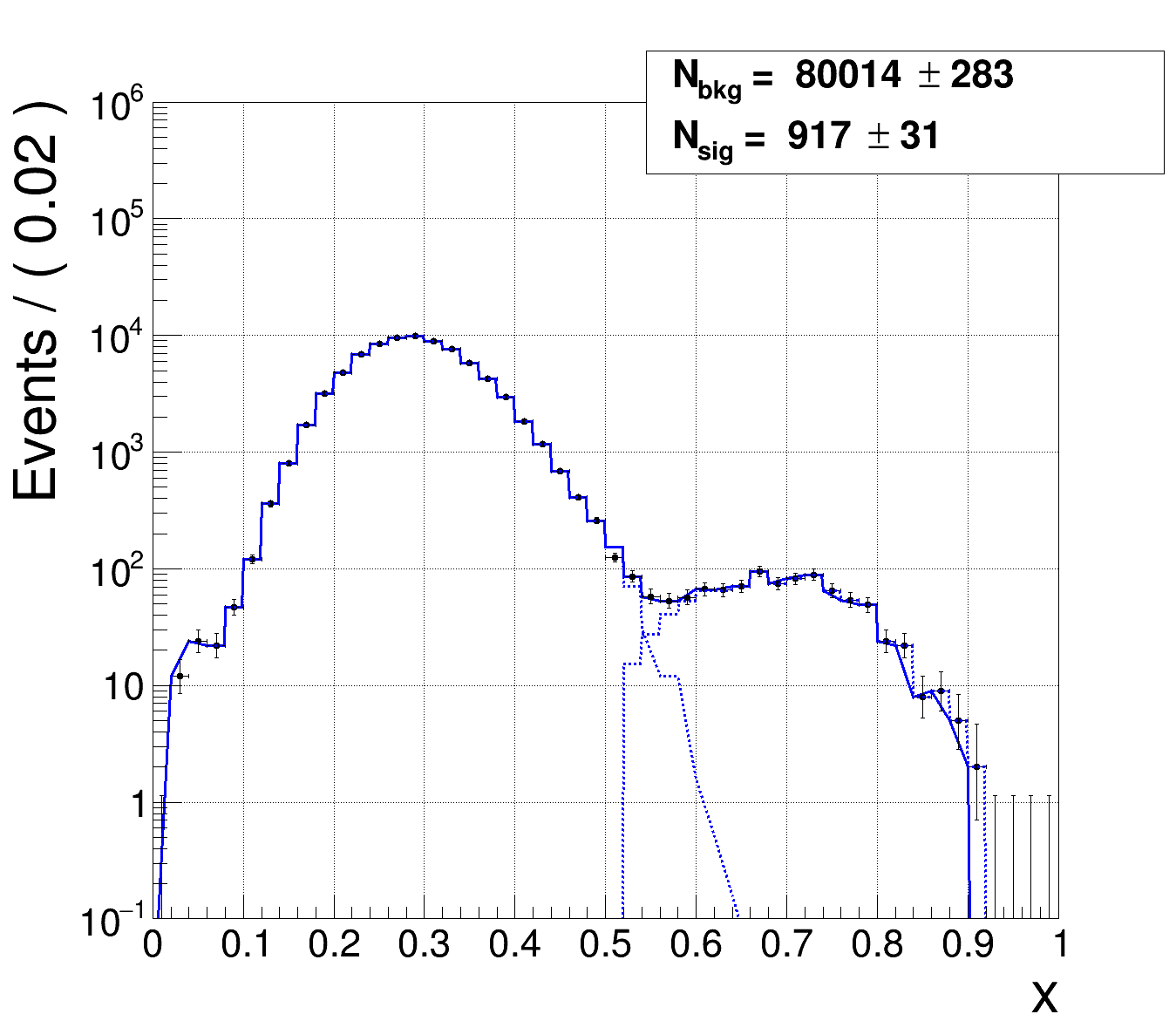
I would like to illustrate to cases; one very good fit (case 1) and one “ok”-fit (case 2).

Case 1:
m = 5, so 5 bins with 0 entries. Very good fit, basically fitting the model to the data I extracted it from. So, I know that the chi² should be very small and the ndf should be 50 - 2 - 5 = 43.

(blue is the whole model and the dashed lines are the two components, black is the data)

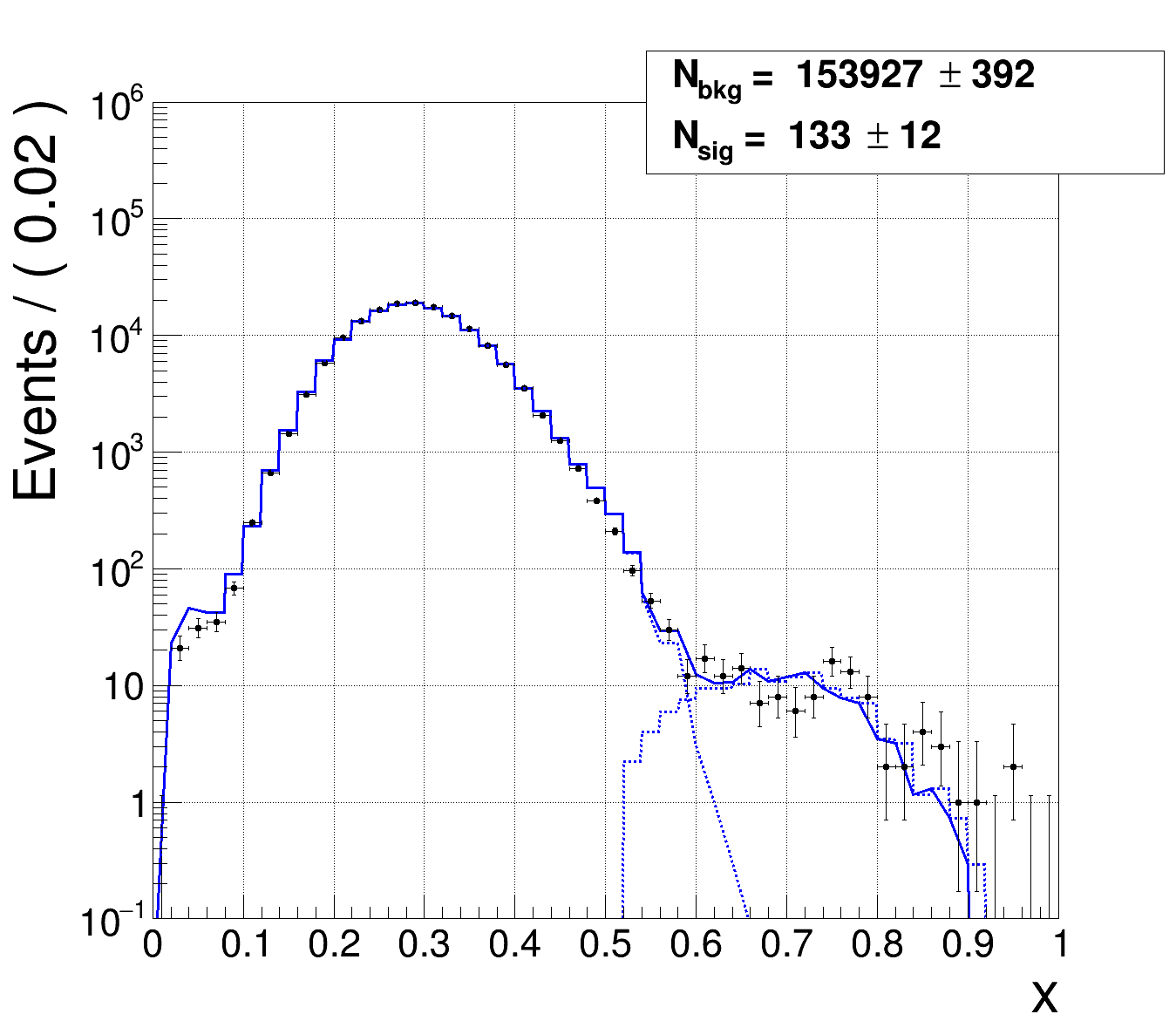
Case 2:
m = 4, so 4 bins with 0 entries. Ok fit, basically fitting the model to independent data and testing whether the data agrees with the model. I only know that the ndf should be 50 - 2 - 4 = 44 and the chi² could be anything.

Now I will just summarize my attempts to extract the chi2, ndf and p-value so far and the results/issues I have.

Method 1 - RooPlot::chiSquare():
My first idea was to apply this method right after plotting as

cout << "chi^2/ndf = " << xframe04->chiSquare(2) << endl;

where 2 indicates the nr. of fitting parameters… this returns me:
case 1: chi^2/ndf = 0.465877
case 2: chi^2/ndf = 4.91932
This alone would be believable. I think there is no similar method to also directly evaluate the chi² or the p value? However, since I know the ndf for each case, I can calculate the chi² by hand and with ROOT::Math::chisquared_cdf_c(chi², ndf) am able to get the p value directly. Then, I end up with
case 1: chi^2/ndf = 0.465877, chi^2 = 20.0327, ndf = 43, p-value = 0.998919 (amazing as expected)
case 2: chi^2/ndf = 4.91932, chi^2 = 226.289, ndf = 44, p-value = 2.33382e-26 (ok very bad…)
It is unclear to me however, how one could supply a range here?

Method 2:
Another possibility seems to be to use “createChi2” directly on the model as:

RooAbsReal * chi2_o_ndf = model.createChi2(hdata, Range("fullRange"));
cout << "chi2_o_ndf: " << chi2_o_ndf->getVal() << endl;

It seems to me, that the advantage here is that one can supply a range very easily. The number of parameters can not be supplied I think, but they are probably taken from the model directly. This results in:
case 1: chi^2/ndf = 5.45976, p-value = 3.05669e-28
case 2: chi^2/ndf = 3.10989e+12, p-value = 0
where I used again the same steps as in method 1 to get to the p-value. These values are completely different…

Method 3:
Another idea was to turn the model into a histogram (either via “createHistogram” or via “asTF” and then “GetHistogram”) and then calculate the chi² via TH1::Chi2Test" as:

TH1 * th_model = model.createHistogram("chi_histo", x, IntrinsicBinning(), Extended(kTRUE));
// or similar, and then:
th_model->Chi2Test(hdata, "UU P");

this prints the directly the whole result of a chi2 test of two unweighted histograms. Here it is unclear to me, how one could set the number of parameters though (or a range). The results are:
case 1: Chi2 = 5.372482, Prob = 1, NDF = 44, igood = 0
case 2: Chi2 = 292.846044, Prob = 4.58335e-38, NDF = 45, igood = 1
which, in my opinion, is problematic in many ways. In case 1, the chi2 is similar to method 2 but not equal. The ndf is 44 instead of 43 (I guess it just assumes that the number of parameters is 1 and ignores all bins with 0 entries automatically). And then igood = 0 should suggest that both histograms have no bins with 0 entries, but the ndf suggests otherwise (and I know, that it is otherwise). In case 2 the chi2 is neither similar to method 1 nor to method 2…

Method 4:
Intuitively, my first idea was that one should be able to somehow extract the chi2, ndf, pvalue from the initial RooFitResult. But this does not seem to be possible as far as I learned.
Or I thought maybe one can transform it into a traditional TFitResult and then use “->Ndf()”, “->Chi2” and “->Prob()”. But I think this is also not possible. So, method 4 has no results.

Sorry for this super long question, but at this point I am really confused as to which method I should use and why they don’t coincide. What am I doing wrong? Please help me

Best,
Alex

[astauffe]

Hi everybody,
is it possible to still answer this question? Basically, my question was: “What is the correct way to extract a chi², ndf and p-value of of a RooFitResult?”. Of secondary importance is: “Why do all my tried methods lead to different results?”. I am sorry if I provided too much or little detail or asked my question in the wrong way. Also I am using Root v6.24/02 and if necessary I could come up with a minimal working example.
Best,
Alex

[jonas]

Hi @astauffe,

sorry for the late reply! It was not an easy question and it took me quite some time to wrap my head around it. I’ll comment on all of the 4 methods you propose and then conclude with a recommendation.

First of all: keep in mind that the chi2 test is an approximation in your case. Indeed, the chi2/ndf follows a chi2 distribution if the residuals are Gaussian, but we are talking here about histograms with Poisson errors with not so many events per bin (for large x in your plot). So the Gaussian approximation is not perfect, and hence your chi2/ndf will only be approximately distributed according to a chi2 distribution. Just a thing to keep in mind when you interpret your results.

Method 1 - Using RooCurve::ChiSquare()

As you say the results look correct, but there is one caveat. You have a continuous model pdf (if I remember correctly, at least with a Gaussian for the background right?), and when you make the plot you have no control over how many points are sampled to make the plot. For the continuous pdf with non-vanishing second derivative, the prediction for each bin is the integral over each bin times the number of predicted events from the extended term. I don’t know exactly how you made that plot you are showing, but it seems like the continuity is lost. The RooCurve::chiSquare() function tries to estimate the integral based on the points sampled for the curve, which might be or might not be what you want (maybe your pdf is a binned pdf anyway, then it’s okay).

Method 2 - Using RooAbsPdf::createChi2()

I think this is in the best way, but you interpreted the results wrong and also have to be careful with the parameters you pass to the createChi2 function.

First, it doesn’t divide by ndf, i.e. the number of non-zero bins minus the number of parameters. You have to do this manually afterwards, which is what you did, right? And now you are surprised why the numbers are still much larger than for method 1?

I think the problem here is how you define the uncertainty in the denominator of the chi2. By default for a Poissonian dataset, the method takes the square root of the pdf value in the bin center as the uncertainty. This is very wrong for very small predictions like you have near x = 1. Take a look at the 3rd-to last bin in the “bad” fit, I think this is what happens: your model predicts a very small value, resulting in a extremely small and wrong uncertainty prediction. However, you observe 2 events, and the residuum divided by the error makes the chi2 blow up.

Can you try changing the error definition to Poissonian confidence intervals from the data? This is what RooCurve::chiSquare() does by the way, and you can get the same uncertainty definition in createChi2 like this:

model.createChi2(hdata, Range("fullRange"),
                 Extended(true), DataError(RooAbsData::Poisson));

Note that I also added the Extended(true) command such that the prediction of the total number of events is taken from the extended pdf and not from the data. If you divide what is printed by ndf, you should get the correct result.

Still, this method doesn’t get it right if you pdf is continuous, because it just takes the pdf value in the bin center. If this is a problem for you, you can consider wrapping the pdf in a RooBinSamplingPdf, which turns the continuous pdf into a binned pdf where the values for each bin are obtained by integration.

Method 3 - Export to TH1 and use TH1::Chi2Test()

That’s an interesting approach and the results look fine, but I don’t think it’s correct. As you can see in the function documentation, the Chi2Test function is meant to compare two histograms that are both the result of a statistical process: either unweighted data or weighted Monte Carlo simulation. Your case is different, because you have a model from your fit that has no uncorrelated statistical error for each bin, like the TH1::Chi2Test assumes for both histograms.

So the values you obtain with this method seemingly look fine but are probably wrong because the test assumes that your model predictions are not the actual predictions but the result of MC from simulation around which the true predictions fluctuate. Plus you also have the binning effects mentioned before.

Method 4 - Trying to use the RooFitResult

Exactly, it’s not possible to get chi2, ndf, and pvalue of the chi2 for a RooFitResult. Fitting is separate from hypothesis testing, and the chi2 test is a form of hypothesis testing.

In conclusion, your method 2 is the recommended one, you just have to set the correct command arguments. And consider wrapping your model in a RooBinSampling pdf if it is continuous, to avoid binning effects.

Thanks for your patience and let me know if the recommendation worked for you or if you have further questions!

Cheers,
Jonas

[calvin56]

@jonas

Hi @astauffe,

sorry for the late reply! It was not an easy question and it took me quite some time to wrap my head around it. I’ll comment on all of the 4 methods you propose and then conclude with a recommendation.

First of all: keep in mind that the chi2 test is an approximation in your case. Indeed, the chi2/ndf follows a chi2 distribution if the residuals are Gaussian, but we are talking here about histograms with Poisson errors with not so many events per bin (for large x in your plot). So the Gaussian approximation is not perfect, and hence your chi2/ndf will only be approximately distributed according to a chi2 distribution. Just a thing to keep in mind when you interpret your results.

Method 1 - Using RooCurve::ChiSquare()

As you say the results look correct, but there is one caveat. You have a continuous model pdf (if I remember correctly, at least with a Gaussian for the background right?), and when you make the plot you have no control over how many points are sampled to make the plot. For the continuous pdf with non-vanishing second derivative, the prediction for each bin is the integral over each bin times the number of predicted events from the extended term. I don’t know exactly how you made that plot you are showing, but it seems like the continuity is lost. The RooCurve::chiSquare() function tries to estimate the integral based on the points sampled for the curve, which might be or might not be what you want (maybe your pdf is a binned pdf anyway, then it’s okay).

Method 2 - Using RooAbsPdf::createChi2()
mygiftcardsite

I think this is in the best way, but you interpreted the results wrong and also have to be careful with the parameters you pass to the createChi2 function.

First, it doesn’t divide by ndf, i.e. the number of non-zero bins minus the number of parameters. You have to do this manually afterwards, which is what you did, right? And now you are surprised why the numbers are still much larger than for method 1?

I think the problem here is how you define the uncertainty in the denominator of the chi2. By default for a Poissonian dataset, the method takes the square root of the pdf value in the bin center as the uncertainty. This is very wrong for very small predictions like you have near x = 1. Take a look at the 3rd-to last bin in the “bad” fit, I think this is what happens: your model predicts a very small value, resulting in a extremely small and wrong uncertainty prediction. However, you observe 2 events, and the residuum divided by the error makes the chi2 blow up.

Can you try changing the error definition to Poissonian confidence intervals from the data? This is what RooCurve::chiSquare() does by the way, and you can get the same uncertainty definition in createChi2 like this:

model.createChi2(hdata, Range("fullRange"),
                 Extended(true), DataError(RooAbsData::Poisson));

Note that I also added the Extended(true) command such that the prediction of the total number of events is taken from the extended pdf and not from the data. If you divide what is printed by ndf, you should get the correct result.

Still, this method doesn’t get it right if you pdf is continuous, because it just takes the pdf value in the bin center. If this is a problem for you, you can consider wrapping the pdf in a RooBinSamplingPdf, which turns the continuous pdf into a binned pdf where the values for each bin are obtained by integration.

Method 3 - Export to TH1 and use TH1::Chi2Test()

That’s an interesting approach and the results look fine, but I don’t think it’s correct. As you can see in the function documentation, the Chi2Test function is meant to compare two histograms that are both the result of a statistical process: either unweighted data or weighted Monte Carlo simulation. Your case is different, because you have a model from your fit that has no uncorrelated statistical error for each bin, like the TH1::Chi2Test assumes for both histograms.

So the values you obtain with this method seemingly look fine but are probably wrong because the test assumes that your model predictions are not the actual predictions but the result of MC from simulation around which the true predictions fluctuate. Plus you also have the binning effects mentioned before.

Method 4 - Trying to use the RooFitResult

Exactly, it’s not possible to get chi2, ndf, and pvalue of the chi2 for a RooFitResult. Fitting is separate from hypothesis testing, and the chi2 test is a form of hypothesis testing.

In conclusion, your method 2 is the recommended one, you just have to set the correct command arguments. And consider wrapping your model in a RooBinSampling pdf if it is continuous, to avoid binning effects.

Thanks for your patience and let me know if the recommendation worked for you or if you have further questions!

Cheers,
Jonas

Hello,

Thanks for step by step tutorial, I am also looking for same issue and found lots of information here, Really appreciate for help.

[astauffe]

Hi @jonas

thank you very much for your detailed answer and no worry the delay… It took me a bit of time as well to get back into it.

Firstly, regarding your starting comment: Yes, I completely agree that the chi²/ndf will only approximately follow the chi² distribution in this case. Good point.

Regarding the 4 methods… In general I am happy with your recommendation (Method 2), thanks! I was just overall very confused which method to use as there are so many (I also found the “RooChi2Var” now for example). Your comment, that in case 2 some of the very high x values would blow up the chi² was certainly also justified. However, my confusion came more from the fact that the several methods should still lead to the same result, no matter how big the chi².
As you also pointed out, in Method 2 I incorrectly interpreted the output as the chi²/ndf where it actually was just the chi². I did also try your recommendation:

model.createChi2(hdata, Range("fullRange"),
                 Extended(true), DataError(RooAbsData::Poisson));

and it looks good. However, this would of course be easier to judge if all the methods were to agree on the same values

Also, I actually did use a discrete PDF model. Yes, I started with a continuous Gaussian pdf, but for my model I actually supplied one histogram for the signal and the background separately. Where for the histogram of the gaussian template I manually integrated the pdf over the whole bin… So just as you said what RooBinSamplingPdf would do Then, to my understanding, the model it self could not have messed up the chi² depending on the method used.

So, overall I am still far away from understanding all the different methods to calculate the chi² and why some results don’t coincide. But that is fine with me. I can very well live with your recommendation of Method 2. It also naively seems to me as the most RooFit-esque way of calculating it where you can conveniently supply a range and then include the nr of fitting parameters by hand. The only downside seems to be that one has to also count the empty bins in the range oneself and then calculate the p-value indirectly.

Thank you very much for your precious help