Fitting exponential decay

[vihophong]

Hi all,
I would like to fit an exponential decay curve, which basically time difference between the time when particle decay and the time when the particle is produced. I would like to include the “negative background”, which represents random background of any events which is not correlated in time with particle production. Here is an example of such data (a histogram) generated by a simple simulation program:

My problem is that if I uses composite model with “background” and “signal”, my real “signal” function should be an exponential function which should be zero when x<0

if (x>=0.) return x0*exp(-lamda*x);
else return 0;

and the “background” function should be a zero order polynomial (pol0) :
But in Roofit I could not define such function. I guest because of the normalization condition.
Then, I choose the function as follows:

if (x>=0.) return x0*exp(-lamda*x)+C;
else return C;

Where C the constant(pol0) background.
Then I fitted the data including negative time using unbinned MLH method. In this case my PDF model contains only this function. The fit result compare to the given value of decay constant in the simulation program is not so good, and I’ve got many warnings as follows:

[#0] WARNING:Integration -- RooIntegrator1D::integral: integral of g over range (-10,10) did not converge after 20 steps
   [1] h = 1 , s = 4152.48
   [2] h = 0.25 , s = 2.37415e+06
   [3] h = 0.0625 , s = 1.18915e+06
   [4] h = 0.015625 , s = 596652

My question is: Is there any better way to define the fit function in this case?
Thank you in advance!

[ganis]

Hello,

Fitting a function with a sudden discontinuity may require some additional care.
If you are only interested in lamda, did you try to fix the value of C to, for example, the average in the negative range, and then fit for [x0, lamda} in the range [0.,2.] ?

G Ganis

[vihophong]

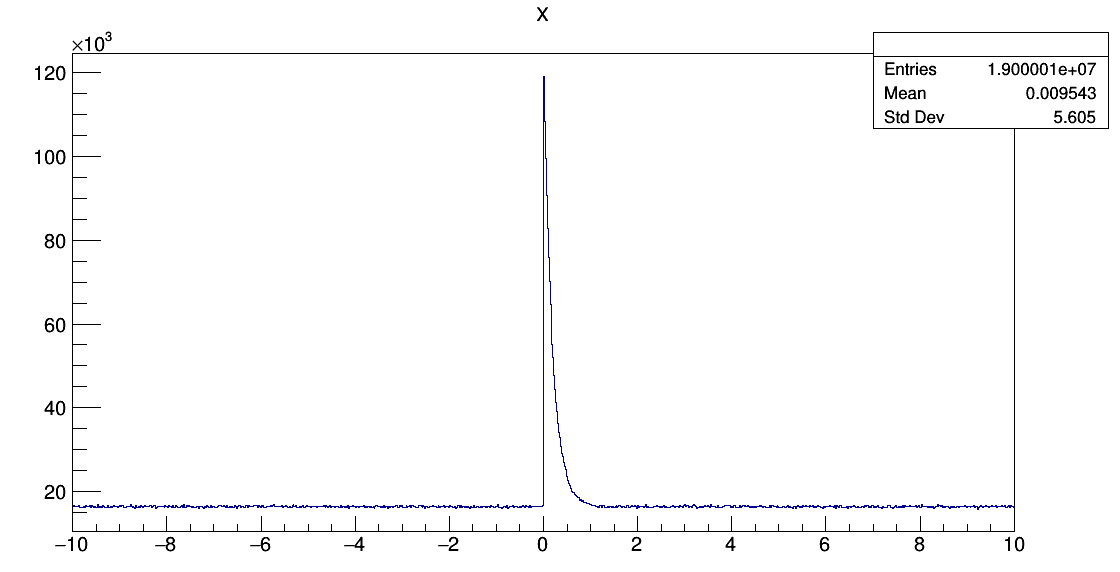
Dear Ganis,
Thank you very much for your prompt reply.

Following your suggestion, I fixed the constant background by fitting the negative range [-10,0] with a extended Polynomial model to derive mean value and error of the background. Then I used those values to constrain the background in the (extended) combined model of background and exponential functions. Here is the code:

#include "RooRealVar.h"
#include "RooDataSet.h"
#include "RooGaussian.h"
#include "RooArgSet.h"

#include "RooExponential.h"
#include "RooChebychev.h"
#include "RooPolynomial.h"
#include "RooAddPdf.h"
#include "RooExtendPdf.h"
#include "TCanvas.h"
#include "TAxis.h"
#include "RooPlot.h"
#include "TFile.h"
#include "TTree.h"
#include "fitF.cxx"
using namespace RooFit ;

void fitdev()
{
    //! parameters
    Double_t p_timerange=10.;

    Double_t p_bkgmaxerr=1000.;
    Double_t p_sigmaxerr=10000.;

    //! Input data
    TFile *f=TFile::Open("sim_mlh.root");
    TTree* tree;
    f->GetObject("treeb",tree);

    //! initial guess
    // Calculate number of backgrounds
    Double_t guessbkg=(Double_t)tree->Draw("",Form("x>%f&&x<0",-p_timerange),"goff");
    // Calculate number of signals
    Double_t guesssig=(Double_t)tree->Draw("",Form("x<%f&&x>0",p_timerange),"goff")-guessbkg;

   //! Fitting Negative background
   RooRealVar xn("x","x",-10.,0.) ;
   RooPolynomial bkgn("bkgn","bkgd negative pdf",xn);
   RooRealVar nbkgn("nbkgn","number of negative background events",guessbkg,guessbkg-p_bkgmaxerr,guessbkg+p_bkgmaxerr) ;
   RooExtendPdf ebkgn("ebkgn","extended negative background p.d.f",bkgn,nbkgn) ;
   RooDataSet* datan=new RooDataSet("data","data set",tree,xn);
   ebkgn.fitTo(*datan);
   ebkgn.Print("t") ;

   cout<<"\n\n*******Finished fitting background******* \n"<<endl;

   //! Fitting positive range
   RooRealVar x("x","x",0.,10.) ;
   RooRealVar hl("hl","half life",0.1,0.01,10.);
   RooPolynomial bkg("bkg","bkgd pdf",x);
   fitF sig("sig","sig pdf",x,hl);
   RooRealVar nsig("nsig","number of signal events",guesssig,guesssig-p_sigmaxerr,guesssig+p_sigmaxerr) ;
   RooRealVar nbkg("nbkg","number of background events",guessbkg,guessbkg-p_bkgmaxerr,guessbkg+p_bkgmaxerr) ;
   RooExtendPdf ebkg("ebkg","extended background p.d.f",bkg,nbkg) ;
   RooExtendPdf esig("esig","extended signal p.d.f",sig,nsig) ;
   RooAddPdf  model("model","(g1+g2)+a",RooArgList(ebkg,esig)) ;
   RooDataSet* data=new RooDataSet("data","data set",tree,x);

   // Fit with constrain on background derived from negative part
   RooGaussian constrlBkg("constrainBkg","constrainBkg",nbkg, RooConst(nbkgn.getVal()), RooConst(nbkgn.getError()));
   RooArgSet constrset;
   constrset.add(constrlBkg);
   model.fitTo(*data,ExternalConstraints(constrset));
   model.Print("t") ;

   //! Plotting
   RooPlot* xframe = x.frame(Title("extended ML fit example")) ;
   data->plotOn(xframe) ;
   model.plotOn(xframe,Normalization(1.0,RooAbsReal::RelativeExpected)) ;
   new TCanvas("rf202_composite","rf202_composite",600,600) ;
   gPad->SetLeftMargin(0.15) ; xframe->GetYaxis()->SetTitleOffset(1.4) ; xframe->Draw() ;
}

Where I defined the exponential function (for further developement) as follow:

/***************************************************************************** 
 * Project: RooFit                                                           * 
 *                                                                           * 
 * This code was autogenerated by RooClassFactory                            * 
 *****************************************************************************/ 

// Your description goes here... 

#include "Riostream.h" 

#include "fitF.h" 
#include "RooAbsReal.h" 
#include "RooAbsCategory.h" 
#include <math.h> 
#include "TMath.h" 

ClassImp(fitF) 

 fitF::fitF(const char *name, const char *title, 
                        RooAbsReal& _x,
                        RooAbsReal& _hl
                        ) :
   RooAbsPdf(name,title), 
   x("x","x",this,_x),
   hl("hl","hl",this,_hl)

 { 
 } 
 fitF::fitF(const fitF& other, const char* name) :  
   RooAbsPdf(other,name), 
   x("x",this,other.x),
   hl("hl",this,other.hl)
 { 
 } 
 Double_t fitF::evaluate() const 
 {
     // ENTER EXPRESSION IN TERMS OF VARIABLE ARGUMENTS HERE    
       return exp(-log(2)/hl*x);
 } 

The result is in good agreement with the value from simulation.
Do you think this method is correct?

Thank again!

Phong