Fitting ellipse to TH2F histogram ( 2D )

[iMi]

Hello,

I want to fit an elliptically shaped ring to a TH2F histogram with a function f(r,phi) that gives me the thickness of the ring as well as the semi-minor axis b - and the semi-major axis a. Cutting through the ring (the actual data) reveals a profile which is relatively flat in the middle and falls off exponentially to the inside and outside of the ring, respectively.

Ideally, I’d use two function of the form of a Fermi function substracted from each other and revolved along an ellipse.

To start with I’d like to fit a simple ellipse to the ring. Can I use the TEllipse class for this directly and if yes how?

Best.

[couet]

@iMi

Can I use the TEllipse class for this directly

No, this class is graphics only. You should provide the fitting function describing the ellipse .

[OSchaile]

Hello,
in the past (11 y) I made a macro (fitcontour.cxx) which may serve as a guide
how it could be done. There might exist more modern ways to do that meanwhile.

http://homepages.physik.uni-muenchen.de/~Otto.Schaile/macros/rootmacros.html

Cheers
Otto

[iMi]

Dear all, thanks for the suggestions.
I wrote a code in the meanwhile (see below) which does displays an elliptical annulus that falls off like a Fermi function - both to the inside and to the outside. It can be rotated and the half-axes can be changed etc.
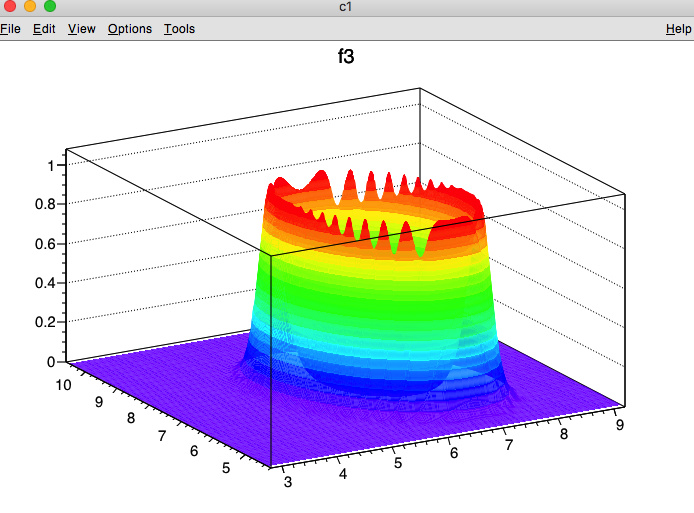
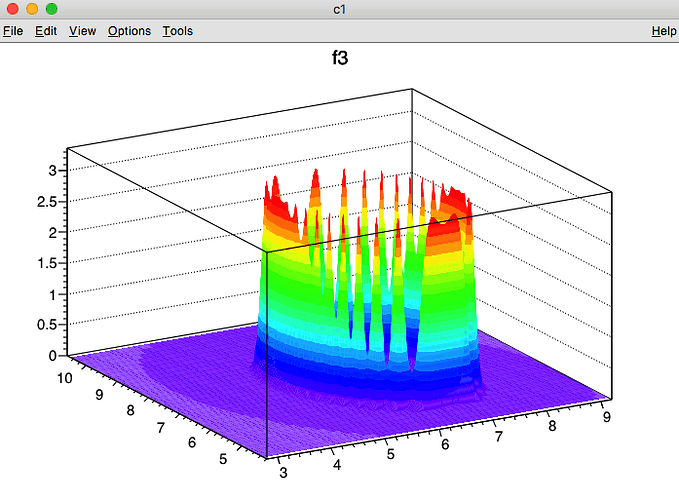
The issue that I would like to discuss with you are the oscillations on top of the rim of the elliptic annulus. If I increase the parameter that determines the steepness - the oscillations are less pronounced, see e.g;

and they become very dominant when the parameter is decreased :

Could this be an artefact?

#include “TF1.h”
#include “TF2.h”
#include “TH1.h”
#include “TH2.h”
#include “TMath.h”
#include “TEllipse.h”
#include “TStyle.h”
#include “TFile.h”
#include “TColor.h”
#include “TSpectrum.h”

// This code does the following :
// - creates a 2-D function of an annulus.
// - draws the function as a surf2 plot.
// This example can be executed via the interpreter or ACLIC
// root > .x FitAnnulus.C
// root > .x FitAnnulus.C++

Double_t g3(Double_t *x, Double_t par) {
Double_t x1 = Double_t((x[0]-par[7])cos(par[3])+(x[1]-par[8])sin(par[3]));
Double_t x2 = Double_t(-(x[0]-par[7])sin(par[3])+(x[1]-par[8])cos(par[3]));
Double_t a = Double_t(par[1]);
Double_t b = Double_t(par[2]);
Double_t r1 = Double_t((x1)(x1)/(aa));
Double_t r2 = Double_t((x2)(x2)/(bb));
Double_t A1 = Double_t((r1+r2-par[5])/par[4]);
Double_t A2 = Double_t((r1+r2-par[6])/par[4]);
return par[0](-(1/(exp(A2)+1))+1/(exp(A1)+1));
}

Double_t fun3(Double_t *x, Double_t *par) { // Both x and par are vectors.
Double_t *p1 = &par[0]; // p1 is a pointer to the address of parameter 0.
Double_t result = g3(x,p1);
return result;
}

void annulusFunc() {
gStyle->SetPalette(1);
Double_t pi = 3.14159265359;
const Int_t npar = 9;
Double_t x0 = 2.8; Double_t x1 = 9.2;
Double_t y0 = 4.2; Double_t y1 = 10.6;
TF2 f3 = new TF2(“f3”,fun3,x0,x1,y0,y1, npar);
Double_t fitPass[npar] =
{4., 1.5, 1.0, 2pi/180*60., 0.2,1.5,1.3, 6.3, 7.};
f3->SetParameters(fitPass);
f3->SetNpx(1000);
f3->Draw(“Surf2”);
}