I have problems with a custom written PDF and its integration. These problems showed up when I switched from ROOT 5.34.18 to version 6.04.02 but they are also already present with version 5.34.30.
Nothing in the changelogs gave me a clue to why this problem appeared. I am using pyROOT.
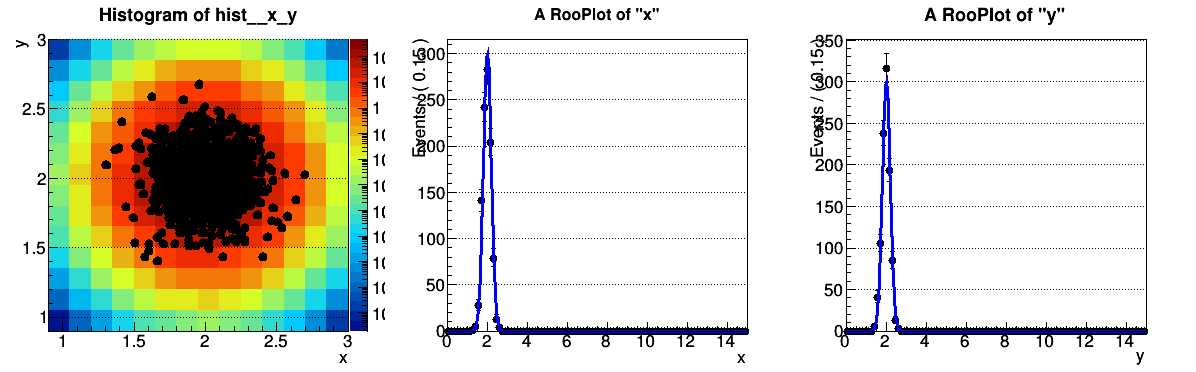
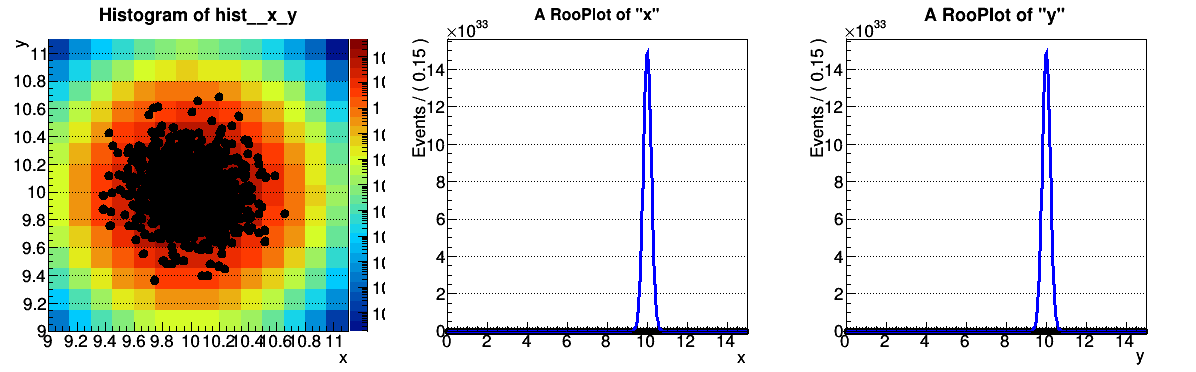
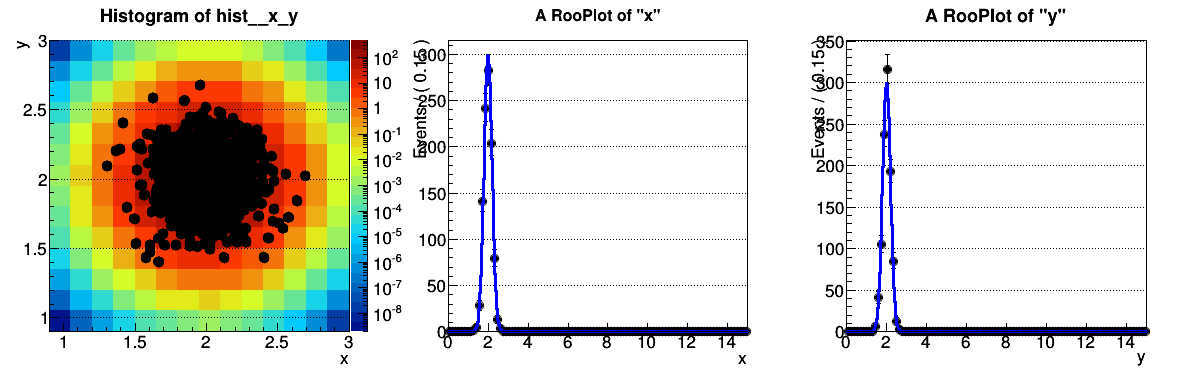
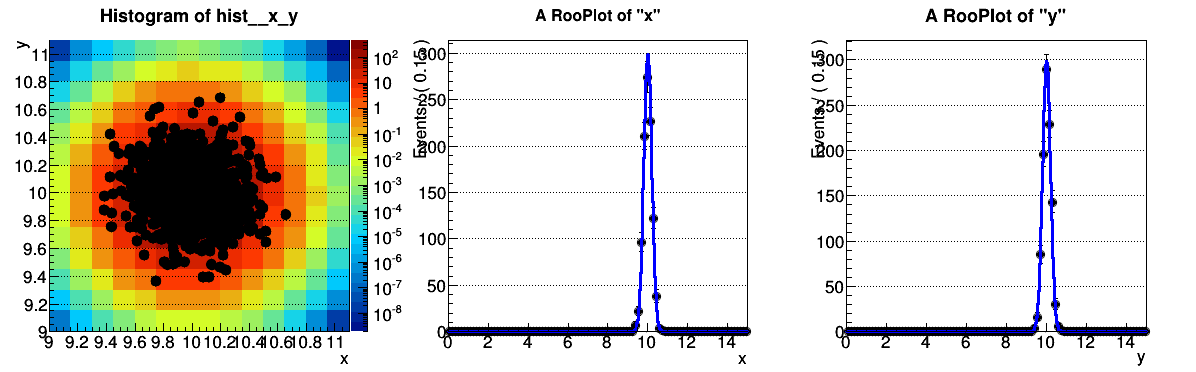
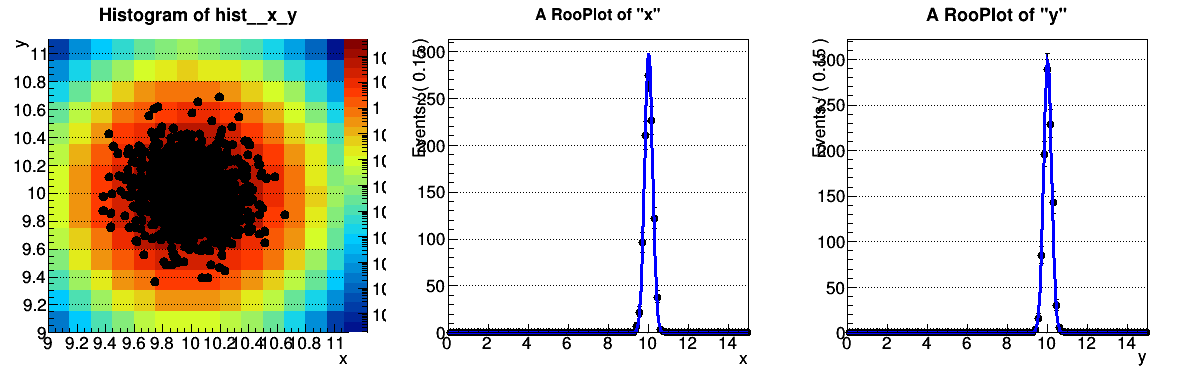
My custom PDF is a 2d Gaussian with additional features (factors to scale the center in x and y, efficiencies in both variables, input number of events to make it extended). If I plot the PDF for certain positions of the peak, the numeric integration seems to fail and thus the normalization too. I can see this in the plotted PDF and the integral I get from the expectedEvents method. With ROOT version 5.34.18 there is no problem.
It would be great if someone has an idea of why this problem shows up and how I can fix it. I would really like to do the switch to ROOT 6 but for now I’m stuck with the old version.
Here are some simple plots from the script and example results to illustrate the problem:
ROOT 5.34.30
[color=#00BF00]OK when peak @ (x=2,y=2)
inputevents = 123
integral = 123.000021457[/color]
[color=#FF0000]Problems with peak = (x=10,y=10)
inputevents = 123
integral = 2.47409635955e-30[/color]
ROOT 5.34.18
[color=#00BF00]OK when peak = (x=2,y=2)
inputevents = 123
integral = 123.000021457[/color]
[color=#00BF00]OK when peak = (x=10,y=10)
inputevents = 123
integral = 122.99999739[/color]
I attached a minimal working example in a zip-file. It contains the short python script to plot the PDF and the C++ class with the PDF description:
mwe.zip (1.98 KB)
The script does nothing more than to create fake data and plot a 2D histogram as well as the 2 projections in x and y with the fake data.
[code]#!/usr/bin/env python
import ROOT
from ROOT import RooRealVar, RooArgSet, TCanvas
RF = ROOT.RooFit
ROOT.gSystem.Load(“TestPdf_cxx.so”)
peak = 12
inputevents = 123
x = RooRealVar(“x”, “x”, 0, 15)
y = RooRealVar(“y”, “y”, 0, 15)
observables = RooArgSet(x,y)
pdf = ROOT.TestPdf(“pdf”, “pdf”, x, y, RF.RooConst(peak), RF.RooConst(0.2), RF.RooConst(0.2), RF.RooConst(1.0), RF.RooConst(1.0), RF.RooConst(1.0), RF.RooConst(1.0), RF.RooConst(inputevents))
hist = pdf.createHistogram(“hist”, x, RF.YVar(y), RF.Extended(1))
data = pdf.generate(observables, 1000)
datahist = data.createHistogram(x, y, 1500, 1500)
c1 = TCanvas(“c1”, “c1”, 1200, 400)
c1.Divide(3,1)
c1.cd(1)
c1.cd(1).SetLogz()
hist.Draw(“COLZ”)
datahist.Draw(“PSAME”)
c1.cd(2)
xframe = x.frame()
data.plotOn(xframe)
pdf.plotOn(xframe)
xframe.Draw()
c1.cd(3)
yframe = y.frame()
data.plotOn(yframe)
pdf.plotOn(yframe)
yframe.Draw()
print “inputevents =”, inputevents
print “integral =”, pdf.expectedEvents(observables)
[/code]