Dear experts,
I am trying to do an extended likelihood to a binned histogram with weights, but I am encountering issues. When comparing the negative log likelihood values of the fit to the corresponding unweighted histogram, they are much smaller which is not what they should be.
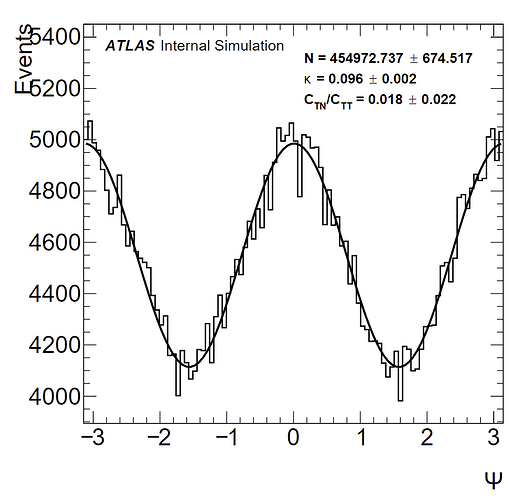
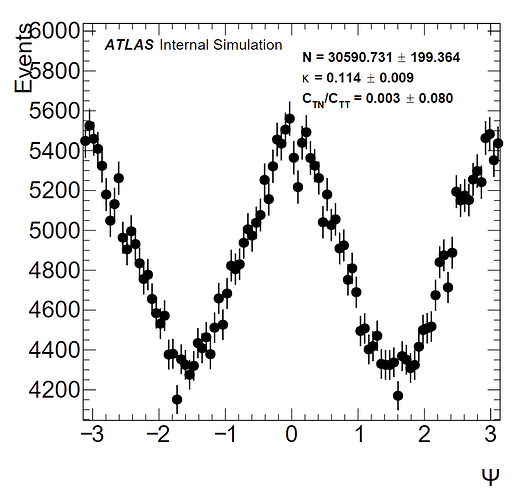
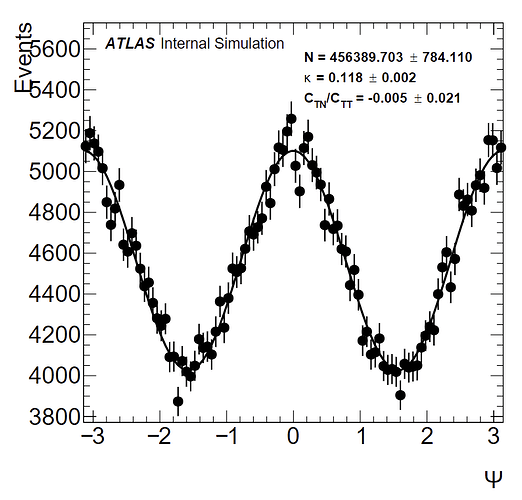
To give some background, I have a distribution from -pi to pi that is expected to follow a function of the form: a(1 + k(cos(2x) + C*sin(2x)). a is an arbitrary normalization constant; and in my fits I have let a be equal to the norm calculated by the fit divided by the number of bins (100). C_TN/C_TT is the C parameter in my fit. I have a histogram without weights, and one with weights which results in a larger amplitude (as confirmed by the kappa values I obtain). Pictures of the histograms are below:
(without weights)
(with weights)
I would like to understand why are the errors in the weighted fits so much larger than those for the unweighted fit? And also why is the norm value of the weighted fit so much smaller than what it should be? Here are snippets of my code where I perform the fitting (omega is the name I gave for the C_TN/C_TT parameter in the code):
class RooFitResultPSI(object):
def __init__(self, histogram, fit_obj, fit_function, fit_results, par_vals, par_errs):
self.fitR = fit_results
self.fit = fit_function
self.hist = histogram
self.r = fit_obj
self.pars = par_vals
self.errs = par_errs
def LL(self):
return self.fitR.minNll()
# DOES NOT WORK
# def Chi2(self):
# chi2 = 0
# for i in range(self.hist.GetNbinsX()):
# x = self.hist.GetBinCenter(i+1)
# y = self.hist.GetBinContent(i+1)
# f = self.fit.evaluate(x)
# chi2 += (y - f)**2 / f
# return chi2
def NDF(self):
return self.fitR.floatParsFinal().getSize()
def R(self):
return self.r
def Fit(self):
return self.fit
def ParVals(self):
return self.pars
def ParErrs(self):
return self.errs
def CovMatrix(self):
cov_matrix = self.fitR.covarianceMatrix()
return cov_matrix
# Extended maximum likelihood fit (unweighted)
def fitPsi_Ext(hist_psi, nEvents):
x = ROOT.RooRealVar("x", "x", -np.pi, np.pi)
kappa = ROOT.RooRealVar("kappa", "kappa", 0.1, 0, 1)
omega = ROOT.RooRealVar("omega", "omega", 0, -1, 1)
norm = ROOT.RooRealVar("norm", "norm", nEvents, 0, 2*nEvents)
psi_fit = ROOT.RooGenericPdf("psi_fit", "psi_fit", "(1 + kappa*(cos(2*x) + omega*sin(2*x)))", ROOT.RooArgList(x, kappa, omega))
psi_fit_ext = ROOT.RooExtendPdf("psi_fit_ext", "psi_fit_ext", psi_fit, norm)
data = ROOT.RooDataHist("data", "data", ROOT.RooArgList(x), hist_psi)
r = psi_fit_ext.fitTo(data, RooFit.Save())
psi_function = ROOT.TF1("psi_function", f"{norm.getVal() / hist_psi.GetNbinsX()}*(1 + {kappa.getVal()}*(cos(2*x) + {omega.getVal()}*sin(2*x)))", -np.pi, np.pi)
par_vals = [norm.getVal(), kappa.getVal(), omega.getVal()]
par_errs = [norm.getError(), kappa.getError(), omega.getError()]
fitResult = RooFitResultPSI(hist_psi, psi_fit_ext, psi_function, r, par_vals, par_errs)
return fitResult
# Extended ML fit (weighted, input histogram already has weights applied)
def fitPsi_Ext_Weight(hist_psi, nEvents):
x = ROOT.RooRealVar("x", "x", -np.pi, np.pi)
kappa = ROOT.RooRealVar("kappa", "kappa", 0.1, 0, 1)
omega = ROOT.RooRealVar("omega", "omega", 0, -1, 1)
norm = ROOT.RooRealVar("norm", "norm", nEvents, 0, 2*nEvents)
psi_fit = ROOT.RooGenericPdf("psi_fit", "psi_fit", "(1 + kappa*(cos(2*x) + omega*sin(2*x)))", ROOT.RooArgList(x, kappa, omega))
psi_fit_ext = ROOT.RooExtendPdf("psi_fit_ext", "psi_fit_ext", psi_fit, norm)
data = ROOT.RooDataHist("data", "data", ROOT.RooArgList(x), ROOT.RooFit.Import(hist_psi, True))
# data = ROOT.RooDataHist("data", "data", ROOT.RooArgList(x), hist_psi)
r = psi_fit_ext.fitTo(data, RooFit.Save(), SumW2Error=True)
# r = psi_fit_ext.fitTo(data, RooFit.Save()) # DO NOT INCLUDE SumW2Error=True
psi_function = ROOT.TF1("psi_function", f"{norm.getVal() / hist_psi.GetNbinsX()}*(1 + {kappa.getVal()}*(cos(2*x) + {omega.getVal()}*sin(2*x)))", -np.pi, np.pi)
par_vals = [norm.getVal(), kappa.getVal(), omega.getVal()]
par_errs = [norm.getError(), kappa.getError(), omega.getError()]
fitResult = RooFitResultPSI(hist_psi, psi_fit_ext, psi_function, r, par_vals, par_errs)
return fitResult
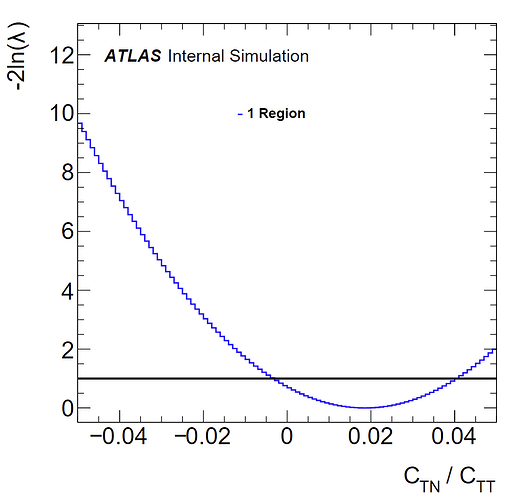
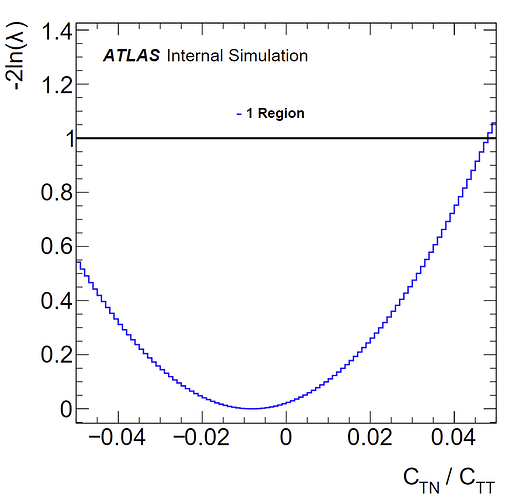
I also have negative log likelihood plots for fits to both histograms:
(unweighted)
(weighted)
If anyone could please take a look at my code and see if there are issues in how I deal with the weighted fits, I would be greatly appreciative!
Best regards,
Matt Foresi