Dear expert,
I have a histogram below.
I want to divide the bin of this histogram (may be different bin width) having about the same no of events (~2000).
Is it possible? Please help me to do this.
Regards
Chanchal
Please read tips for efficient and successful posting and posting code
ROOT Version: Not Provided
Platform: Not Provided
Compiler: Not Provided
I understand you want to divide the bin content of some of the bin by some value ?
If that concerns only “some bins”, you will need to loop over all the bins of the histogram, get the content of each of them, divide it (or not depending of your algorithm) and fill a new histogram with the new content.
Hii @couet,
Thanks for your reply.
Let me explain, what I want to do in detail.
I have two histograms in a root file (pi0_M_prefit and pi0_errM). I want to see the pi0_M_prefit in the different bins of pi0_errM which has about the same events (~2000) as you can see in the attached macro.
As you can see in the above-attached histogram which has 860032 entries. How do I decide the range of pi0_ErrM with has the same events (~2000)?
Here is the macro:
bin_histo.C (4.3 KB)
Can you please help me with that?
Regards
Chanchal
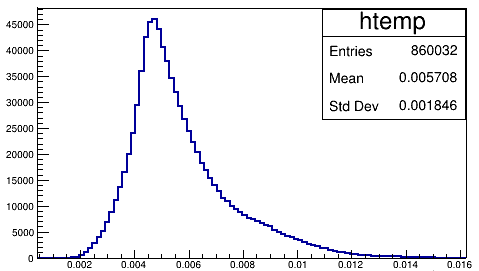
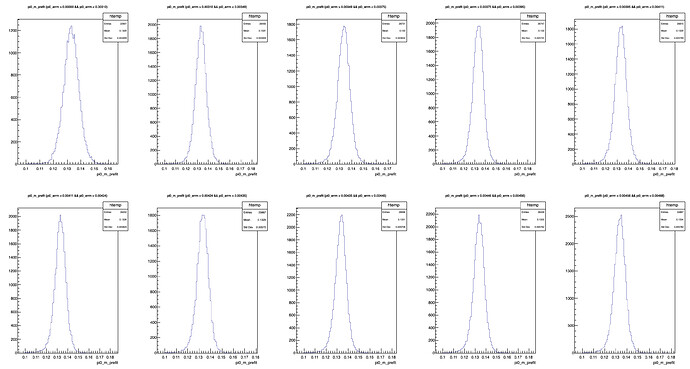
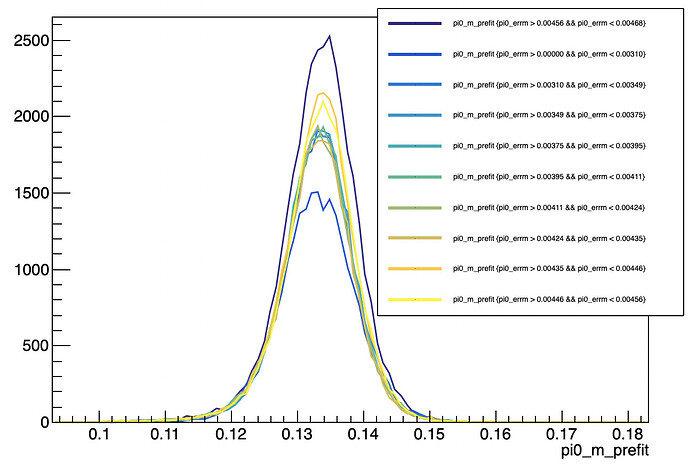
I have reorganised your macro because you were setting again and again the title of the histogram. Here is the new version:
void bin_histo() {
TFile *f = new TFile("DtoKpipi0_RS_mc14ri_a_withoutenergy.root");
TTree *tree = (TTree*)f->Get("DstD0PiKPiPi0RS_withcut");
Double_t pi0_m_prefit, pi0_errm;
tree->SetBranchAddress("pi0_m_prefit",&pi0_m_prefit);
tree->SetBranchAddress("pi0_errm",&pi0_errm);
Double_t pi0_M_PDG = 0.1349768;
TH1F *h1 = new TH1F("pi0_M_preFit_0to0.0031","",100, 0.1, 0.18);
h1->GetXaxis()->SetTitle("pi0_M_preFit [GeV/c^{2}]");
h1->GetXaxis()->SetTitleSize(0.05);
h1->GetXaxis()->CenterTitle();
TH1F *h2 = new TH1F("pi0_M_preFit_0.0031to0.00349","",100, 0.1, 0.18);
h2->GetXaxis()->SetTitle("pi0_M_preFit [GeV/c^{2}]");
h2->GetXaxis()->SetTitleSize(0.05);
h2->GetXaxis()->CenterTitle();
TH1F *h3 = new TH1F("pi0_M_preFit_0.00349to0.00375","",100, 0.1, 0.18);
h3->GetXaxis()->SetTitle("pi0_M_preFit [GeV/c^{2}]");
h3->GetXaxis()->SetTitleSize(0.05);
h3->GetXaxis()->CenterTitle();
TH1F *h4 = new TH1F("pi0_M_preFit_0.00375to0.00395","",100, 0.1, 0.18);
h4->GetXaxis()->SetTitle("pi0_M_preFit [GeV/c^{2}]");
h4->GetXaxis()->SetTitleSize(0.05);
h4->GetXaxis()->CenterTitle();
TH1F *h5 = new TH1F("pi0_M_preFit_0.00395to0.00411","",100, 0.1, 0.18);
h5->GetXaxis()->SetTitle("pi0_M_preFit [GeV/c^{2}]");
h5->GetXaxis()->SetTitleSize(0.05);
h5->GetXaxis()->CenterTitle();
TH1F *h6 = new TH1F("pi0_M_preFit_0.00411to0.00424","",100, 0.1, 0.18);
h6->GetXaxis()->SetTitle("pi0_M_preFit [GeV/c^{2}]");
h6->GetXaxis()->SetTitleSize(0.05);
h6->GetXaxis()->CenterTitle();
TH1F *h7 = new TH1F("pi0_M_preFit_0.00424to0.00435","",100, 0.1, 0.18);
h7->GetXaxis()->SetTitle("pi0_M_preFit [GeV/c^{2}]");
h7->GetXaxis()->SetTitleSize(0.05);
h7->GetXaxis()->CenterTitle();
TH1F *h8 = new TH1F("pi0_M_preFit_0.00435to0.00446","",100, 0.1, 0.18);
h8->GetXaxis()->SetTitle("pi0_M_preFit [GeV/c^{2}]");
h8->GetXaxis()->SetTitleSize(0.05);
h8->GetXaxis()->CenterTitle();
TH1F *h9 = new TH1F("pi0_M_preFit_0.00446to0.00456","",100, 0.1, 0.18);
h9->GetXaxis()->SetTitle("pi0_M_preFit [GeV/c^{2}]");
h9->GetXaxis()->SetTitleSize(0.05);
h9->GetXaxis()->CenterTitle();
TH1F *h10 = new TH1F("pi0_M_preFit_0.00456to0.00468","",100, 0.1, 0.18);
h10->GetXaxis()->SetTitle("pi0_M_preFit [GeV/c^{2}]");
h10->GetXaxis()->SetTitleSize(0.05);
h10->GetXaxis()->CenterTitle();
Int_t nentries = (Int_t)tree->GetEntries();
for (Int_t i=0; i<nentries; i++) {
tree->GetEntry(i);
if(pi0_errm > 0 && pi0_errm < 0.0031) h1->Fill(pi0_m_prefit);
if(pi0_errm > 0.0031 && pi0_errm < 0.00349) h2->Fill(pi0_m_prefit);
if(pi0_errm > 0.00349 && pi0_errm < 0.00375) h3->Fill(pi0_m_prefit);
if(pi0_errm > 0.00375 && pi0_errm < 0.00395) h4->Fill(pi0_m_prefit);
if(pi0_errm > 0.00395 && pi0_errm < 0.00411) h5->Fill(pi0_m_prefit);
if(pi0_errm > 0.00411 && pi0_errm < 0.00424) h6->Fill(pi0_m_prefit);
if(pi0_errm > 0.00424 && pi0_errm < 0.00435) h7->Fill(pi0_m_prefit);
if(pi0_errm > 0.00435 && pi0_errm < 0.00446) h8->Fill(pi0_m_prefit);
if(pi0_errm > 0.00446 && pi0_errm < 0.00456) h9->Fill(pi0_m_prefit);
if(pi0_errm > 0.00456 && pi0_errm < 0.00468) h10->Fill(pi0_m_prefit);
}
if (gROOT->IsBatch()) return;
new TBrowser();
}
So according to the value of pi0_errm you fill a different histogram. I you do not have two histograms but ten . The program you sent does not really matches with the explanations you gave.
Hi @couet,
Sorry for the confusion.
A file that I am using as input in this macro, has two branches of pi0_M_prefit and pi0_ErrM below. I could not send it here as the file size is very large.
you can find these files at the google drive link: Root Forum – Google Drive
In this macro, I am trying to see the pi0_M_prefit in the different ranges of pi0_ErrM.
I want to select this range of pi0_ErrM having the same events.
Is there any way to find this range (pi0_ErrM) which having the same events?
Regards
Chanchal
That can be easily done using TTree:Draw():
void bin_histo() {
TFile *f = new TFile("DtoKpipi0_RS_mc14ri_a_withoutenergy.root");
TTree *tree = (TTree*)f->Get("DstD0PiKPiPi0RS_withcut");
auto C = new TCanvas("C","C",1800,1000);
C->Divide(5,2);
C->cd(1); tree->Draw("pi0_m_prefit","pi0_errm > 0.00000 && pi0_errm < 0.00310");
C->cd(2); tree->Draw("pi0_m_prefit","pi0_errm > 0.00310 && pi0_errm < 0.00349");
C->cd(3); tree->Draw("pi0_m_prefit","pi0_errm > 0.00349 && pi0_errm < 0.00375");
C->cd(4); tree->Draw("pi0_m_prefit","pi0_errm > 0.00375 && pi0_errm < 0.00395");
C->cd(5); tree->Draw("pi0_m_prefit","pi0_errm > 0.00395 && pi0_errm < 0.00411");
C->cd(6); tree->Draw("pi0_m_prefit","pi0_errm > 0.00411 && pi0_errm < 0.00424");
C->cd(7); tree->Draw("pi0_m_prefit","pi0_errm > 0.00424 && pi0_errm < 0.00435");
C->cd(8); tree->Draw("pi0_m_prefit","pi0_errm > 0.00435 && pi0_errm < 0.00446");
C->cd(9); tree->Draw("pi0_m_prefit","pi0_errm > 0.00446 && pi0_errm < 0.00456");
C->cd(10); tree->Draw("pi0_m_prefit","pi0_errm > 0.00456 && pi0_errm < 0.00468");
}
It seems like you want to find a list, arraw or vector of values (bins) of pi0_errm that would contain 2000 entries, so these bins would probably not have uniform width. Since you say there are ~860k events, this means you want ~400 bins, which seems excessive and might not even be possible depending on the resolution of the data…
Anyway, I think one way would be to create the cumulative distribution in very fine bins of pi0_errm, and then just find the x value (pi0_errm) for every multiple of 2000 on y (the cumulative value).
void bin_histo() {
TFile *f = new TFile("DtoKpipi0_RS_mc14ri_a_withoutenergy.root");
TTree *tree = (TTree*)f->Get("DstD0PiKPiPi0RS_withcut");
tree->SetLineWidth(3);
auto c = new TCanvas();
tree->Draw("pi0_m_prefit","pi0_errm > 0.00456 && pi0_errm < 0.00468","L PLC");
tree->Draw("pi0_m_prefit","pi0_errm > 0.00000 && pi0_errm < 0.00310","SAME L PLC");
tree->Draw("pi0_m_prefit","pi0_errm > 0.00310 && pi0_errm < 0.00349","SAME L PLC");
tree->Draw("pi0_m_prefit","pi0_errm > 0.00349 && pi0_errm < 0.00375","SAME L PLC");
tree->Draw("pi0_m_prefit","pi0_errm > 0.00375 && pi0_errm < 0.00395","SAME L PLC");
tree->Draw("pi0_m_prefit","pi0_errm > 0.00395 && pi0_errm < 0.00411","SAME L PLC");
tree->Draw("pi0_m_prefit","pi0_errm > 0.00411 && pi0_errm < 0.00424","SAME L PLC");
tree->Draw("pi0_m_prefit","pi0_errm > 0.00424 && pi0_errm < 0.00435","SAME L PLC");
tree->Draw("pi0_m_prefit","pi0_errm > 0.00435 && pi0_errm < 0.00446","SAME L PLC");
tree->Draw("pi0_m_prefit","pi0_errm > 0.00446 && pi0_errm < 0.00456","SAME L PLC");
c->BuildLegend();
gPad->RedrawAxis();
}
Hi @dastudillo,
Yes, I want to do exactly the same.
If these are very finer bins then can we find a list of bins having ~8000 entries?
i.e divide the bins of pi0_ErrM into ~100 bins instead of 400 bins. because it’s very difficult to find these 100 bins manually at any time.
Sorry, I don’t understand what you exactly suggest to do.
Can you please explain?
Regards
Chanchal
This topic was automatically closed 14 days after the last reply. New replies are no longer allowed.
