Different shape in RooAddPdf and TF1

[yuchang]

Hi all,
I am confusing for how RooFit to do the normalization automatically for a sum of two p.d.f. . I build a sum (RooAddPdf) of two Gaussian, which means
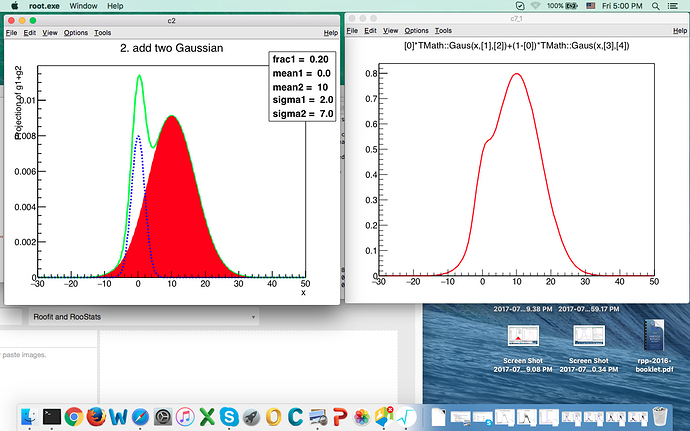
sum = 0.2 Gaus(0,2) + 0.8 Gaus(10,7)
(plot in left hand side),
and then I use ROOT TF1 to build the similar things (sum of two gaussian with fraction 0.2, 0.8, plot in right hand side). Then I expect to see the same shape despite I may not understand how the RooFit do normalization.

However, I see these two shapes are different, so I want to know how RooFit work for normalization?
And then how should I write the TF1 to make the same shape of RooFit’s case?

I provide my code in below.

// ---------------------------------------
 // for RooFit p.d.f 

  RooRealVar x("x","x",-30,30) ;
  x.setRange(-30,50); 
  x.setBins(400); 

  RooRealVar  mean1 ("mean1" ,"mean of gaussian" ,0 ,-10,10) ;
  RooRealVar  sigma1("sigma1","width of gaussian",2 ,0.1,10) ;
  RooGaussian gauss1("gauss1","gaussian PDF",x,mean1,sigma1) ;

  RooRealVar  mean2 ("mean2" ,"mean of gaussian" ,10 ,-20,20) ;
  RooRealVar  sigma2("sigma2","width of gaussian",7 ,1,30) ;
  RooGaussian gauss2("gauss2","gaussian PDF",x,mean2,sigma2) ;

  RooRealVar  frac1("frac1"  ,"frac1" , 0.2 , 0 , 1 ) ;
  RooAddPdf   sum("sum","g1+g2",RooArgList(gauss1 ,gauss2) , RooArgList(frac1));

  RooPlot* xframe2 = x.frame(Title("2. add two Gaussian")) ;

  sum.plotOn(xframe2, LineColor(kGreen)) ;
  sum.plotOn(xframe2, Components(RooArgSet(gauss2)), DrawOption("F"), FillColor(kRed)) ;
  sum.plotOn(xframe2, Components(RooArgSet(gauss1)), LineColor(kBlue), LineStyle(kDashed) ) ;

  TCanvas* c2 = new TCanvas("c2","c2",800,600) ;
  c2->cd();
  xframe2->Draw() ;

// ---------------------------------------
// for ROOT TF1

  TF1* my_func = new TF1("my_func","[0] * TMath::Gaus(x,[1],[2]) + (1-[0]) * TMath::Gaus(x,[3],[4])",-30,50);
  double my_var[5] = { 0.2, 0, 2, 10, 7 };
  my_func -> SetParameters( my_var[0] , my_var[1] , my_var[2] , my_var[3] , my_var[4] );

  TCanvas* c7_1 = new TCanvas("c7_1","c7_1",800,600) ;
  c7_1->cd(); my_func->Draw();

[moneta]

Hi

In RooFit when adding two PDF they are automatically normalised, while this is not the case for TF1.

In your particular example if you use the normalised form of the Gaussian you will get the same result:

TF1* my_func = new TF1("my_func","[0] * TMath::Gaus(x,[1],[2], true) + (1-[0]) * TMath::Gaus(x,[3],[4],true)",-30,50);

(note the boolean true passed to Math::Gaus)

In ROOT there is also a new class TF1NormSum which allows you to perform addition of normalised functions. See the tutorial example fit/fitNormSum.C

https://root.cern.ch/doc/master/fitNormSum_8C.html

Lorenzo