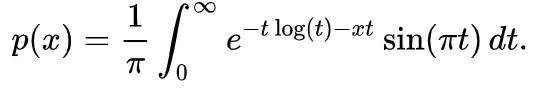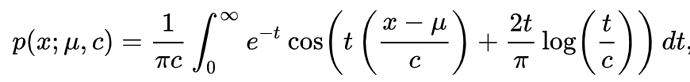Definition of Landau PDF in ROOT

[anwang]

Hi all,

I am wondering if anyone else has noticed that the Landau function in ROOT returns a different distribution than the one in Mathematica, given a location parameter and scale parameter (mu, sigma), and understands the reason.

I can only find this information about the ROOT definition:
https://root.cern.ch/root/html524/TMath.html#TMath:Landau
and that it comes from the Fortran package here:
http://cmd.inp.nsk.su/old/cmd2/manuals/cernlib/shortwrups/node151.html

For example, the ROOT documentation says that for mpv=0 and sigma=1, the MPV is at x=-0.22278.

In Mathematica, given a Landau[0,1], the maximum is at x=-0.429314.

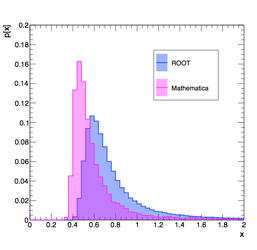
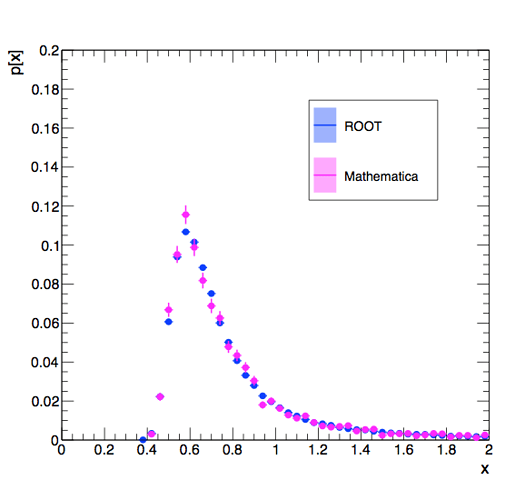
Alternatively, if I generated random events from the two programs given location parameter = 0.6, scale parameter = 0.0672, I get the following distributions which are in the image attachment…

My first thought is that the location and scale parameters are defined differently from the wikipedia version, which is what I believe Mathematica uses.

Landau distribution

Any insight would be great. Thanks!

[couet]

I think @moneta can comment on that.

[moneta]

Hello,

In ROOT we use the definition used in the CERNLIB and described in the paper that is linked from the ROOT reference documentation:
https://root.cern.ch/doc/master/group__PdfFunc.html#ga53d01e04de833eda26560c40eb207cab

and the code comes from CERNLIB, the routine you linked above in your post
The Landau is defined for a parameter lambda. Then we add just a simple transformation:
lambda = (x-m)/s and we return f (lambda)/ s where f(lambda) is the Landau density distribution described in that paper.

I am not sure exactly which definition is used by Mathematica. Do you have a link to their documentation ?

I remember wikipedia in the past was using the same definition as ROOT and it was referring the same paper, but now they have changed referring a different paper, that I could not access now.

Lorenzo

[anwang]

Hi Lorenzo,

Thanks for the information! I took a look at the paper you linked and I think I understand where the differences are now. The integral used by ROOT seems to be the second equation in wikipedia,

While the one in Mathematica seems to be the extension of the Landau distribution definition (the fourth equation in wikipedia) into a location-scale family. The documentation is here, although it’s quite sparse. But if you input that fourth equation and find the MPV, it matches the one used if you use the built in Landau function (thanks @gabrielrabanal for checking this!).

As said in wikipedia, the Mathematica version reduces to the ROOT one when mu = 0 and c = pi/2. So If i input 0 and pi/2 in Mathematica and scale the resulting random numbers by multiplying by the ROOT sigma and adding the ROOT mu, I get the same distribution.