I tried:
{
double x[4] = {8, 9, 10, 11};
//double x[4] = {18, 19, 20, 21};
//double x[4] = {28, 29, 30, 31}; // "Minuit / Migrad" FAILS
//double x[4] = {38, 39, 40, 41}; // "Minuit / Migrad" FAILS
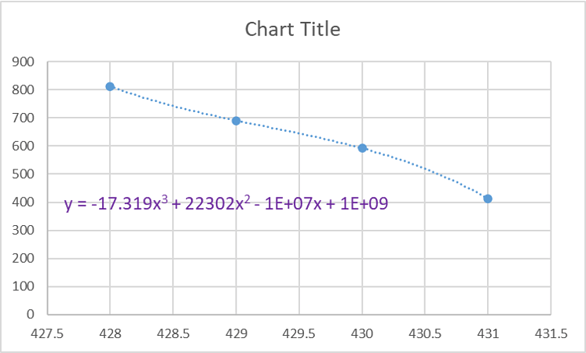
double y[4] = {813.128, 690.941, 592.383, 413.539};
TGraph *gr = new TGraph(4, x, y);
((TF1*)gROOT->GetFunction("pol3"))->SetParameters(0., 0., 0., 0.);
gr->Fit("pol3"); // Minimizer is Linear / Migrad
((TF1*)gROOT->GetFunction("pol3"))->SetParameters(0., 0., 0., 0.);
gr->Fit("pol3", "F"); // Minimizer is Minuit / Migrad
}
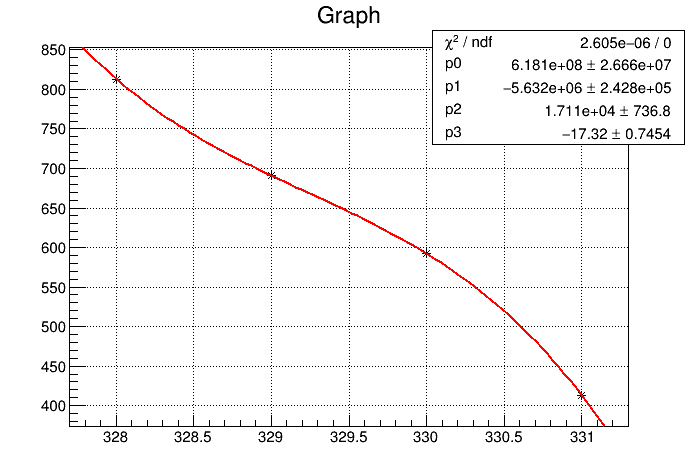
and the result is (note: the fitted parameters are equal but please compare their errors; can this be fixed somehow?):
****************************************
Minimizer is Linear / Migrad
Chi2 = 1.41398e-17
NDf = 0
p0 = 15111.1 +/- 626.132
p1 = -4514.27 +/- 200.503
p2 = 479.432 +/- 21.2485
p3 = -17.3192 +/- 0.745356
****************************************
Minimizer is Minuit / Migrad
Chi2 = 3.46746e-10
NDf = 0
Edm = 2.31219e-11
NCalls = 162
p0 = 15111.1 +/- 4.41748
p1 = -4514.27 +/- 0.695362
p2 = 479.432 +/- 0.070269
p3 = -17.3192 +/- 0.0049434
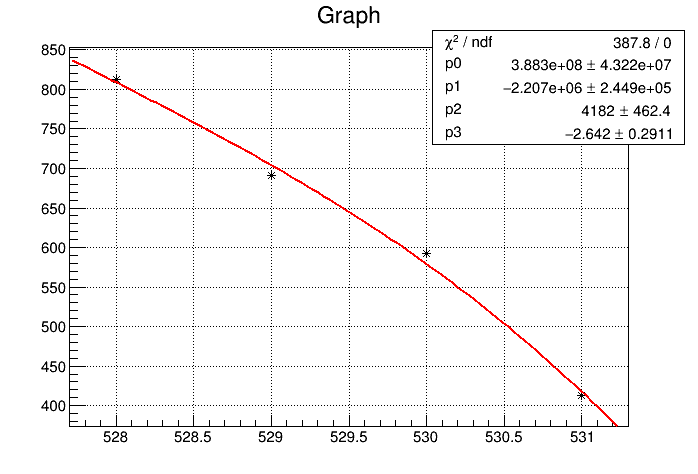
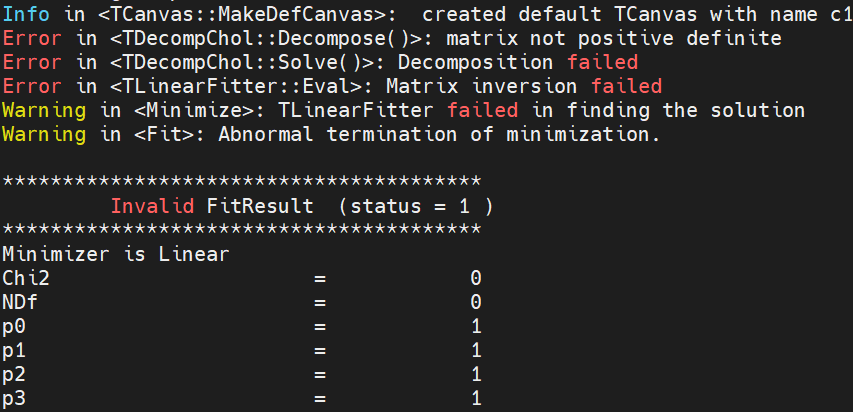
As soon as one tries “double x[4] = {28, 29, 30, 31};”, the “Minuit / Migrad” fails:
****************************************
Minimizer is Linear / Migrad
Chi2 = 6.41198e-15
NDf = 0
p0 = 435723 +/- 19094.9
p1 = -44474.6 +/- 1944.63
p2 = 1518.58 +/- 65.9659
p3 = -17.3192 +/- 0.745356
****************************************
Minimizer is Minuit / Migrad
Chi2 = 526.888
NDf = 0
Edm = 8.964e-06
NCalls = 152
p0 = -2554.59 +/- 5.37655
p1 = 162.318 +/- 0.227158
p2 = 4.40956 +/- 0.00766599
p3 = -0.211349 +/- 0.000207833
@Axel It seems to me that this simple example shows serious deficiencies of ROOT’s minimizers.