Dear all,
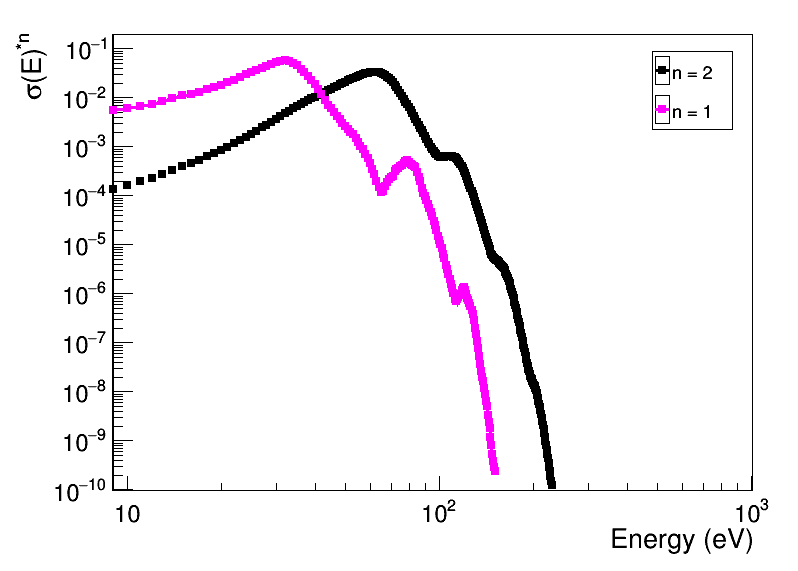
I need to perform a convolution of two TF1 I have created from a .txt data file. By creating a test (discret) convolution algorithm by myself I get the following plot (the result of the convolution of the pink one with itself is the black one):
I assume the black curve as the true curve for the convolution. Apparently, there is a class TF1Convolution.h which is supposed to give the same result. However, the result is completely different and I have no idea why. Here is the code I am using:
// c++ includes
#include <iostream>
#include <stdio.h>
#include <fstream>
// root includes
#include "TROOT.h"
#include "TRandom3.h"
#include "TTree.h"
#include "TProfile.h"
#include <TMath.h>
#include <TString.h>
#include <TFile.h>
#include <TCanvas.h>
#include <TGraph.h>
#include <TAxis.h>
#include <TF1.h>
#include <vector>
#include "TVectorD.h"
#include "TSystem.h"
#include "TLatex.h"
#include <TF1Convolution.h>
using namespace std;
// TGraph to TF1
TGraph *g1;
double myfunc(double *xx, double *)
{
return g1->Eval(xx[0]);
}
// Main function
void diego()
{
// Opening data. Here energy and PAI cross section relative to Rutherford cross section is provided
TTree *MyTree = new TTree("MyTree","MyTree");
Double_t energy, crossSection;
MyTree->ReadFile("data-Bichsel.txt","energy/D:crossSection/D");
MyTree->SetBranchAddress("energy",&energy);
MyTree->SetBranchAddress("crossSection",&crossSection);
// Probability of energy deposition
Int_t nn = MyTree->GetEntries(); // number of entries on .txt file
const Int_t n = nn;
TVectorD ene(n), Pn1(n), sigma(n), Sigma(n);
TVectorD dSigma_dE(n), dSigmaRuth_dE(n), dSigmaRuth(n);
const Double_t beta_lorentz = 0.97;
const Double_t betagamma = beta_lorentz/sqrt(1 - pow(beta_lorentz,2));
const Double_t mc2 = 0.510998928*pow(10,6);
const Double_t Emax = 2*mc2*pow(betagamma,2);
const Double_t kr = 2.54955*pow(10,-19); // constant used in Rutherford cross-section (eV.cm2)
for (int i1=0; i1<n; i1++)
{
MyTree->GetEntry(i1);
ene(i1) = energy;
sigma(i1) = crossSection;
// Rutherford cross-section
dSigmaRuth_dE(i1) = kr/pow(beta_lorentz*ene(i1),2)*(1 - pow(beta_lorentz,2)*ene(i1)/Emax);
// Converting inital cross section
Sigma(i1) = sigma(i1)*dSigmaRuth_dE(i1);
}
g1 = new TGraph(ene,Sigma);
Double_t emin = 9.203623;
Double_t emax = 94867.336;
TF1 *f1 = new TF1("f1",myfunc,emin,emax,0);
TCanvas *c1 = new TCanvas("c1","c1",800,600);
c1->cd();
gPad->SetLogx();gPad->SetLogy();
f1->Draw();
TCanvas *c2 = new TCanvas("c2","c2",800,600);
c2->cd();
TF1Convolution *f_conv = new TF1Convolution("f1","f1",true); // convolution of f1 with itself
f_conv->SetNofPointsFFT(1000);
TF1 *f = new TF1("f",*f_conv, emin, emax, f_conv->GetNpar()); // building a TF1 from the convolution
f->Draw();
}Thanks for any help,
Diego
data-Bichsel.txt (2.91 KB)
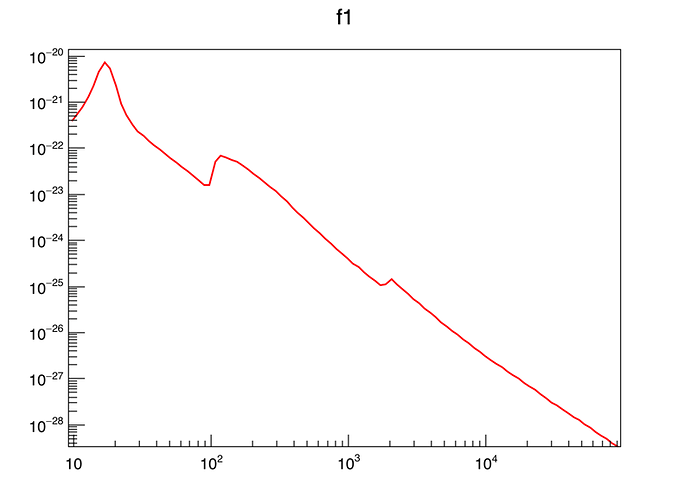
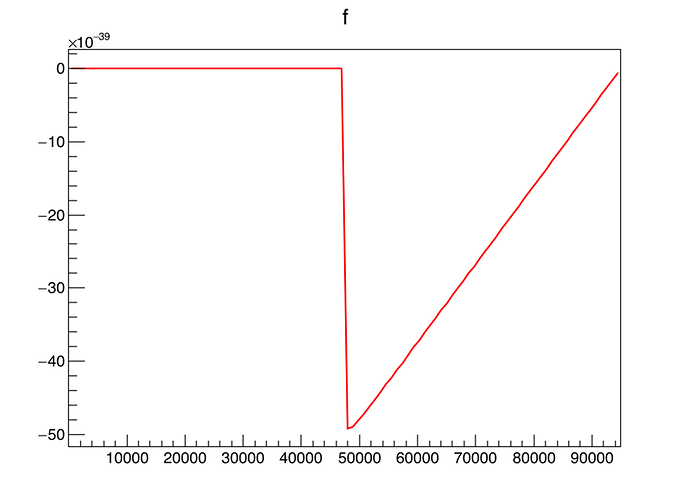

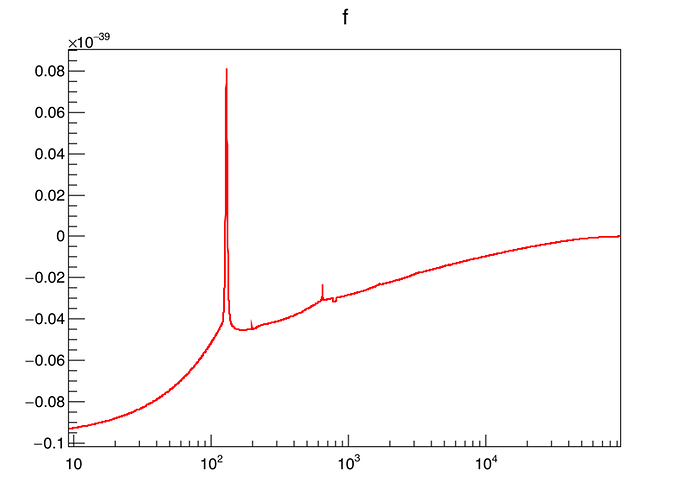

 It is necessarily wrong just by looking the original function (f1). And after modifying the integration options, nothing changes. I will go back to my own algorithm and try to make it faster.
It is necessarily wrong just by looking the original function (f1). And after modifying the integration options, nothing changes. I will go back to my own algorithm and try to make it faster.