Comparison of UL from CLs method and Bayesian approach

Roofit and RooStats
,
1

Hi, I’m estimating UL of Nsig with using model pdf(defined as Nsigsignal_pdf + Nbkgbackground_pdf).

I setted Nsig as POI and all other parameters(Nbkg and pdf shape parameters) as Nuisance parameters and used RooDataHist to estimate UL.

I tried 2 ways:

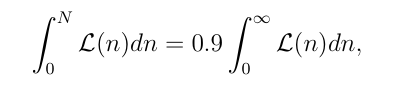
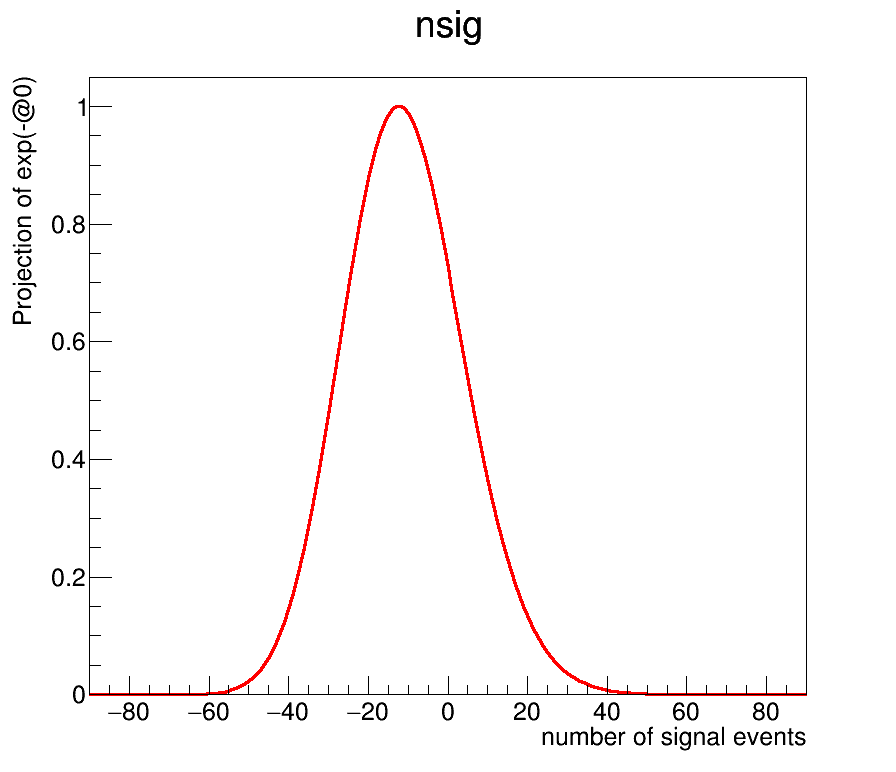
I mean I got NLL from createNLL() and createProfile() in RooStats::ProfileLikelihoodCalculator and convert this NLL to Likelihood(Nsig) by using exp(-NLL).

nsig_profileL
nsig_profileL896×772 8.07 KB

(this is Likelihood(Nsig) that I got by taking exp(-NLL))

And by calculating the fraction between integration of Likelihood(Nsig) on (0,UL of Nsig) and integration of this Likelihood(Nsig) on (0,Maximum of Nsig), I searched the smallest UL of Nsig value satisfying this fraction is greater than 0.9

And I can see the result.

If I know correctly, the CLs method is conservative way to estimate UL.

so I expected the CLs UL will be higher than bayesian UL.

But the actual result was not.

I saw the CLs UL(~16) < Bayesian UL(~20)
it seems not so big difference but slightly CLs UL is higher than Bayesian UL.

so, I would like to ask experts about this.

The CLs UL should alway higher than bayesian…?
or Is this something that happens sometimes?

Any comments and opinion about this would be helpful for me.

thanks :slight_smile:

2

Maybe related: [RF] RooStats.BayesianCalculator calculates the credibility interval on prior rather than on posterior · Issue #17567 · root-project/root · GitHub

3

Thank you for the comments,

Actually I didn’t use BayesianCalculator since the Nsig had negative value in my fit resul and in this case, the BayesianCalculator with setting SetLeftSideTailFraction(0.0) for UL had nan UL value (it seems due to my fit result is allowing negative nsig values)

So, I used ProfileLikelihoodCalculator to get NLL(Negative Log Likelihood) and used exp(-NLL) to get Likelihood function and directly integrate this Likelihood function to calculate the fraction between integration of Likelihood(Nsig) on (0,UL of Nsig) and integration of this Likelihood(Nsig) on (0,Maximum of Nsig) and search the smallest UL of Nsig value satisfying this fraction is greater than 0.9

4

Maybe @jonas has some insight

1 Like