Hi,
I’m exploring use of the RooStat package to extract asymmetry for a pair of measured yields (the actual problem is extraction of the spin asymmetry, but this simplification captures the essence of the math).
The RooStats tutorials were very helpful and I got a woking test-bed code for my simplified task.
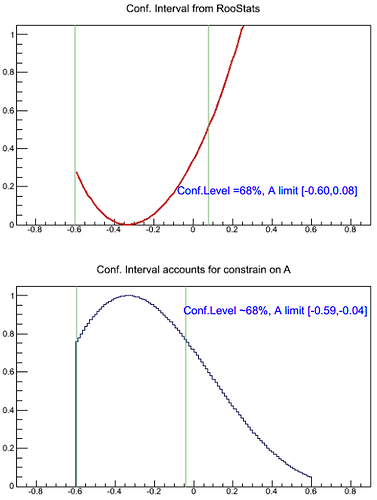
But I do not understand how the LikelihoodInterval class takes in to account the constrain on the domain of parameter of interest ?
I’m seeking advice how to overcome this issue.
Below is a short synopsis of my simplified problem, attached code works but produces result I question.
Definition of the problem:
I measure 2 independent yields n1, n2 in an experiment. Analytically I’d reconstruct the quantity: A= (n1-n2)/(n1+n2)
From independent source (physics interpretation of A) I know magnitude of A must be below some value Amax, lets say Amax=1.
In oder to apply the likelihood method using RooStats package this problem can be expressed as follows:
There are 2 parameters of the underlying model: N0,A, out of which
A is parameter of interest, N0 is the nuisance parameter.
Let variables mu1, mu2 are predictions of 2 yields based on the model:
mu1=N0(1+A)
mu2=N0(1-A)
The probability of measuring yield ‘n’ given model prediction ‘mu’ is given by the Poisson distribution f( n | mu).
The total likelihood of measuring a pair (n1,n2) is
Ltot(A,N0)=f(n1 | mu1) * f (n1 |mu2) * H( Amax - |A|)
where H(x) is the Heaviside step function.
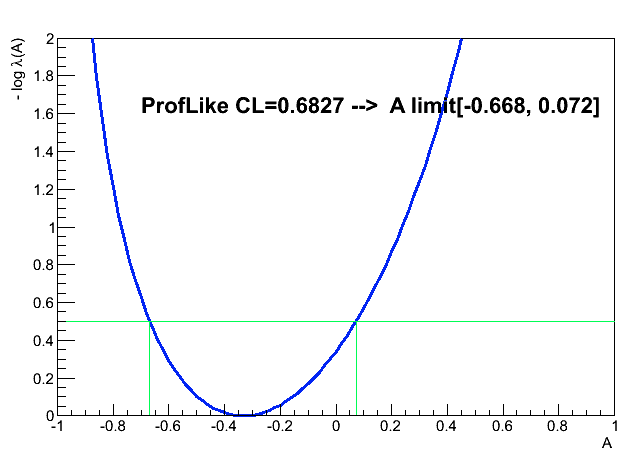
The attached macro jan_2spinAsy_constrain.C does the computation and fig 1 shows the outcome for n1=2, n2=4 (yes, very low stats), Amax=1, and CL=0.6827 the output is: limit[-0.668, 0.072].
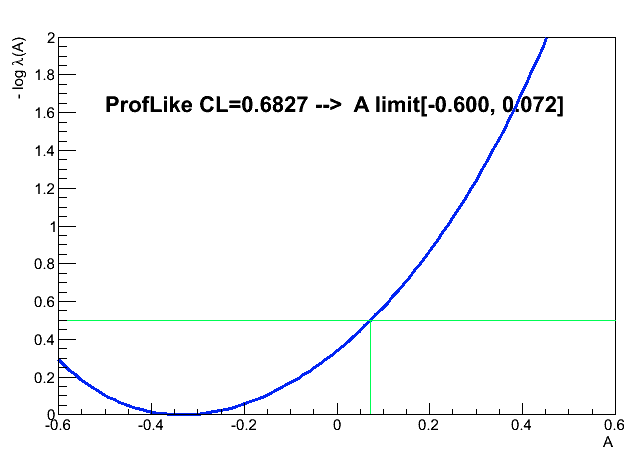
Now, I repeat extraction of A from the same pair of input yields (n1=2, n2=4 ) but under different assumption fabs(A)<0.6 (say a theorist called me and said if A >0.6 the World would never exist)
The result of ProfileLikelihoodCalculator using narrower domain for A=[-0.6,0.6] are different only on the lower limit, see Fig. 2. The upper limit of 0.072 stays unchanged.
Here is the issue:
According to CL definition, the fraction of the area below lambda(A) over confidence limit should be equal to CL. If I trim the domain of A it should be taken in to account and the upper confidence range for the same CL should move up.
Is there a way I can ask ProfileLikelihoodCalculator to include constrain |A|< Amax while returning :: GetInterval() given CL ?
Thanks
Jan
jan_2spinAsy_constrain.C (2.52 KB)