Chi2 for Landau convoluted Gauss fit

yosse_andrean · May 7, 2019, 9:14am

Dear experts,

I am fitting a distribution with Landau-Gauss conv function in Roofit and would like to calculate the chi2 value of the fit. I managed to get some value using frame.chiSquare() method, but it seems the number is questionable.
Here is the snippet of the code:

    hist = f.Get(hn)
    nbins = hist.GetSize()-2

    # Get mean and standard deviation for Gauss - Landau initial parameterization                                                                                                                                                                                                         
    mean   = hist.GetMean()
    sigma  = hist.GetStdDev()

    ## Construct observable                                                                                                                                                                                                                                                               
    minX,maxX = hist.GetXaxis().GetBinLowEdge(1), hist.GetXaxis().GetBinUpEdge(nbins)
    t = RooRealVar("t","t", minX, maxX)

    ## Construct gauss(t,mg,sg)                                                                                                                                                                                                                                                           
    mg = RooRealVar ("Gauss - mean","mg",0)
    sg = RooRealVar ("Gauss - sigma","sg",sigma,0.1*sigma,5.*sigma)
    gauss = RooGaussian ("gauss","gauss",t,mg,sg)

    ## Construct landau(t,ml,sl)                                                                                                                                                                                                                                                          
    ml = RooRealVar ("Landau - mean","mean landau",mean,mean-sigma,mean+sigma)
    sl = RooRealVar ("Landau - sigma","sigma landau",0.04,0.,0.2)
    landau = RooLandau ("lx","lx",t,ml,sl)

    ## C o n s t r u c t   c o n v o l u t i o n   p d f                                                                                                                                                                                                                                  
    ## ---------------------------------------                                                                                                                                                                                                                                            

    ## Set #bins to be used for FFT sampling                                                                                                                                                                                                                                              
    t.setBins(5000,"cache")

    ## Construct landau (x) gauss                                                                                                                                                                                                                                                         
    lxg = RooFFTConvPdf ("lxg","landau (X) gauss",t,landau,gauss)

    ## S a m p l e ,   f i t   a n d   p l o t   c o n v o l u t e d   p d f                                                                                                                                                                                                              
    ## ----------------------------------------------------------------------                                                                                                                                                                                                             

    tofit = RooDataHist("dh", "dh", RooArgList(t), hist) ;

    ## Fit lxg to data                                                                                                                                                                                                                                                                    
    lxg.fitTo(tofit);

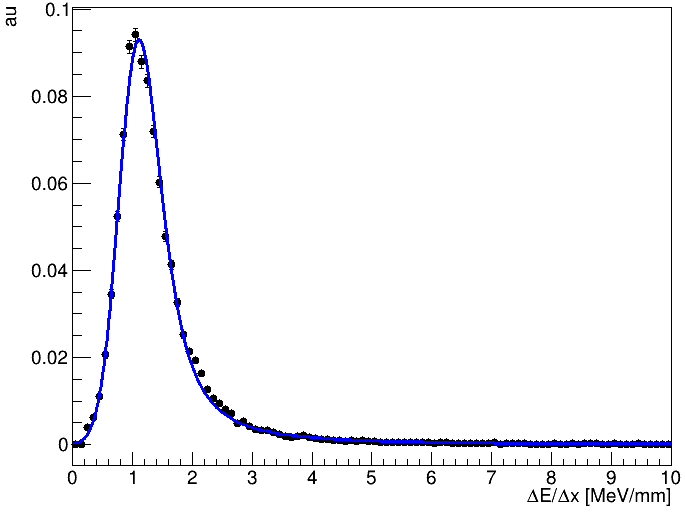
    ## Plot data, landau pdf, landau (X) gauss pdf                                                                                                                                                                                                                                        
    xframe = t.frame()
    tofit.plotOn(xframe)
    lxg.plotOn(xframe)
    xframe.GetYaxis().SetTitle('au')
    xframe.GetXaxis().SetTitle('#DeltaE/#Deltax [MeV/mm]')
    xframe.GetYaxis().SetTitleOffset(1.4)

    ## Calculate chi2                                                                                                                                                                                                                                                                     
    chi2 = xframe.chiSquare(3)
    print 'chi2 =', chi2

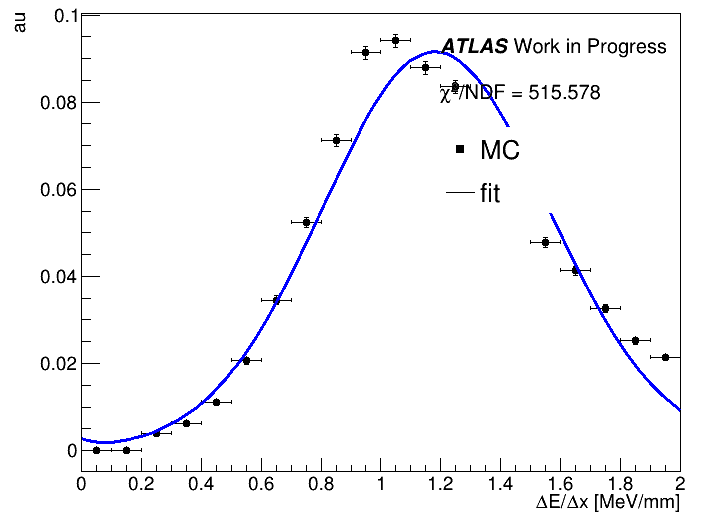
I get a result of chi2 = 17.27, which I think is too big especially when looking at the fit result below.

Note:
When calling chiSquare I use nFitParam=3 considering 3 floating parameters of the fit = Gauss - sigma, Landau - mean, Landau - sigma. Is this correct?

Best,
Yosse

StephanH · May 7, 2019, 11:19am

Hi Yosse,

at first sight, what you do looks correct, also that you have three fit parameters. For the parameters, you can still check the fit result. Use something like

result = lxg.fitTo(tofit, ROOT.RooFit.Save())
result.Print()

to have the result saved and printed. It should list only the three parameters you mentioned.
Add

lxg.paramOn(xframe)

to have the post-fit values in the plot.

What makes me think that Chi^2/ndf might actually be correct in this case is that at dE/dx = 2, the data seem to have tiny errors, but the curves don’t match. This might cause the high chi2 value.
Just to confirm, you can run the fit only from 0 to 1.8.

Is this a weighted dataset? Maybe the errors in the histogram are wrong?

yosse_andrean · May 7, 2019, 12:18pm

Hi Stephan,

For the test, if I fit from 0 to 1.8 the fit failed, I can only go to 1.9, see below. Now it gives me chi2/NDF 515,5

I’m confident that the error is correct. It comes from a weighted fill. And the histogram is later normalized.
Correct me if I’m wrong, but the error does not come in the calculation anywhere right?
https://root.cern.ch/doc/master/RooCurve_8cxx_source.html#l00545

StephanH · May 7, 2019, 1:51pm

Correction
The error of the data points is retrieved in the function you linked (although it’s being symmetrised, which is not really correct for Poisson errors). To summarise: The error of the curve is ignored, the error of the data is taken into account.

A couple more things you should try / check:

Does the histogram have SumW2 set? If not, propagation of errors will not work correctly. Many histogram operations set it automatically, but the safest option is to enable it before filling with weights. If the histogram errors are wrong, RooFit will also import the wrong errors.
Check if RooFit plots the correct data errors:
ROOT: RooAbsData Class Reference
Since the data are weighted, RooFit should automatically switch to SumW2, but it’s good to check that the errors change when manually selecting the different options using the switch DataError. If they do not change, SumW2 was probably not set in the histogram (meaning that you get sqrt(N) errors).
Could you try SumW2Error() when fitting? It should only affect the errors of the fit parameters, and not change the chi2 result, but you might check it, nevertheless.
ROOT: RooAbsPdf Class Reference
You can try a cross check:
Create a TF1 object from the post-fit PDF:
ROOT: RooAbsReal Class Reference
Use it on the original histogram for a chi2 computation:
ROOT: TH1 Class Reference
This computes Chi2 independent of RooFit. If you get similar values, the model just doesn’t fit.

yosse_andrean · May 7, 2019, 2:20pm

Hi Stephan,

Thank you for the suggestion,
Please see my replies below:

The SumW2 is set when the histogram is filled with TH1D().SetDefaultSumw2()
RooFit fit and plot the error correctly, I have made sure with

    lxg.fitTo(tofit, RooFit.SumW2Error(kTRUE));

    tofit.plotOn(xframe, RooFit.DataError(RooAbsData.SumW2))

I have made the check and the result surprises me:

    lxgtf = lxg.asTF(RooArgList(t))
    print 'chi2_tf =', hist.Chisquare(lxgtf)

I got chi2_tf = 7.64658586955e+24
So I evaluate the TF at 1.0 to see what’s going on and I get 1218447713.22. Clearly not what I expected.

Best,
Yosse

StephanH · May 7, 2019, 2:35pm

Oh, very weird. It looks like it is constructing the TF1 from unnormalised values. Does this also happen with

listWithT = ROOT.RooArgList(t)
setWithT = ROOT.RooArgSet(t)
lxg.asTF(listWithT, ROOT.RooArgSet(), setWithT)

?

yosse_andrean · May 10, 2019, 8:12am

Hi Stephan, sorry for the delay.

I think the right syntax is

lxg.asTF(ROOT.RooArgList(t), ROOT.RooArgList(), ROOT.RooArgSet(t))

But anyway, the chi2 indeed return something close to 17 (after division by NDF and normalization correction). Now I am convinced that the calculation is correct and it is the ‘knee’ of the distribution at de/dx=2.0 that causes the bad fit. Now I have to return to the drawing board to fix this.

Thanks a lot for the support,really appreciate it!

Best,
Yosse

system · May 24, 2019, 8:12am

This topic was automatically closed 14 days after the last reply. New replies are no longer allowed.