Hi and thanks for looking into this:
-
I confirm that changing the order of the arguments seems to work. OTOH it’s rather unexpected (and frustrating) that
FCONV(mips, noise)works andFCONV(noise, mips)doesn’t. I don’t think anyone can expect to not rely on convolution commutativity, though I understand computer science is not (just) mathematics. -
As for what I am trying to do it’s pretty straightforward: modelling the signal of particles passing through thin silicon detector (Landaus) with noise (Gaussian).
-
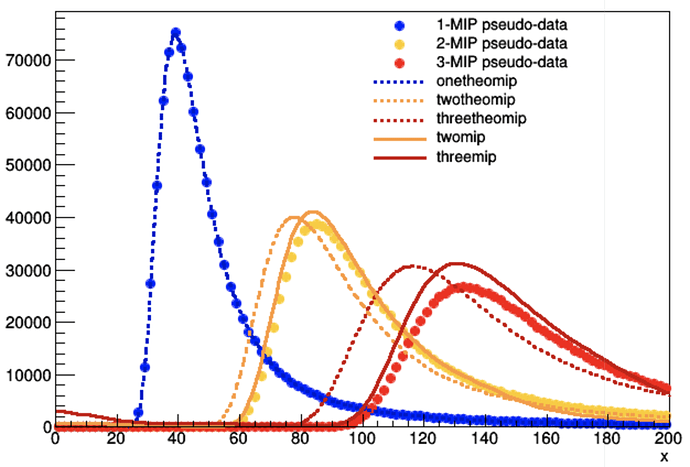
Finally, I am still puzzling as to why in ROOT/RooFit the convolution of Landau(mpv, sigma) with Landau(mpv, sigma) does not yield the same result as Landau(2mpv, 2sigma) (see also the comment above).
I looked a little more into this, tossed N pseudo-data from a Landau(mpv, sigma) and then summed pairs (or triplets) of values (data points). These are not at all described by Landau(2mpv, 2sigma) (or Landau(3mpv, 3sigma)) (dotted curves). OTOH, the convolutions of Landau(mpv, sigma) (full lines) seem to match the pseudo-data as expected (modulo some very likely numerical issues at the lowest values):
So, could the problem with dotted vs full be a numerical problem with the underlying Landau implementation? (The issues with the full lines at the lowest x values are certainly numerical…)