Hi,
I’m trying to define PDFs as a function of others in a chain, using JupyROOT 6.14/00, RooFit v3.60, and Pyhton 3.6, on OS X 10.13.6:
import ROOT as r
w = r.RooWorkspace()
onemip = w.factory('Landau::onemip(x[0,500], mpv[40,0,100], sigma_landau[5,0,20])')
twomip = w.factory('FCONV::twomip(x, onemip, onemip )')
threemip = w.factory('FCONV::threemip(x, twomip, onemip )')
threemip.getVal()
mips = w.factory('SUM::mips(fone[0.1,0,1]*onemip, ftwo[0.3,0,1]*twomip, threemip)')
mips.getVal()
noise = w.factory('Gaussian::noise(x, mu[0,-1,1], sigma_noise[2,0,20])')
noise.getVal()
signal = w.factory('FCONV::signal(x, noise, mips)')
signal.getVal()
The last getVal() seems to trigger something bad:
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-13-c4996a9ad9b2> in <module>()
----> 1 signal.getVal()
TypeError: none of the 2 overloaded methods succeeded. Full details:
double RooAbsReal::getVal(const RooArgSet* set = 0) =>
unhandled, unknown C++ exception
double RooAbsReal::getVal(const RooArgSet& set) =>
takes at least 1 arguments (0 given)[#1] INFO:Eval -- RooRealVar::setRange(x) new range named 'refrange_fft_signal' created with bounds [0,500]
[#0] ERROR:InputArguments -- RooAbsDataStore::initialize(twomip_fft_onemip_fft_CONV_onemip_fft_CACHEHIST_Obs[x_shifted_FFTBuffer2]_BufFrac0.1_BufStrat0): Data set cannot contain non-fundamental types, ignoring x_shifted_FFTBuffer2
[#0] ERROR:InputArguments -- RooHistPdf::ctor(onemip_fft_CONV_onemip_fft_CACHE_Obs[x]) ERROR histogram variable list and RooDataHist must contain the same variables.
[#0] ERROR:InputArguments -- RooAbsDataStore::initialize(twomip_fft_onemip_fft_CONV_onemip_fft_CACHEHIST_Obs[x_shifted_FFTBuffer2]_BufFrac0.1_BufStrat0): Data set cannot contain non-fundamental types, ignoring x_shifted_FFTBuffer2
[#0] ERROR:InputArguments -- RooHistPdf::ctor(onemip_fft_CONV_onemip_fft_CACHE_Obs[x]) ERROR histogram variable list and RooDataHist must contain the same variables.
Am I doing something wrong?
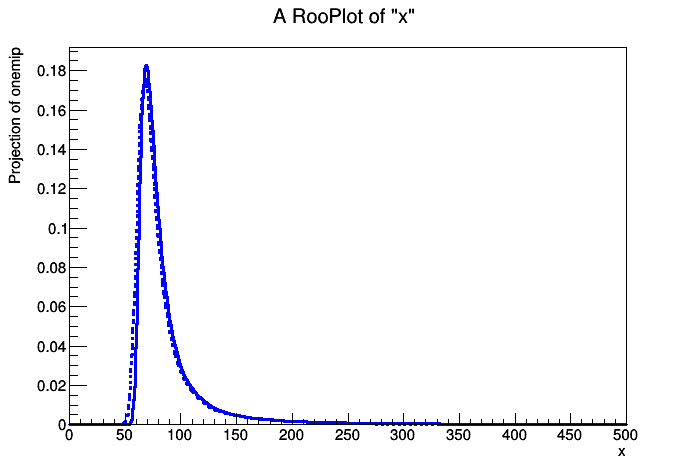
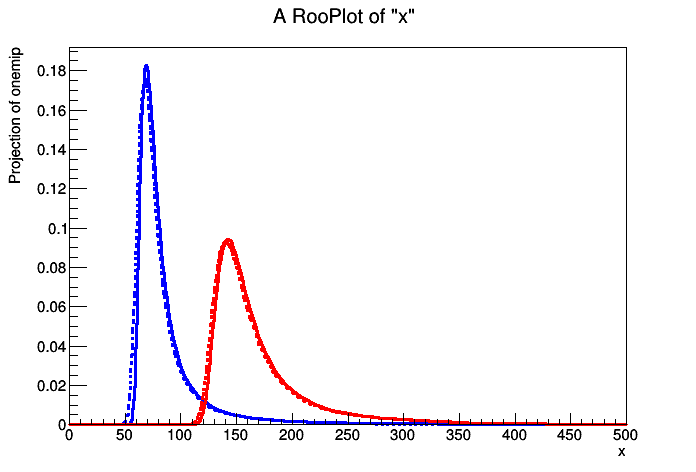
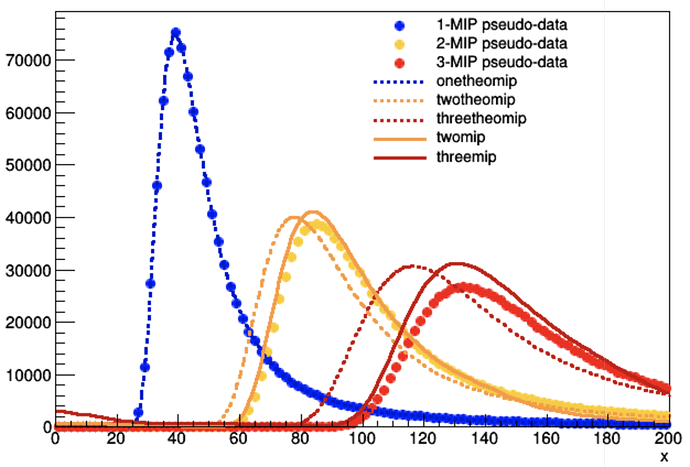

 - maybe
- maybe 