Biased estimators do not converge to the true value with a pseudo MC simulation

[chiara_iannetta]

Hello everyone,
today I’ve got a big problem concerning some manual chi-square calculation.

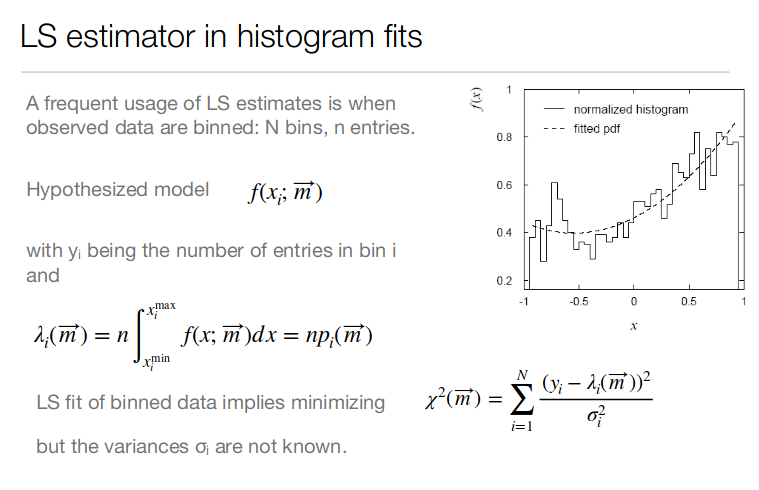
Briefly, I’m simulating muon-decay times with a double exponential + bkgr distribution:
I generate this distribution using TRandom3::GetRandom(), then I implement an algorithm to find the parameters (which I call tauPrimo and r) that minimize the Chi Square.
Obviously the challenge is not to use any ROOT feature to find the chi2 estimate.

I do 2 main loops: one on the number of events that I generate, and the other on the number of times that I calculate the min chi2.
What I want is to obtain a TH2 showing the value of one of the parameters as a function of the number of events that I have simulated. Everything works except the fact that I simulate the events with tauPrimo=0.88 and r=0.8, but the parameter estimate converges to tauPrimo=0.89 and r=0.81 as the number of events increases.

Acutally I have no clue about the nature of the bias, and here is the part of the code in which I calculate the chi2:

for (int k = 2; k <=150; k++){ 
								 
								
								x1 = h1->GetXaxis()->GetBinCenter(k);
								
								//cout<<x1<< " " << h1->GetBinWidth(k) <<endl;
								
								Mu1 = h1->GetEntries() * h1->GetBinWidth(k) * TotalDistribution(x1, alpha, tau, r1, tauPrimo1, norm1, minTime, maxTime);
								chiSquare1 += (h1->GetBinContent(k) - Mu1) * (h1->GetBinContent(k) - Mu1) / (h1->GetBinContent(k));
							}

Mu comes from this definition:

and the chi2 square expression os obtained substituting the sigma square denominator with the number of entries in the bin.
Then x1 represents the time, and total distribution is defined before as the double exponential.

I’m uploading also the .C file that I’m using right now.

Thank you so much for the help!!
Chiara

MonteCarloConsistence2.C (11.5 KB)
p.s. the number of events in the macro starts from 100000.

---

ROOT Version: 6.17
Platform: UBUNTU 18.04

---

[couet]

I cannot tell if there is something wrong in your algorithm but running your macro I can tell there is many C++ errors. For instance the variable beginTauHisto on that line is undeclared:

      TH1F *hTauPrimo = new TH1F("hTauPrimo", "#tau_{-} estimate distribution", 200, beginTauHisto, endTauHisto);

I get several like that … don’t you see them ? which root version are you using ? (16.16 does not exist).

[couet]

I also see funny code like:

                  beginRHisto1 = beginRHisto1;

Which does nothing but may suggest there is some typo …

[chiara_iannetta]

I was changing names in order to make the macro more understandable, I forgot some variables but now everything should work, sorry

[couet]

can you post the new macro ?

[chiara_iannetta]

It should have updated on the original post but here it is :
MonteCarloConsistence2.C (11.5 KB)

[couet]

What should be the two input parameters ?

[chiara_iannetta]

the first number (nExperiments) is how many times I take a distribution with x events generated and I estimate the parameters. the second number (nMaxEvents) is the maximum number of events that can be generated.

so if the first number is 10 and the second 150 000 I will estimate for 10 times the parameters on a 100 000-events distribution and I take the average of these estimates, then everything is done again on a 105 000-events distribution and so on until I reach 150 000.

edit: for each experiment, a new distribution is randomly generated (without changing the events #)

[couet]

Ok, I get this now:

root [0] .x MonteCarloConsistence2.C(10,150000)

Events = 100000
====================================
average TauPrimo= 0.907 average R= 0.827
Events = 105000
====================================
average TauPrimo= 0.8957 average R= 0.8191
Events = 110000
====================================
average TauPrimo= 0.9088 average R= 0.812
Events = 115000
====================================
average TauPrimo= 0.8864 average R= 0.812
Events = 120000
====================================
average TauPrimo= 0.8875 average R= 0.8135
Events = 125000
====================================
average TauPrimo= 0.8996 average R= 0.8283
Events = 130000
====================================
average TauPrimo= 0.8989 average R= 0.8183
Events = 135000
====================================
average TauPrimo= 0.9133 average R= 0.8313
Events = 140000
====================================
average TauPrimo= 0.9023 average R= 0.8198
Events = 145000
====================================
average TauPrimo= 0.8961 average R= 0.8221
Events = 150000
====================================
average TauPrimo= 0.8837 average R= 0.8135
..................................................................
Elapsed time in milliseconds for METHOD 2 : 6158 ms
..................................................................

May be @moneta can also have a look.

[chiara_iannetta]

In order to minimize the statistical fluctuations I have also tried to run it with (1000, 250 000). It took quite a bit to output the result, but though the result did not change. Because of the long time I’m implementing a threaded way to do it, so to use all the cores of the processor, but if anything good happens with a sample of 250 000 events I don’t know how the parallel computing can be useful

[moneta]

It is well known that the least square fit for histogram which represent counts following a Poisson distribution provides a bias estimate. You should use the maximum likelihood fit, option L when fitting Root histograms

Lorenzo

[chiara_iannetta]

But is it biased regardless of the statistics of the sample?
I was doing some research and this article clarified a little bit my issue:
“Estimators from least squares and maximum likelihood methods are often biased, even though they are consistent (converge asymptotically to the true value)”

from
[S. Baker, R. D. Cousins (1984). Clarification of the use of Chi-square and Likelihood functions in fits to histograms. Nucl.Instrum.Meth. 221 (1984) 437-442]

This would mean that with a large enough sample I should see the consistency at least…