Asymmetric errors on cluster size distributions

[MassimilianoAntonell]

Hi,
I have a question that might seem simple, but I’m unsure how to address it.
For an analysis on pixel detectors, I am extracting a histogram similar to the ones attached, focusing on the cluster size projected. This histogram represents the number of rows or columns (i.e., pixels) that my clusters have for each recorded event.

Certainly, by definition, such a distribution is strongly asymmetric since values less than 1 are not possible, and each bin represents exactly an integer value. Furthermore, as you can see from the logarithmic scale, the distribution is effectively divided into only two or three bins.

Would anyone be able to suggest a method for estimating valid asymmetric errors in this case? Clearly, the minimum cannot be less than 1. Does ROOT already have some function that takes this into account?

Thank you to anyone willing to help me out.

Best regards,
Massimiliano

[Ako_b]

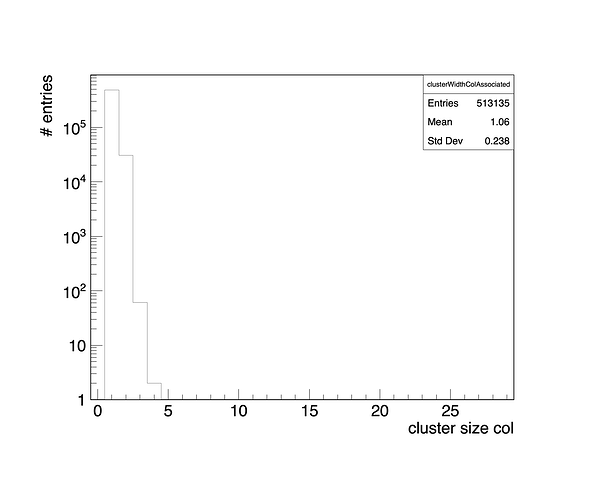
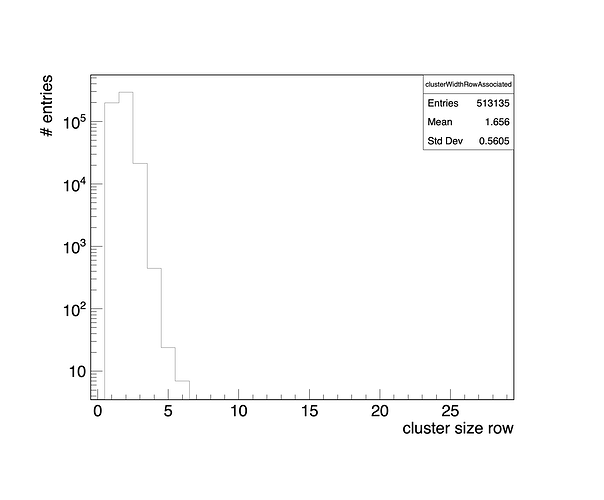
Hello, @MassimilianoAntonell !
It seems you want to somehow describe the shape of your histogram, like with a skewed normal distribution. For what parameter exactly do you want to get asymmetric errors?

Since I won’t be able to answer quickly, I’ll give my opinion for now.
I guess that you might not need asymmetric error estimation actually.
At first glance, you would probably want to check if the number of rows/columns follows a Poisson distribution using a fit. In this case, you will get symmetric errors in estimating the average number of rows/columns from the fitting, which should be valid due to the size of the event sample.
Here is a simple example, slightly adapted for your request:

// PoisFit.cpp

#include "TH1.h"
#include "TF1.h"
#include "TCanvas.h"
#include "TRandom.h"

void PoisFit() {
    // Create a histogram
    // have to shift bin edges because fitter takes function value from bin center
    // so one should keep values of discrete pdf in bin center
    double xLow = 0 - 0.5;
    double xHigh = 10 - 0.5;
    int nbins = xHigh - xLow; // right edge of the bin is excluded
    TH1D *h = new TH1D("h", "Histogram", nbins, xLow, xHigh);
    
    // Fill the histogram with random numbers following a Poisson distribution
    for (int i = 0; i < 1000; ++i) {
        h->Fill(gRandom->Poisson(1.0) + 1);
    }

    // Define a Poisson function for fitting, shift it to start from 1
    TF1 *fpois = new TF1("fpois", "[0]*TMath::Poisson(x - 1,[1])", xLow, xHigh);
    fpois->SetParameters(1, 1.0); // initial values for parameters
    fpois->SetParName(0, "nEvents");
    fpois->SetParName(1, "mean");

    // "L" option to use log-likelihood because bin content represents counts
    // "S" to save fit result, "Q" to suppress printing extra information
    TFitResultPtr fitRes = h->Fit("fpois", "LSQ");
    fitRes->Print();

    // Draw the histogram and the fitted function
    TCanvas *c1 = new TCanvas("c1", "c1", 800, 600);
    h->Draw();
    fpois->Draw("same");
}

In case you want to obtain asymmetric errors of mean estimate, you can use "E" option, which will enable MINOS [ROOT: TH1 Class Reference].

However, if your data does not follow a Poisson distribution, you will see it from the fit results. In that case you will have to conduct further research and propose a better model.

P. S.: A simple option is to calculate the skewness of the sample if that is sufficient.