Dear Georgios
Indeed, what you get this way is exactly what you read from plots that you made that are in my opinion reasonable. What I do not understand is what exactly you do not understand from your original results (at least for the lefthand plots).
It is not completely clear from your attached fe55.C file where you fill the histograms you show, because I see the fill functions commented out:
track.TransportPhoton(x0, y0, z0, t0, egamma, 0., -1.0, 0., ne);
// Fill number of electrons in ionization
// if (ne > 0) hElectrons.Fill(ne);
and
// Fill number of electrons at the pad
//if (nsum > 0) hElectrons2.Fill(nsum);
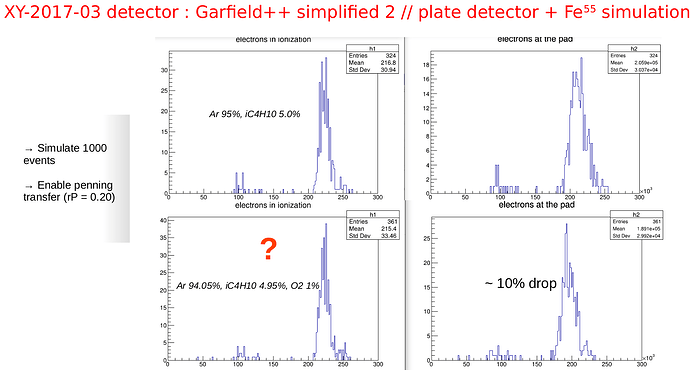
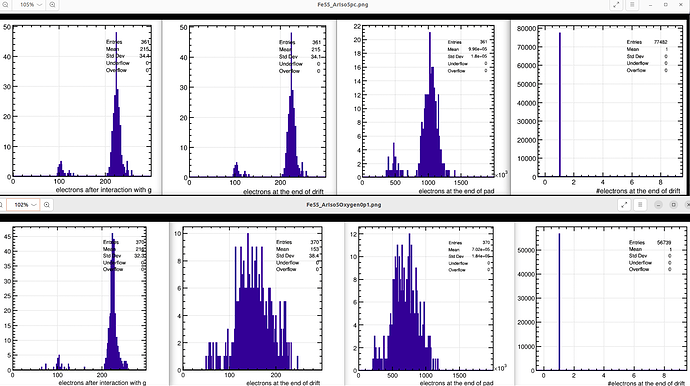
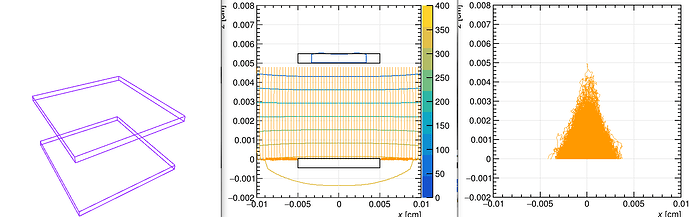
Let me for now presume these are the positions in your code that you filled those histograms. Then in this case the results (your plots) look perfectly reasonable. The leftmost plot is not the amount of electrons at the end of the drift, but is the amount of electrons directly after the interaction of the photon in the gas, calculated with heed. this is before any attachment can happen, because you are not yet simulating the transport of the ionization electrons in the gas. So it is perfectly reasonable that top and bottom plot have the same value (~215 electrons). Instead the right hand plots you fill at the end of your amplification volume and indeed you see a 10% drop, that likely is mostly due to the drift in the 1cm driftgap and not so much due to attachment in the avalanche region. If you would like to know how many electrons arrived at the end of the drift region, you should create another plot and fill the number of electrons obtained at the end of the AvalancheElectron calculation done in the driftfield:
int n_mesh = driftD.GetNumberOfElectronEndpoints();
if(n_mesh > 0) hElectrons1.Fill(n_mesh);
However, in the way you program, I believe there is something that might not be completely correct. Immagine that you drift an electron in the driftgap from position and time (x1, y1, z1, t1), but it gets attached at a certain time at a certain position (x2,y2,z2,t2). When you call the function
driftD.GetElectronEndpoint(k2, x1, y1, z1, t1, e1, x2, y2, z2, t2, e2, status);
it will get you back exactly the position (x2,y2,z2,t2) as endpoint of this electron, which is not on the boundary between the drift and the amplification volume. Instead you proceed with:
driftA.AvalancheElectron(x2, yMesh - 1e-10, z2, t2, 0, 0, 0, 0);
which means that for you it is not lost, and you place this electron in the amplification volume at same x2,z2 and at time t2, but with now with y-value such that it is inside and you run the avalanche again. This to me explains why you have always the same number of entries in histograms h1 and h2. So this in my opinion you should do in a different way (e.g. check whether the y2 value is close enough to the boundary of your driftgap).
The only thing I am a bit puzzled about is why apparently you do not have any multiplication in your amplification region. Apparently your nsum is always equal to n_mesh, which is equal to ne as explained earlier). So this you should try to find out a bit, maybe adding some couts of your driftA.GetNumberOfElectronEndpoints and/or also using the function driftA.GetAvalancheSize (neA, niA).
greets
Piet