Sorry, I had a busy week last week. I am having some email exchanges with Steve Biagi and I am still trying to understand the situation. I think I ll need a few days (and few email exchanges) more and I would like to run a few simulations before writing a wrap-up post that explains all.
Trying to explain in big lines my current understanding … the situation is the following:
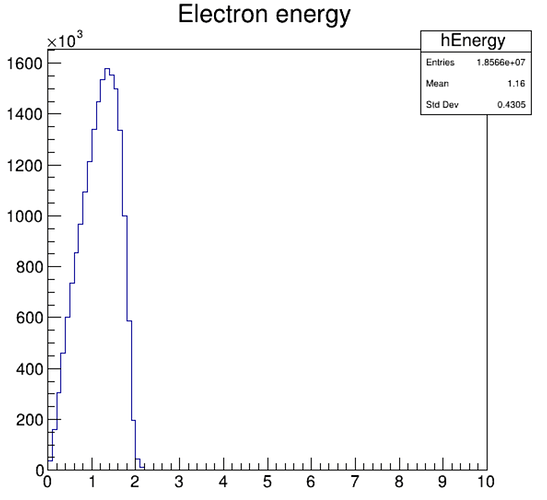
Oxygen can attach electrons both through a 2-body process (Electron Energy > 3.9eV) and 3-body process (0.05 < Electron Energy < 2 eV). I made a microscopic tracking simulation of your gas (N2:O2 80:20) for an ionization detector of 0.31cm and 1000V applied (Efield = 3.2kV/cm), and you can see clearly you don’t care about the 2-body process but only about the 3-body process:
The rate (R) of the two-body process is proportional to the (number-)density (N) of the e- attaching gas : R = kN. For the three body-process, also the N2 gas is involved and the rate is proportional to the square of the density: R = k’N(O2)N(N2). I would suggest if youo like to understand this better (and have a nice write-up in your thesis) to have a look at section 2.2.7 of Particle Detection with Drift Chambers [1], which you can lend also online from the CERN library [2,3].
Steve Biagi told me however that for the correct simulation of the 3-body process in mixtures the gasdensity must be scaled manually in magboltz and be re-compiled before using it in garfield++. From what I understood these should be the lines where action should be taken:
Now, I have not yet tried it, and I can’t guarantee that this is the only problem you have (sometimes one problem can cover another), but you have at least a starting point here.
greets
Piet
[1] Particle Detection with Drift Chambers | SpringerLink
[2] https://catalogue.library.cern/
[3] CERN Library Catalogue