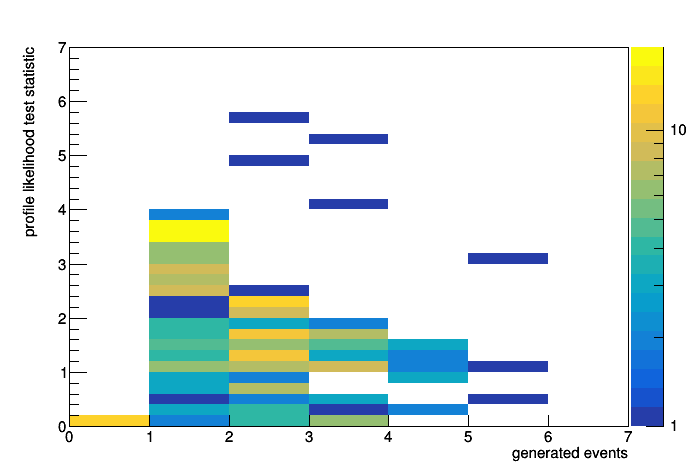
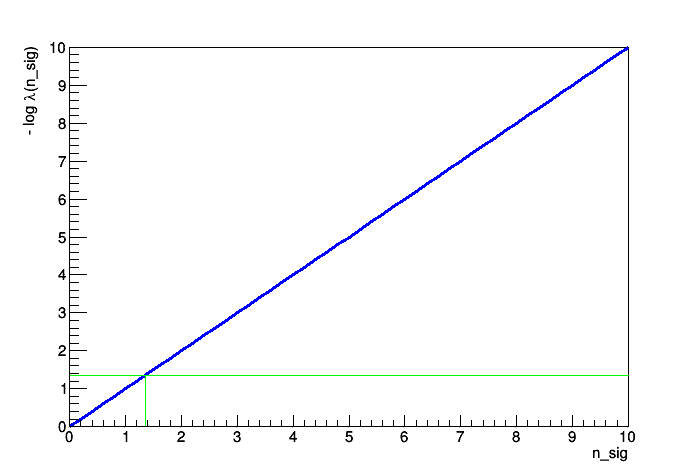
Hi Lorenzo,
thank you for the quick reply. I implemented the two lines. Unfortunately, the pointer returned by
eventstat.GetDetailedOutput()
is empty and no information is available. Looking at RooStats::TestStatistics it seems like this method is not implemented for RooStats::NumEventsTestStat:
return detailed output: for fits this can be pulls, processing time, ... The returned pointer will not loose validity until another call to Evaluate.
Reimplemented in RooStats::SimpleLikelihoodRatioTestStat, RooStats::RatioOfProfiledLikelihoodsTestStat, RooStats::ProfileLikelihoodTestStat, and RooStats::MinNLLTestStat.
UPDATE:
It did work after all. The information from the second test statistic NumEventsTestStat about how many events were generated is stored (additionally to the fit information from the ProfileLikelihoodTestStat) in the datasets which are returned by HypoTestResult::GetNullDetailedOutput() and HypoTestResult::GetAltDetailedOutput(). With this I can get easily retrieve and plot the distributions. For completeness the full code below.
Thank you very much for your help! Now I need to still find out what happens when the number of background events goes towards zero …
Lukas
#!/usr/bin/env python
import ROOT
from ROOT import RooFit as RF
from ROOT import RooStats as RS
NTOYS = 1000
# ROOT settings
ROOT.Math.MinimizerOptions.SetDefaultMinimizer('Minuit2')
# Workspace
w = ROOT.RooWorkspace('w')
# Observable
E = w.factory('E[0.,100.]')
# Constrained parameters and constraint PDF
mean = w.factory('mean[50.,49.,51.]')
mean_obs = w.factory('mean_obs[50.,49.,51.]')
mean_obs.setConstant(True)
mean_err = w.factory('mean_err[0.2]')
cpdf_mean = w.factory('Gaussian::cpdf_mean(mean,mean_obs,mean_err)')
sigma = w.factory('sigma[1.,0.5,1.5]')
sigma_obs = w.factory('sigma_obs[1.,0.5,1.5]')
sigma_obs.setConstant(True)
sigma_err = w.factory('sigma_err[0.1]')
cpdf_sigma = w.factory('Gaussian::cpdf_sigma(sigma,sigma_obs,sigma_err)')
# Signal
n_sig = w.factory('n_sig[0.,0.,10.]')
pdf_sig = w.factory('Gaussian::pdf_sig(E,mean,sigma)')
# Background
n_bkg = w.factory('n_bkg[10.,0.,50.]')
pdf_bkg = w.factory('Polynomial::pdf_bkg(E,{})')
# PDF
pdf_sum = w.factory('SUM::pdf_sum(n_sig*pdf_sig,n_bkg*pdf_bkg)')
pdf_const = w.factory('PROD::pdf_const({pdf_sum,cpdf_mean,cpdf_sigma})')
# ModelConfig
mc = RS.ModelConfig('mc', w)
mc.SetPdf( pdf_const )
mc.SetParametersOfInterest( ROOT.RooArgSet(n_sig) )
mc.SetObservables( ROOT.RooArgSet(E) )
mc.SetConstraintParameters( ROOT.RooArgSet(mean, sigma) )
mc.SetNuisanceParameters( ROOT.RooArgSet(mean, sigma, n_bkg) )
mc.SetGlobalObservables( ROOT.RooArgSet(mean_obs, sigma_obs) )
# Create toy data
data = pdf_sum.generate(ROOT.RooArgSet(E), RF.Name('data'), RF.Verbose(True), RF.Extended())
ROOT.RooAbsData.setDefaultStorageType(ROOT.RooAbsData.Vector)
data.convertToVectorStore()
# Print workspace
w.Print()
# Get RooStats ModelConfig from workspace and save it as Signal+Background model
sbModel = mc
poi = sbModel.GetParametersOfInterest().first()
poi.setVal(1.)
sbModel.SetSnapshot(ROOT.RooArgSet(poi))
# Clone S+B model, set POI to zero and set as B-Only model
bModel = mc.Clone()
bModel.SetName('mc_with_poi_0')
poi.setVal(0.)
bModel.SetSnapshot(ROOT.RooArgSet(poi))
RS.UseNLLOffset(True)
hc = RS.FrequentistCalculator(data, bModel, sbModel)
hc.SetToys(int(NTOYS), int(NTOYS/2.))
hc.StoreFitInfo(True)
hc.UseSameAltToys()
# Test statistics a: profile likelihood
profll = RS.ProfileLikelihoodTestStat(sbModel.GetPdf())
profll.EnableDetailedOutput()
profll.SetLOffset(True)
profll.SetMinimizer('Minuit2')
profll.SetOneSided(False)
profll.SetPrintLevel(0)
profll.SetStrategy(2)
profll.SetAlwaysReuseNLL(True)
profll.SetReuseNLL(True)
# Test statistics b
eventstat = RS.NumEventsTestStat(sbModel.GetPdf())
toymcs = hc.GetTestStatSampler()
toymcs.SetTestStatistic(profll,0)
toymcs.SetTestStatistic(eventstat,1)
toymcs.SetUseMultiGen(True)
# HypoTestInverter
calc = RS.HypoTestInverter(hc)
calc.SetConfidenceLevel(0.90)
calc.UseCLs(True)
calc.SetVerbose(False)
calc.SetFixedScan(6, 0., 5., False)
hypotestresult = calc.GetInterval()
# Plot HypoTestInverter result
c1 = ROOT.TCanvas()
plot = RS.HypoTestInverterPlot('hypotest_inverter', 'hypotest inverter', hypotestresult)
plot.MakePlot()
plot.MakeExpectedPlot()
plot.Draw('CLB2CL')
# Print information
hc.GetFitInfo().Print('v')
# Distribution of generated events for one hypothesis test
result = hypotestresult.GetResult(1)
h_null = ROOT.TH1I('h_null', 'generated events for null hypothesis', 50, 0, 50)
h_null.SetLineColor(ROOT.kBlue)
data_null = result.GetNullDetailedOutput()
for i in range( int(NTOYS) ):
h_null.Fill( data_null.get(i).find('mc_TS1').getVal() )
h_alt = ROOT.TH1I('h_alt', 'generated events for alt hypothesis', 50, 0, 50)
h_alt.SetLineColor(ROOT.kRed)
data_alt = result.GetAltDetailedOutput()
for i in range( int(NTOYS/2) ):
h_alt.Fill( data_alt.get(i).find('mc_with_poi_0_TS1').getVal() )
# Plot
c2 = ROOT.TCanvas()
h_null.Draw()
h_alt.Draw('SAME')