Hi,
I would like to discuss an alternative calculation of the errors in efficiency plots which I carried out recently. And I propose to exchange the current calculation implemented in ROOT with this alternative.
Here is the situation: You know there have been N0 events happening in a detector with unknown efficiency epsilon. Out of these N0 events, that detector observes N1 events (N1 <= N0). The maximum likelihood estimator for the unknown efficiency epsilon of the detector is N1/N0.
Now comes the tricky part: the uncertainty of epsilon, i.e. the confidence interval of the measurement. ROOT has a nice calculation for that since some time which uses a Bayesian approach (see TGraphAsymErrors::BayesDivide(…)). I say nice, because that approach is a correct application of Bayesian reasoning (although it answers the wrong question as I will explain later). It even turns out in this special case that the result practically agrees with the proper Frequentist calculation.
I know that because I did the latter calculation. It is follows the original Neyman construction of confidence intervals exactly which has recently been brought back to the general attention of physicists by the work of Feldman and Cousins. In fact, I mainly did this as an exercise to understand their paper.
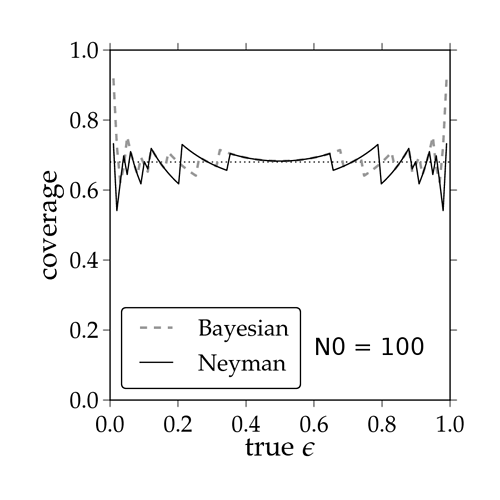
You can find the result attached (coverage.png). In that plot I show the coverage of the confidence intervals calculated by ROOT with the Bayesian approach and by the Frequentist approach for N0 = 100 as a function of the true efficency epsilon. You can see that both approaches yield the right coverage only on average. That is a natural consequence of the discreteness of the underlying statistical model, the binomial distribution. This may be hard to understand at first but is nicely explained e.g. in F. James Book: “Statistical Methods in Experimental Physics”, 2nd edition, section 9.2.2, page 227 and following.
In the following, I will not explain how the Frequentist calculation is carried out since it follows a fixed receipt exactly and there is not much to it. Instead, I will concentrate on my actual point.
I propose to replace the calculation of the Bayesian interval in ROOT with the calculation of the Frequentist interval even though both methods give almost the same results. The reason is based on philosophy and scientific strictness.
We, as scientists, want to make objective statements. The Frequentist interval has an objective interpretation: if I choose to repeat the same experiment over and over, my confidence interval covers the true value with a frequency equal to the confidence level. This property is called coverage and the Neyman construction in the Frequentist theory is based exactly on this concept.
The concept of coverage does not exist in Bayesian theory. Their intervals quantify a degree of believe. Their rules can be used, for example, to make a bet or to predict the weather or to do event classification. Their reasoning applies to single events and not to repeated events. Using Bayesian statistics to answer questions about the frequency of something to happen in a series of identical experiments is not correct.
Bottom line: Bayesian theory is beautiful, but it should be used within its intended context. In this special case, Bayesian theory happens to give the right coverage by “accident”, due to a special choice of the prior probability density function of epsilon. It gives the right answer - but to the wrong question.
Cheers,
Hans