Hi,
I am using the code attached to calculate the Wigner d-functions. I think it may be useful for other Root users(I have seem one ask for them in roottalk). The macro wig_graph.C can be used as an example on how to use the class.
Marcelo
wig_graph.C (1.67 KB)
TWignerd.cxx (5.08 KB)
TWignerd.h (1.58 KB)
Hi, I have made many improvements to the class TWignerd, some of them are:
-
I have tested its precision in performing Spherical harmonic transforms and transforms on SO(3) functions(the spherical wavelet transform)
-
Comparison with gsl associated legendre polinomials. I just checked if the are correct. But since the associated legendre polinomials are a subset of the wigner-d functions I could not test all, however the tests mentioned above are more strong.
-
Only one eighth of the coefficients are being stored(the minimum) and the others are returned by simmetry relations, with significant improvement in efficiency and performance.
There is one last simmetry that can be explored (even/odd). I was not able to use root’s FFTW wrap TVirtualFFT::SineCosine() of sine and cosine transform. This would improve performance by at least a factor of two. If anyone is willing to help me with that I would be greatefull. That would mean change TVirtualFFT::FFT() in TSmallWignerd class, by TVirtualFFT::SineCosine()(I tried with types 2 and 6, for even and odd respectively).
I think this would be a very useful tutorial on FFT’s which lacks an example of sine and cosine transforms and also useful as an option to calculate associeted legendre polinomials by FFT(and does not rely on recursion.)
If I succeed I will post again here.
The code is attached. To use it just run:
$ root load.C
root[] wig_graph(20,12,15) // for example.
Marcelo
wignerd.tar.gz (2.94 KB)
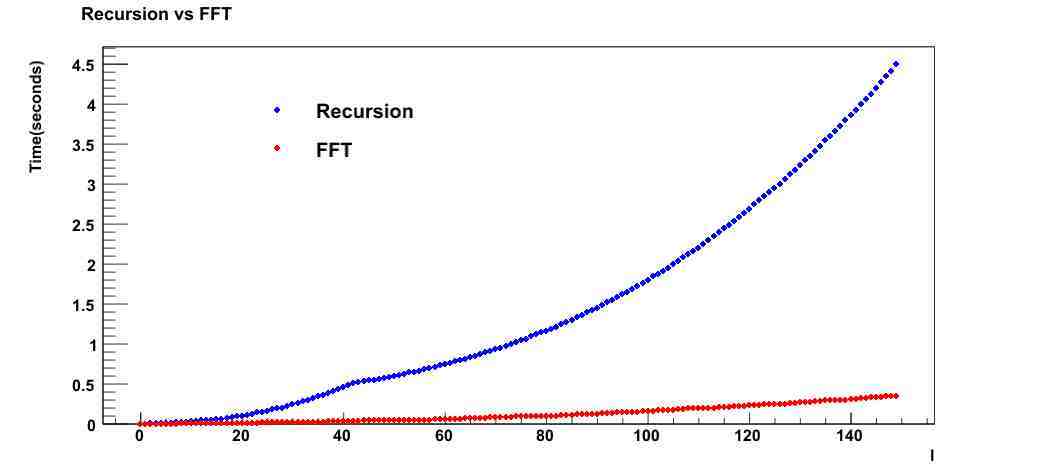
Hi, I have succeed in using sine and cosine transforms to calculate the Wigner d functions. To benchmark the code, I compared the time to calculate all associated Legendre polynomials(all l an m) up to l = 149(after that the GSL crashs). I attached a graph of the time taken for both. The code is useful as a tutorial on how to use sine and cosine transforms in ROOT. I will upload it later.
Cheers
Marcelo
Dear Root developers,
this is the last version of the code I am using to calculate the Wigner-d functions. I have seem some people interest on it, therefore I am thinking of turning it into a separate package, since at the moment it is part of my package for analysis of functions on the sphere. Is there any interest of doing it part of Root? I think this could be useful to many users including me, for example, the classes TWignerd and TSmallWignerd could be included and the macro wig_graph.C could be used as a tutorial on TVirtualFFT::SineCosine() which is lacking at the moment.
Cheers, Marcelo
wignerd.tar.gz (3.07 KB)